本文为Python算法题集之一的代码示例

题73：矩阵置零

1. 示例说明

 给定一个 m x n 的矩阵，如果一个元素为 0 ，则将其所在行和列的所有元素都设为 0 。请使用 原地 算法**。**

示例 1：

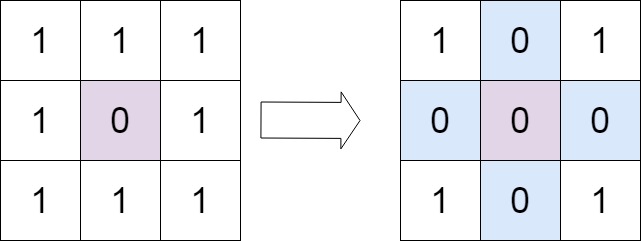
输入：matrix = [[1,1,1],[1,0,1],[1,1,1]]
输出：[[1,0,1],[0,0,0],[1,0,1]]

示例 2：

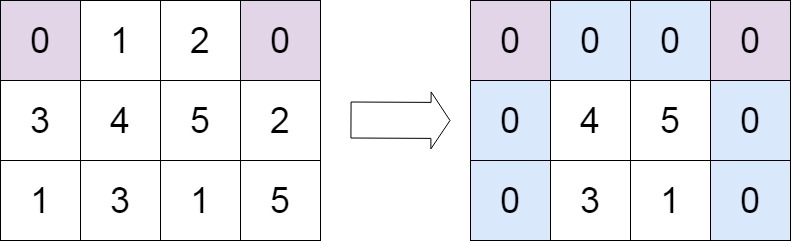
输入：matrix = [[0,1,2,0],[3,4,5,2],[1,3,1,5]]
输出：[[0,0,0,0],[0,4,5,0],[0,3,1,0]]

提示：

• m == matrix.length
• n == matrix[0].length
• 1 <= m, n <= 200
• -231 <= matrix[i][j] <= 231 - 1

进阶：

• 一个直观的解决方案是使用 O(m*n) 的额外空间，但这并不是一个好的解决方案。
• 一个简单的改进方案是使用 O(m+n) 的额外空间，但这仍然不是最好的解决方案。
• 你能想出一个仅使用常量空间的解决方案吗

---

2. 题目解析

- 题意分解

1. 原地算法是一个使用辅助的数据结构对输入进行转换的算法。它允许有少量额外的存储空间来储存辅助变量。当算法运行时，输入通常会被输出覆盖。原地算法仅通过替换或交换元素来更新输入序列。不是原地算法有时候称为非原地（not-in-place）或者不得其所（out-of-place）
2. 本题为将矩阵中的零进行行列填充
3. 本题的主要计算有2处，1是元素遍历，2是行列填充
4. 基本的解法是三层循环，读取到任何一个元素为零均进行一次行填充、一次列填充，所以基本的时间算法复杂度为O(n^3）

- 优化思路

1. 通常优化：减少循环层次

2. 通常优化：增加分支，减少计算集数量

3. 通常优化：采用内置算法来提升计算速度

4. 分析题目特点，分析最优解

   1. 必须对行列进行全扫描以确定所有0，任何一个行/列只要出现一个0就不需要再扫，可以用调度用的数据结构优化

   2. 调度用的数据可以存在输入的矩阵中，实现原地算法【空间复杂度O(1)】

---

- 测量工具

• 本地化测试说明：LeetCode网站测试运行时数据波动很大，因此需要本地化测试解决这个问题
• CheckFuncPerf（本地化函数用时和内存占用测试模块）已上传到CSDN，地址：Python算法题集_检测函数用时和内存占用的模块
• 本题很难超时，本地化超时测试用例自己生成，详见【最优算法章节】

---

3. 代码展开

1) 标准求解【三层循环】

三层循环，超过22%

丧心病狂的三层循环，可谓可算尽算，不漏过任何角落，依旧没有超时；看起来超时测试用例还是不给力

import CheckFuncPerf as cfp

def setZeroes_base(matrix):
 import copy
 matrixcopy = copy.deepcopy(matrix)
 ilenrow, ilencol = len(matrix), len(matrix[0])
 for iIdx in range(ilenrow):
     for jIdx in range(ilencol):
         if matrixcopy[iIdx][jIdx] == 0:
             for kIdx in range(ilenrow):
                 matrix[kIdx][jIdx] = 0
             for kIdx in range(ilencol):
                 matrix[iIdx][kIdx] = 0

import random
matrix = []
for iIdx in range(1000):
 matrix.append([random.randint(0,1) for x in range(1000)])
result = cfp.getTimeMemoryStr(setZeroes_base, matrix)
print(result['msg'], '执行结果 = {}'.format(result['result']))

# 运行结果
函数 setZeroes_base 的运行时间为 62147.93 ms；内存使用量为 336.00 KB 执行结果 = None

2) 改进版一【纵横计数器】

一个横向数组、一个纵向数组，检测需要置零的行列，算法相当于O(n^2) 君临天下，九九归一【超越99%】

import CheckFuncPerf as cfp

def setZeroes_ext1(matrix):
 ilenrow, ilencol = len(matrix), len(matrix[0])
 icmdrow, icmdcol = [0] * ilenrow, [0] * ilencol
 for iIdx in range(ilenrow):
     for jIdx in range(ilencol):
         if matrix[iIdx][jIdx] == 0:
             icmdrow[iIdx] = 1
             icmdcol[jIdx] = 1
 for iIdx in range(ilenrow):
     if icmdrow[iIdx] > 0:
         for jIdx in range(ilencol):
             matrix[iIdx][jIdx] = 0
 for iIdx in range(ilencol):
     if icmdcol[iIdx] > 0:
         for jIdx in range(ilenrow):
             matrix[jIdx][iIdx] = 0

import random
matrix = []
for iIdx in range(1000):
 matrix.append([random.randint(0,1) for x in range(1000)])
result = cfp.getTimeMemoryStr(setZeroes_ext1, matrix)
print(result['msg'], '执行结果 = {}'.format(result['result']))

# 运行结果
函数 setZeroes_ext1 的运行时间为 152.05 ms；内存使用量为 8.00 KB 执行结果 = None

3) 改进版二【原地算法】

在传入的矩阵中保存横向数组、纵向数组，因此空间复杂度为O(1) 表现优异，超过90%

import CheckFuncPerf as cfp

def setZeroes_ext2(matrix):
 ilenrow, ilencol = len(matrix), len(matrix[0])
 icmdrow, icmdcol = -1, -1
 bNotfind = True
 for iIdx in range(ilenrow):
     for jIdx in range(ilencol):
         if matrix[iIdx][jIdx] == 0:
             if bNotfind:
                 icmdrow = iIdx
                 icmdcol = jIdx
                 bNotfind = False
             matrix[icmdrow][jIdx] = 0
             matrix[iIdx][icmdcol] = 0
 if bNotfind:
     return
 for iIdx in range(ilenrow):
     if iIdx != icmdrow:
         if matrix[iIdx][icmdcol] == 0:
             for jIdx in range(ilencol):
                 if jIdx != icmdcol:
                     matrix[iIdx][jIdx] = 0
 for iIdx in range(ilencol):
     if iIdx != icmdcol:
         if matrix[icmdrow][iIdx] == 0:
             for jIdx in range(ilenrow):
                 if jIdx != icmdrow:
                    matrix[jIdx][iIdx] = 0
 for iIdx in range(ilenrow):
     matrix[iIdx][icmdcol] = 0
 for iIdx in range(ilencol):
     matrix[icmdrow][iIdx] = 0

import random
matrix = []
for iIdx in range(1000):
 matrix.append([random.randint(0,1) for x in range(1000)])
result = cfp.getTimeMemoryStr(setZeroes_ext2, matrix)
print(result['msg'], '执行结果 = {}'.format(result['result']))

# 运行结果
函数 setZeroes_ext2 的运行时间为 508.10 ms；内存使用量为 0.00 KB 执行结果 = None

---

4. 最优算法

根据本地日志分析，最优算法为第2种setZeroes_ext1

import random
matrix = []
for iIdx in range(1000):
    matrix.append([random.randint(0,1) for x in range(1000)])

# 算法本地速度实测比较
函数 setZeroes_base 的运行时间为 62147.93 ms；内存使用量为 336.00 KB 执行结果 = None
函数 setZeroes_ext1 的运行时间为 152.05 ms；内存使用量为 8.00 KB 执行结果 = None
函数 setZeroes_ext2 的运行时间为 508.10 ms；内存使用量为 0.00 KB 执行结果 = None

一日练，一日功，一日不练十日空

may the odds be ever in your favor ~