最小生成树介绍
最小生成树(Minimum Cost Spanning Tree)是代价最小的连通网的生成树,即该生成树上的边的权值和最小
最小生成树的性质:
必须使用且仅使用连通网中的n-1条边来联结网络中的n个顶点;
不能使用产生回路的边;
各边上的权值的总和达到最小
最小生成树在连通网场景中应用广泛,例如
在n个城市之间建立通信网络,如何建立成本最小的网络
在n个城市之间建立公路网络,如何建立成本最小的网络
应用场景:“村村通”,我国系统工程,全国行政村互通:公路、电力、生活和饮用水、电话网、有线电视网、互联网等等
村村通公路,村村通水气电,村村通5G,村村通宽带
2025年全国基本实现村村通
Prim算法
普里姆(Prim)算法设计
假设N=(V,E)是连通网
TE是N上最小生成树中边的集合
1.U={u0},(u0ÎV), TE={}
2.在所有uÎU,vÎV-U的边(u,v)ÎE中找一条代价最小的边(u,v0)并入集合TE,同时v0并入U
3.重复2,直到U=V
算法示例
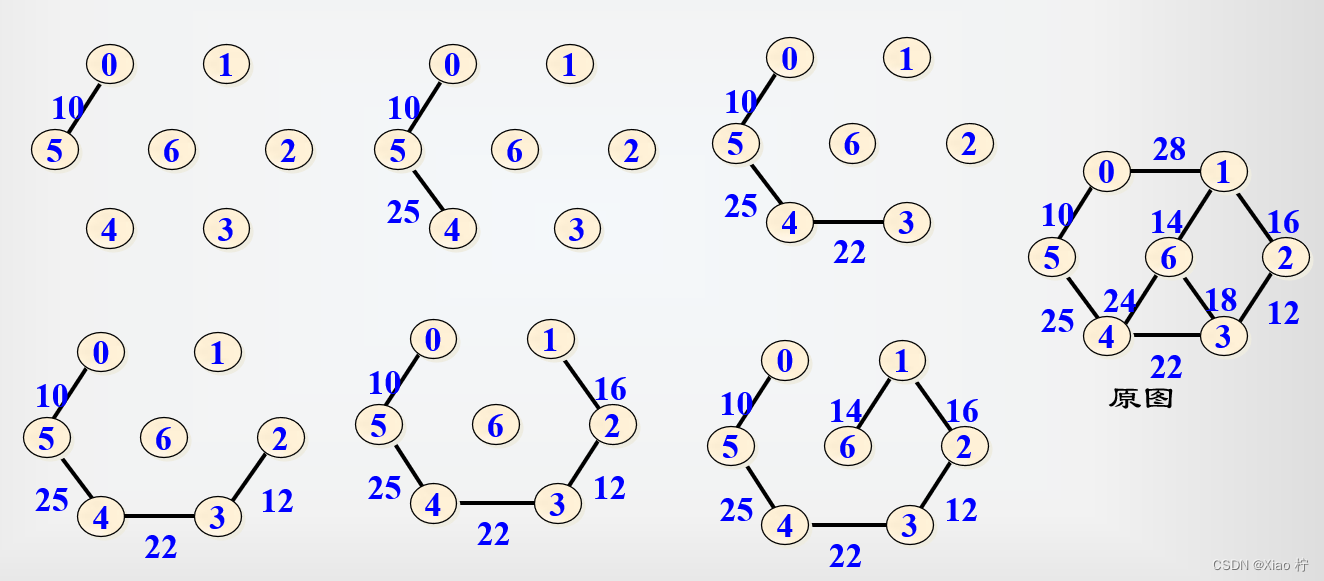
普里姆(Prim)算法设计思想:每次找到的最小权值边,一头属于已选顶点U,一头属于未选顶点V-U设置一个辅助数组closedge,用于保存未选顶点的最小权值边closedge,而且这条边的另一个点必然输入已选顶点

推导流程

普里姆(Prim)算法分析
从算法看出,算法只是和顶点数量相关,与边无关
时间复杂度为O(n2)
普里姆适用于边稠密的网,
当一个通信网的点数量少但边数量多,则用普里姆
参考设计代码
class Edge {
public:
string begin;
string end;
int weight;
};
//!!!!!!!!普里姆算法!!!!!!!!!
void Prim() {
Edge *q = new Edge[l];
string s;
cin >> s;
int start = find(s);
for (int i = 0; i < l; i++) {
arr[i][start] = 0;
}
int k = 0;
int next;
int remain = l - 1;
while (remain > 0) {
arr[start][l] = 1;
int min = 0xffff;
for (int i = 0; i < l; i++) {
if (arr[i][l] == 1) {
for (int j = 0; j < l; j++) {
if (arr[i][j] < min && arr[i][j] != 0) {
min = arr[i][j];
start = i;
next = j;
}
}
}
}
q[k].begin = str[start];
q[k].end = str[next];
q[k].weight = arr[start][next];
sum += arr[start][next];
k++;
for (int i = 0; i < l; i++) {
arr[i][next] = 0;
}
remain--;
start = next;
}
cout << sum << endl;
cout << "prim:" << endl;
for (int i = 0; i < k; i++)
cout << q[i].begin << ' ' << q[i].end << ' ' << q[i].weight << endl;
}
Kruskal算法
最小生成树生成算法——克鲁斯卡尔(Kruskal)算法
假设G=(V,E)是连通网,设非连通图T={V,{}},图中每个顶点自成一个连通分量
1.在E中找一条代价最小,且其两个顶点分别依附不同的连通分量的边,将其加入T中
2.重复1,直到T中所有顶点都在同一连通分量上
算法示例
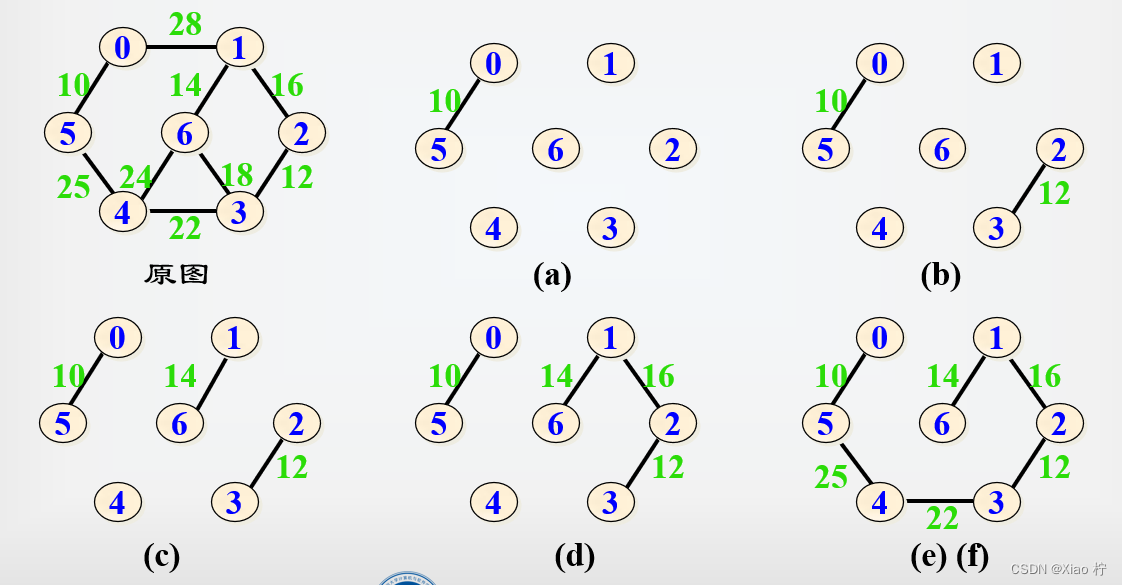
算法设计
克鲁斯卡尔算法设计用选择排序算法,只需要即找出n-1条符合要求的边
难点:如何判断一条边属于两个不同的连通分量
设计辅助数组Belong[n],其中Belong[i]初始为-1,表示顶点i未选
当选中一条边,查看这条边的两个顶点i和j
如果Belong[i]和Belong[j]都是-1,则生成新分量编号并设Belong[i]和Belong[j]
如果Belong[i]或Belong[j]是-1,则生成新分量编号并设Belong[i]或Belong[j]
如果Belong[i]或Belong[j]都不是-1,则说明两个顶点已选
如果Belong[i]==Belong[j],则说明同属一个分量,放弃
如果Belong[i]<>Belong[j],则说明分属不同分量,选择这条边并把两个分量合并,即更改相关分量的Belong值
算法分析
算法只是和边数量相关,因此适用于点稠密的网
时间复杂度为O(eloge)
当一个通信网的边数量少但点数量多,则适用
参考代码
//克鲁斯卡尔算法执行结点
class edge {
public:
int begin;
int end;
int weight;
};
//!!!!!!!克鲁斯卡尔算法!!!!!
void Kurskal() {
for (int i = 0; i < l; i++)
flag[i] = 0;
cout << "kruskal:" << endl;
//将所获得边集数组进行排序
for (int i = 0; i < t; i++)
for (int j = 0; j < t - i - 1; j++) {
if (e[j].weight > e[j + 1].weight)
swap(e[j], e[j + 1]);
}
for (int i = 0; i < l; i++) {
int o = find(e[i].begin);
int p = find(e[i].end);
if (o != p) {
flag[o] = p;
cout << str[e[i].begin] << ' ' << str[e[i].end] << ' ' << e[i].weight << endl;
}
}
}
完整代码(仅供参考)
#include<iostream>
#include<queue>
#define nu 0xffff;
using namespace std;
class node {
public:
int info;
node *next;
node() {
next = nullptr;
}
};
class point {
public:
int data;
node *head;
point() {
head = nullptr;
}
};
//克鲁斯卡尔算法执行结点
class edge {
public:
int begin;
int end;
int weight;
};
class Edge {
public:
string begin;
string end;
int weight;
};
class graph {
private:
int l, t;
int **arr;
string *str;
int *flag;
edge *e;
int sum = 0;
point *a;
int n, m;
public:
graph() {
Create();
}
//邻接矩阵存储
void Create() {
cin >> l;
str = new string[l];
flag = new int[l];
arr = new int *[l + 1];
for (int i = 0; i < l; i++) {
flag[i] = 0;
arr[i] = new int[l];
}
for (int i = 0; i < l; i++)
for (int j = 0; j < l; j++)
arr[i][j] = nu;
for (int i = 0; i < l; i++)
cin >> str[i];
cin >> t;
for (int i = 0; i < t; i++) {
string o, p;
int num;
cin >> o >> p >> num;
int oo = find(o), pp = find(p);
arr[oo][pp] = arr[pp][oo] = num;
e[i].begin = oo;
e[i].end = pp;
e[i].weight = num;
}
for (int i = 0; i < l; i++) {
for (int j = 0; j < l; j++)
cout << arr[i][j] << ' ';
cout << endl;
}
}
//克鲁斯卡尔算法
int find(int i) {
while (flag[i] > 0)
i = flag[i];
return i;
}
int find(const string &ss) {
for (int i = 0; i < l; i++)
if (str[i] == ss)
return i;
return -1;
}
//!!!!!!!克鲁斯卡尔算法!!!!!
void Kurskal() {
for (int i = 0; i < l; i++)
flag[i] = 0;
cout << "kruskal:" << endl;
//将所获得边集数组进行排序
for (int i = 0; i < t; i++)
for (int j = 0; j < t - i - 1; j++) {
if (e[j].weight > e[j + 1].weight)
swap(e[j], e[j + 1]);
}
for (int i = 0; i < l; i++) {
int o = find(e[i].begin);
int p = find(e[i].end);
if (o != p) {
flag[o] = p;
cout << str[e[i].begin] << ' ' << str[e[i].end] << ' ' << e[i].weight << endl;
}
}
}
//!!!!!!!!普里姆算法!!!!!!!!!
void Prim() {
Edge *q = new Edge[l];
string s;
cin >> s;
int start = find(s);
for (int i = 0; i < l; i++) {
arr[i][start] = 0;
}
int k = 0;
int next;
int remain = l - 1;
while (remain > 0) {
arr[start][l] = 1;
int min = 0xffff;
for (int i = 0; i < l; i++) {
if (arr[i][l] == 1) {
for (int j = 0; j < l; j++) {
if (arr[i][j] < min && arr[i][j] != 0) {
min = arr[i][j];
start = i;
next = j;
}
}
}
}
q[k].begin = str[start];
q[k].end = str[next];
q[k].weight = arr[start][next];
sum += arr[start][next];
k++;
for (int i = 0; i < l; i++) {
arr[i][next] = 0;
}
remain--;
start = next;
}
cout << sum << endl;
cout << "prim:" << endl;
for (int i = 0; i < k; i++)
cout << q[i].begin << ' ' << q[i].end << ' ' << q[i].weight << endl;
}
};