10、数据结构与算法—

一、什么是堆

堆是一种特殊的树形数据结构，通常实现为完全二叉树或满二叉树。堆又分为两种类型最大堆（Max Heap） 和 最小堆（Min Heap）

1.1、什么是二叉树

二叉树是一种数据结构，它是由n（n≥0）个节点的有限集合构成，每个节点最多有两个子节点，通常分别称为左子节点和右子节点。

n：表示二叉树中的节点总数，它可以是一个任意非负整数。
n≥0：这意味着二叉树可以包含任意数量的节点，包括零个。即：
当n=0时，表示这是一棵空二叉树，它不包含任何节点。
当n>0时，表示二叉树至少包含一个节点，并且根据定义，这个节点可能还有0个、1个或2个子节点，依此类推，形成一个节点的有限集合。
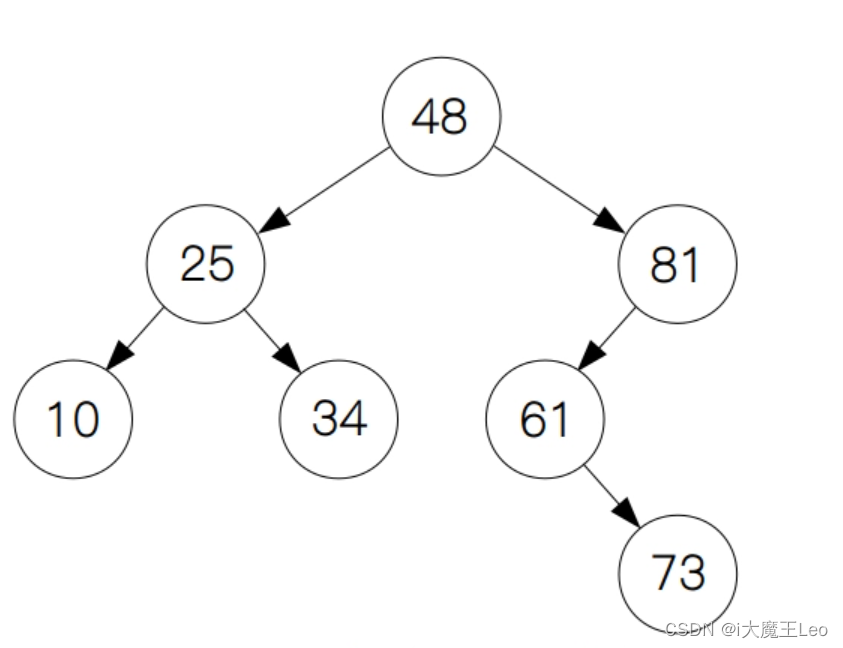
二叉树如下图：每个节点最多有两个子节点，通常分别称为左子节点和右子节点。

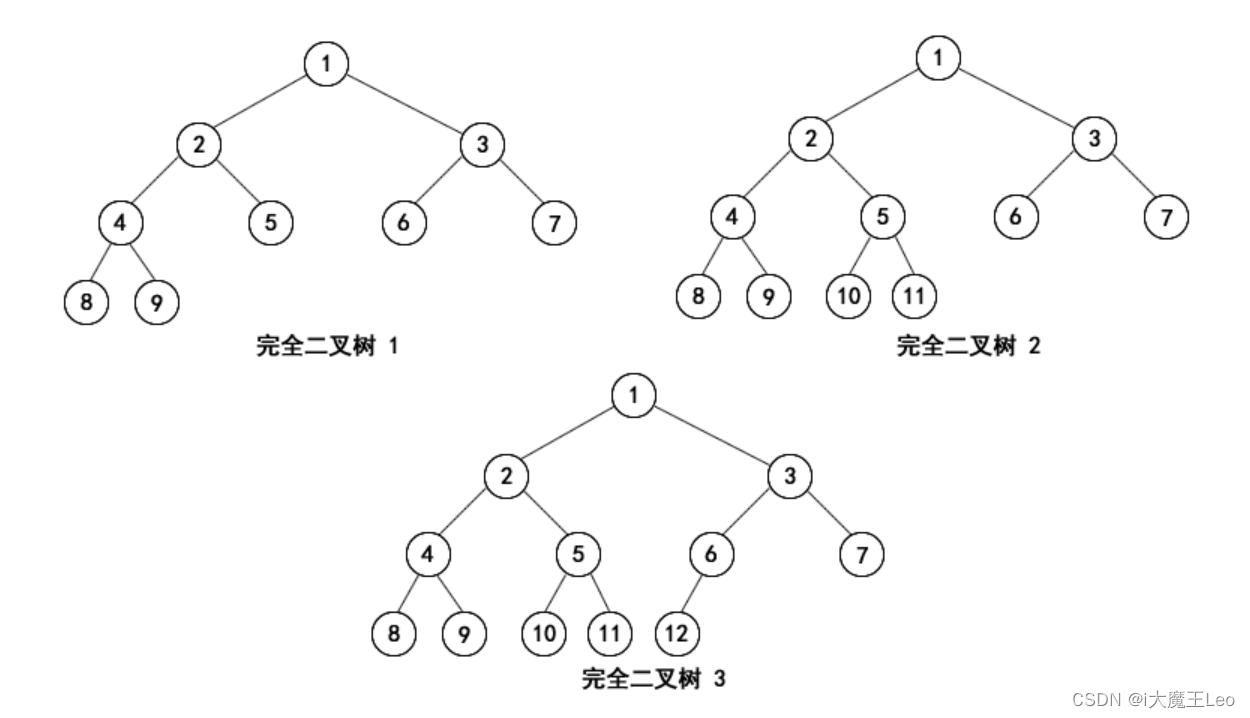
1.2、什么是完全二叉树

除了最后一层外，其他层都是完全填满的，最后一层的节点都尽可能地靠左排列，允许右侧存在空节点，但左侧不允许出现空位（除非右边的所有位置也都为空）。
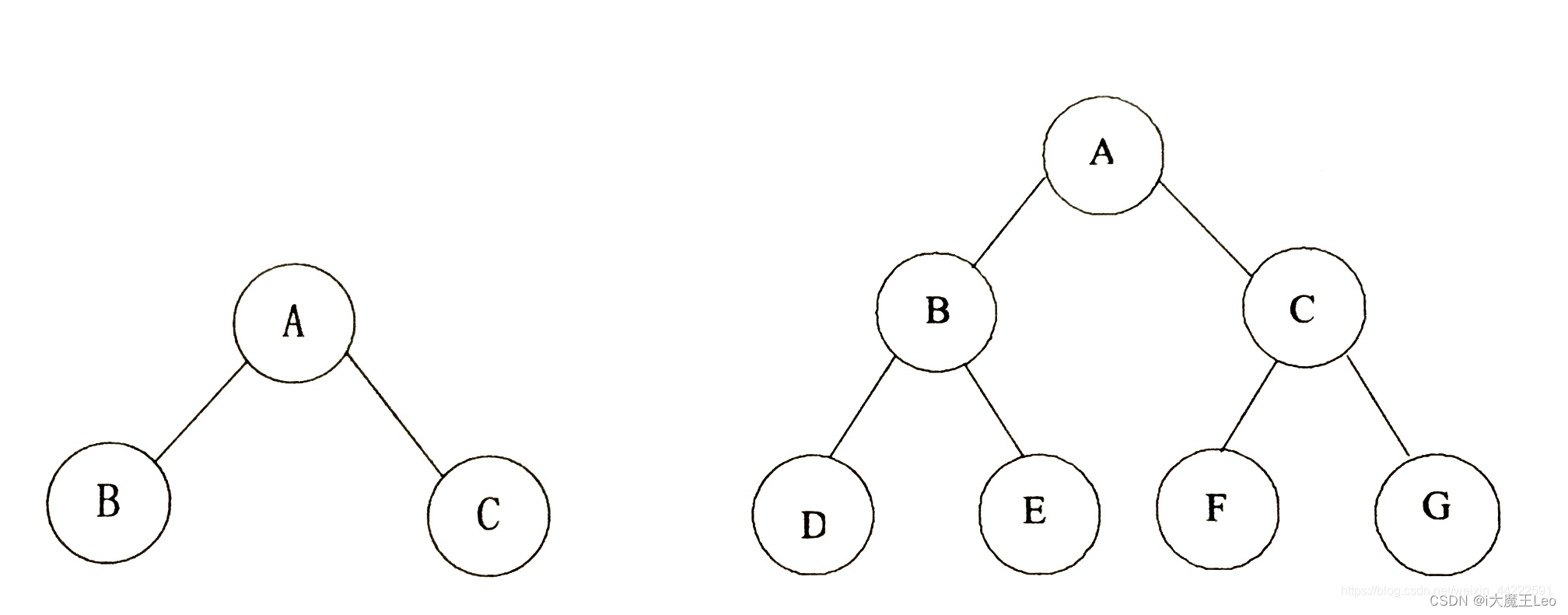
在这里插入图片描述

1.3、什么是满二叉树

所有层都被完全填满，且所有叶子节点都在最底层，没有空缺的位置。
在这里插入图片描述

1.4、什么是最大堆（或大顶堆）

对于任意节点，其父节点的值大于等于（≥）它的两个子节点的值。换句话说，堆顶元素（根节点）始终是整个堆中最大的元素。
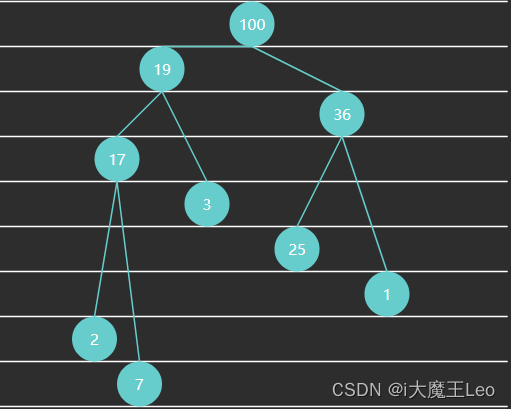
在这里插入图片描述

1.5、什么是最小堆（或小顶堆）

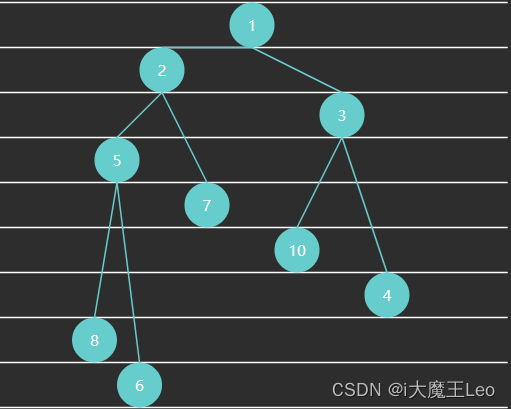
对于任意节点i，其父节点的值小于等于（≤）它的两个子节点的值。因此，在最小堆中，堆顶元素始终是最小的。
在这里插入图片描述

二、堆的应用场景

2.1、优先队列（Priority Queue）

堆可以高效地实现优先队列，其中元素按照它们的优先级（或值）进行排序。在最大堆中，优先级最高的元素位于根节点，每次删除时总是取出优先级最高的元素；在最小堆中，则是取出优先级最低的元素。

2.2、堆排序（Heapsort）

堆排序是一种基于比较的排序算法，它首先将待排序的序列构造成一个大顶堆或小顶堆，然后不断交换堆顶元素与末尾元素并调整堆结构，直到整个序列有序。

2.3、内存管理（Memory Management）

在操作系统中，内存分配器可能会使用堆数据结构来管理内存碎片和动态分配内存请求。尽管这里的“堆”通常指的是内存区域而不是数据结构，但在某些情况下，其分配策略会借鉴堆数据结构的特性。

2.4、图算法

Dijkstra算法、Prim算法和Kruskal算法等解决最短路径问题时，利用优先队列（通过堆实现）快速访问当前已知的最小距离节点。

2.5、事件调度

在实时系统和事件驱动的应用程序中，堆用于存储具有优先级的任务或事件，确保高优先级任务优先得到处理。

2.6、Top K问题

找出一组数据中的前K个最大或最小元素，可以通过维护大小为K的最小堆或最大堆快速得到结果。

2.7、总结

总之，堆提供了一种高效的数据结构来支持对大量数据进行快速查找、插入和删除操作，尤其当需要保持数据的某种顺序性或优先级时。

三、堆的特征

3.1、堆数据的存储方式可以用数组来实现。

如下图
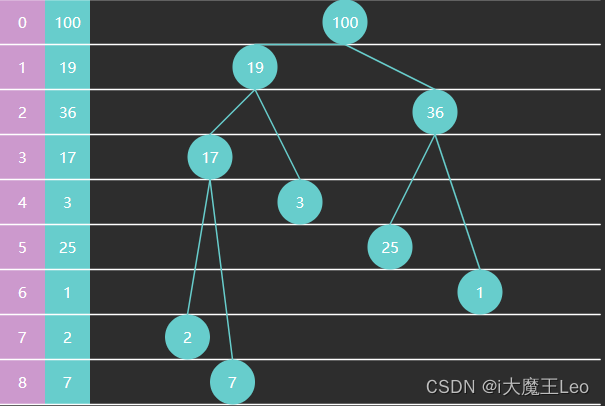
在这里插入图片描述

3.2、堆中父子节点的关系

3.2.1、如何获任意节点 i 的两个子节点索引位置

a、获取左边子元素

公式：

左子节点索引= (2 * i 的索引位置) + 1

案例：

如上图：17的索引位置是3 ,17的左子节点索引位置是7
7 = (3 * 2) + 1

b、获取右边子元素

公式：

右子节点索引= (2 * i 的索引位置) + 2

案例：

如上图：17的索引位置是3 ,17的右子节点索引位置是8
8 = (3 * 2) + 2

3.2.2、如何获任意节点 j 的父节点索引位置

公式：

父节点索引 =（ j的索引位置 - 1）/ 2 (除数向下取整)

案例：

案例1：如上图，17的索引位置是3 ,17的父节点索引位置是1
1 = ( 3 - 1 ) / 2

案例2：如上图，1的索引位置是6 ,1的父节点索引位置是2
1= ( 6 - 1 ) / 2 // 除数向下取整.

3.2.3、如何获堆中最后一个非叶子节点索引

公式：

最后一个非叶子节点的索引 = (堆中元素个数/2）-1 //除数向下取整

案例：

如上图；堆中元素共9个。
3 = ( 9 / 2) - 1 // 除数向下取整，索引位置3就是就是最后一个非叶子节点-》17

3.3、堆的常用方法（以大顶堆为例）

3.3.1、堆的初始化

为堆分配一个数组，并设定初始容量。

/**
 * 大顶堆
 */
public class MaxHeap {

    /**
     * 用数组存储堆元素
     */
    private int[] array;

    /**
     * 堆中元素个数
     */
    private int size;

    /**
     * @param capacity 堆的容量
     */
    public MaxHeap(int capacity) {
        this.array = new int[capacity];
        this.size = 0;
    }
}

3.3.2、建立堆

3.3.2.1、建立堆思路

传入一组随意的数组数据，然后从最后一个非叶子节点开始，依次往上对每个节点执行元素下潜操作，最终得到一个合法的堆结构。

3.3.2.2、具体代码

package heap;

/**
 * 大顶堆
 */
public class MaxHeap {

    /**
     * 用数组存储堆元素
     */
    private int[] array;

    /**
     * 堆中元素个数
     */
    private int size;

    /**
     * @param capacity 堆的容量
     */
    public MaxHeap(int capacity) {
        this.array = new int[capacity];
        this.size = 0;
    }

    /**
     * 建立堆思路：对于一组无序的数据，可以先将其放入一个数组中，然后从最后一个非叶子节点开始，
     * 依次往上对每个节点执行元素下潜操作，最终得到一个合法的堆结构。
     * <p>
     * 步骤：
     * 1、传入一个无序的数组数据。
     * 2、如何找到最后一个非叶子节点：公式为：（size/2）-1 就是最后一个非叶子节点索引位置。
     * 3、然后依次往上，对每个节点执行下潜。
     *
     * @param array 需要创建成堆的数组
     */
    public MaxHeap(int[] array) {
        this.array = array;
        this.size = array.length;
        //找到第一个叶子节点
        for (int i = (size / 2) - 1; i >= 0; i--) {
            down(i);
        }
    }

    /**
     * 元素下潜方法
     * 下潜原理：与左右两个子元素进行比较，如果最大的那个子元素大于当前下潜元素。
     * 那么与该子元素进行索引替换。注意事项：左右子元素的索引不能超过数组长度的范围(必须小于size)
     *
     * @param diveIndex 下潜元素索引
     */
    private void down(int diveIndex) {
        int leftIndex = (diveIndex * 2) + 1;  //获取左边子元素索引
        int rightIndex = leftIndex + 1;//获取右边子元素索引；等同于(diveIndex * 2) + 2
        int max = diveIndex;  //第一个临时变量记录最大那个子元素索引。默认为-1；

        //如果左边子元素大于下潜元素，max记录左边子元素索引
        if (leftIndex < size && array[leftIndex] > array[max]) {
            max = leftIndex;
        }
        //如果右边子元素大于下潜元素，max记录右边子元素索引
        if (rightIndex < size && array[rightIndex] > array[max]) {
            max = rightIndex;
        }

        //不等于-1 表示有比下潜元素大的子元素
        if (max != diveIndex) {
            //交换元素位置
            swap(diveIndex, max);
            down(max);//然后继续下潜
        }
    }

    /**
     * 元素索引交换方法。
     */
    private void swap(int i, int j) {
        int t = array[i];
        array[i] = array[j];
        array[j] = t;
    }
}

3.3.2.3、测试

代码

    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5, 6, 7};
        MaxHeap maxHeap=new MaxHeap(array);
        System.out.println(Arrays.toString(maxHeap.array));
    }

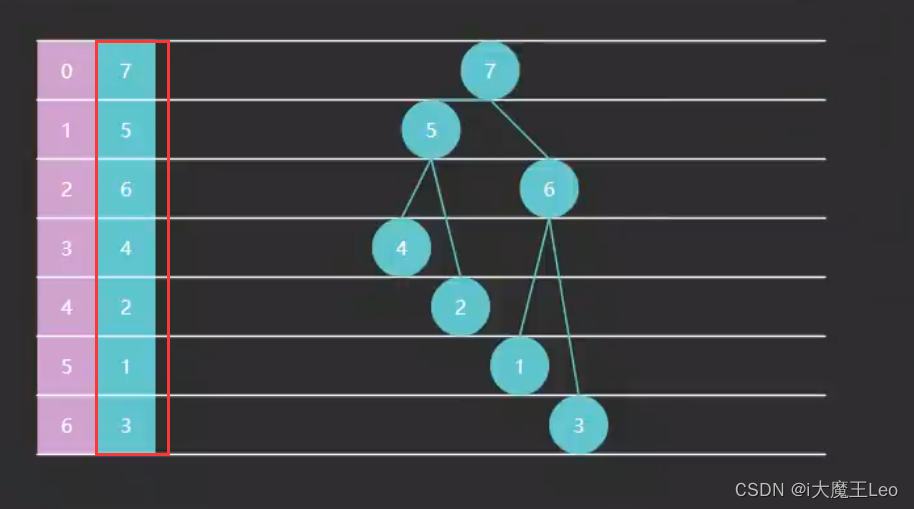
测试前的堆
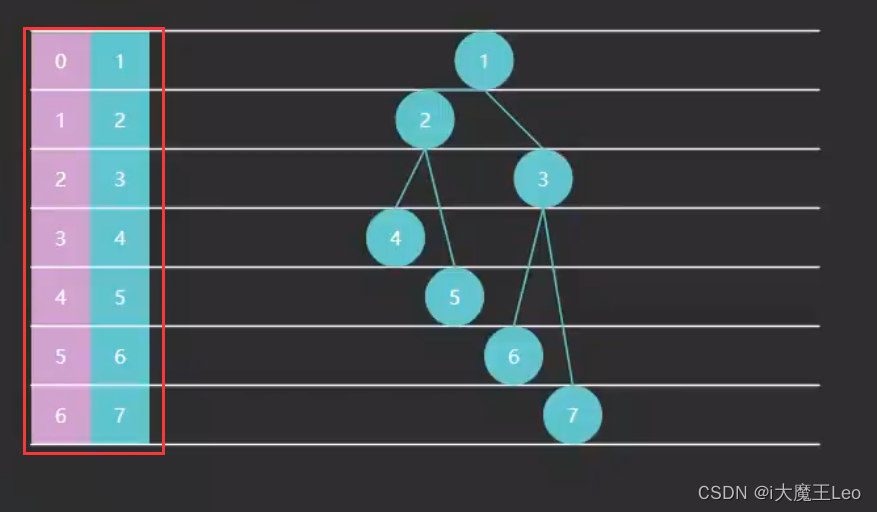
在这里插入图片描述
输出结果

[7, 5, 6, 4, 2, 1, 3]

在这里插入图片描述

3.3.3、获取堆顶元素

3.3.3.1、实现思路

在大顶堆中，最大元素总是位于根节点。所以。首先移除根节点做一个临时存储，用于返回结果，然后将根节点元素与最后一个元素进行索引调整，这时根节点到了数组最后面。直接将最后一个值赋值为空，最后然后把新的根节点向下调整（称为“下潜”或“heapify-down”），使其满足堆性质。

3.3.3.2、代码

    /**
     * 获取堆顶元素
     *
     * @return
     */
    public int poll() {
        int data = array[0];//临时存储堆顶元素
        swap(0, size - 1);//将堆顶元素和最后一个元素跟换索引位置
        array[size - 1] = -1;//表示赋值为空（-1），
        size--;//元素个数-1；
        down(0);//然后把新的根节点向下调整（称为“下潜”或“heapify-down”），使其满足堆性质。
        return data;
    }

3.3.3.3、测试

    public static void main(String[] args) {
        int[] array = {1, 2, 3, 4, 5, 6, 7};

        MaxHeap maxHeap = new MaxHeap(array);
        int peek = maxHeap.poll();
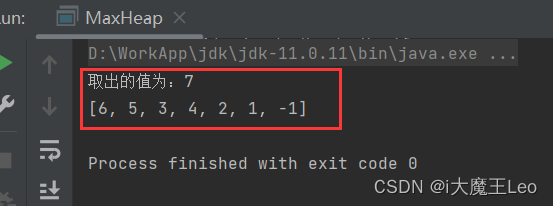
        System.out.println("取出的值为：" + peek);
        System.out.println(Arrays.toString(maxHeap.array));
    }

在这里插入图片描述

3.3.4、获取指定索引位置元素（和获取堆顶元素逻辑类似）

    /**
     * 获取指定索引元素
     *
     * @return
     */
    public int poll(int index) {
        int data = array[index];//临时存储堆顶元素
        swap(index, size - 1);//将堆顶元素和最后一个元素跟换索引位置
        array[size - 1] = -1;//表示赋值为空（-1），
        size--;//元素个数-1；
        down(index);//然后把新的index节点向下调整（称为“下潜”或“heapify-down”），使其满足堆性质。
        return data;
    }

3.3.5、替换堆顶元素

    /**
     * 替换堆顶元素
     *
     * @param replaced 新元素
     */
    public void replace(int replaced) {
        array[0] = replaced;
        down(0); // 然后把新的根节点向下调整（称为“下潜”或“heapify-down”），使其满足堆性质。
    }

3.3.6、堆添加元素

3.3.6.1、实现思路

当向堆中插入一个新元素时，通常会将新元素添加到堆的末尾（数组的下一个空闲位置），然后通过自下而上的调整过程（称为“上浮”或“heapify-up”）来确保新的堆仍满足堆性质。

3.3.6.2、代码

    /**
     * 堆的尾部添加元素
     *
     * @param offered 新元素
     * @return 是否添加成功
     */
    public boolean offer(int offered) {
        //数组是否已满。
        if (size == array.length) {
            return false;
        }
        up(offered);//元素上浮
        size++;//元素个数+1
        return true;
    }

    // 将 offered 元素上浮: 直至 offered 小于父元素或到堆顶
    private void up(int offered) {
        int child = size;//需要上浮的所以位置
        while (child > 0) {//如果上浮位置大于0表示还可以上浮
            int parent = (child - 1) / 2;//获取上浮索引的父索引位置

            //如果新元素大于父元素，将元素赋值到新元素位置
            if (offered > array[parent]) {
                array[child] = array[parent];
            } else {
                break;
            }
            child = parent;//将父元素索引设置为需要上符的索引
        }
        array[child] = offered;//上浮结束。那么将最终的上浮位置设置为新元素。
    }