MATLAB中的hilb函数用于生成希尔伯特矩阵。

语法为:

H = hilb(n)

其中:

n: 生成的希尔伯特矩阵的阶数

H: 生成的n阶希尔伯特矩阵

希尔伯特矩阵又称为希尔伯特运算矩阵,它是一种测试矩阵,元素H(i,j) = 1/(i+j-1),i和j表示矩阵的行号和列号。

例如:

H = hilb(7)会生成一个7阶的希尔伯特矩阵:

>> H = hilb(7)

H =

    1.0000    0.5000    0.3333    0.2500    0.2000    0.1667    0.1429
    0.5000    0.3333    0.2500    0.2000    0.1667    0.1429    0.1250
    0.3333    0.2500    0.2000    0.1667    0.1429    0.1250    0.1111
    0.2500    0.2000    0.1667    0.1429    0.1250    0.1111    0.1000
    0.2000    0.1667    0.1429    0.1250    0.1111    0.1000    0.0909
    0.1667    0.1429    0.1250    0.1111    0.1000    0.0909    0.0833
    0.1429    0.1250    0.1111    0.1000    0.0909    0.0833    0.0769

hilb函数主要用来测试矩阵运算和逆矩阵计算的程序。

hilb函数生成的希尔伯特矩阵主要有以下几个用途:

1. 测试矩阵运算程序

希尔伯特矩阵每一个元素都有精确的表示,可以用来测试矩阵乘法、逆矩阵计算等矩阵运算程序的正确性。

1. 分析矩阵数值算法的稳定性

希尔伯特矩阵的条件数随矩阵阶数增长而快速恶化,可以用来测试不同的矩阵算法在条件数差的矩阵上是否数值稳定。

1. 矩阵函数的插值运算

希尔伯特矩阵满足一定的互反性,可以用于矩阵函数值的插值运算。

1. 理论物理学研究

在量子力学和量子场论中,希尔伯特矩阵都有应用,可以用于描述理论模型。

1. 测试编程语言矩阵运算能力

希尔伯特矩阵可以很快构造,但矩阵运算复杂,可以用来测试各种编程语言的矩阵运算速度和准确性。

总的来说,hilb函数生成的希尔伯特矩阵可以作为矩阵算法和程序的测试用例,也可以为理论物理研究提供帮助。这是它的主要用途。

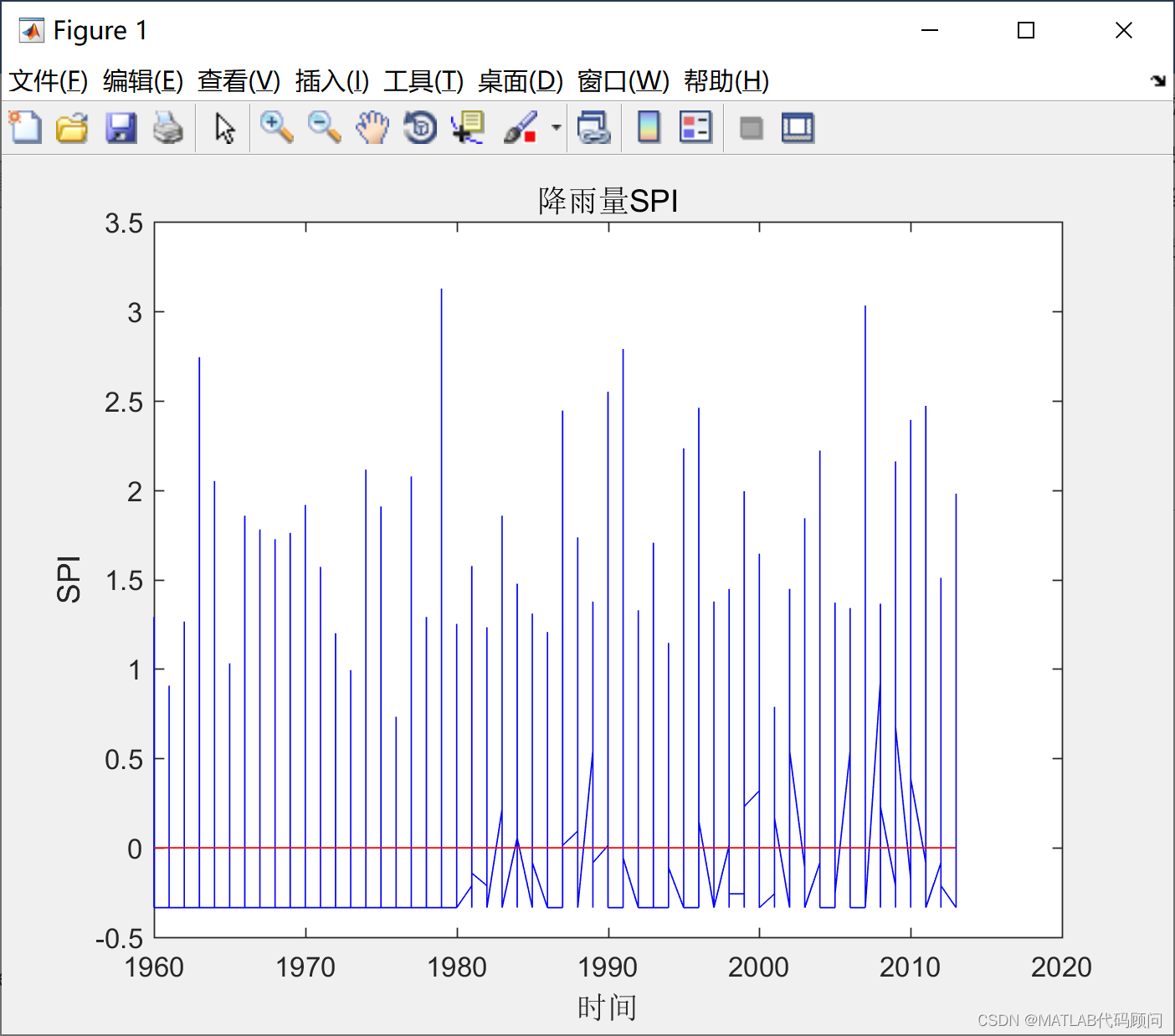
可视化结果如下:

>> H = hilb(256)*256/4;
>> imshow(H)