基于仿射区间的分布式三相不对称配电网潮流算法matlab仿真

news2024/9/21 10:53:39

目录

1.课题概述

2.系统仿真结果

3.核心程序与模型

4.系统原理简介

5.完整工程文件

1.课题概述

       基于仿射区间的分布式三相不对称配电网潮流算法matlab仿真。 基于仿射区间的，含分布式电源的配电网三相潮流算法，算法涉及仿射，三相，分布式电源注入等。

2.系统仿真结果

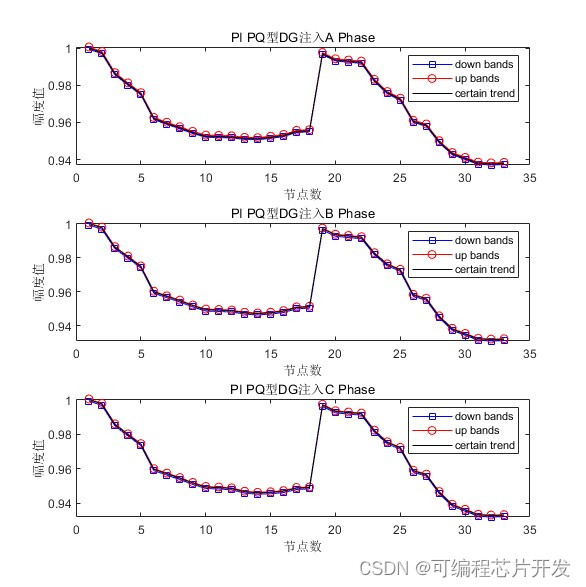
3.核心程序与模型

版本：MATLAB2022a

................................................................................

%%
%开始迭代
S0     = S;
k      = 0;
Us     = zeros(N,3,2*N+1+2*(Max_Iteration-1)*N);
TempUs = Us;
active = 2*N+1; 
UsA    = zeros(N,2*N+1+2*(Max_Iteration-1)*N);
TempUsA= UsA; 

UsB    = zeros(N,2*N+1+2*(Max_Iteration-1)*N);
TempUsB= UsB; 

UsC    = zeros(N,2*N+1+2*(Max_Iteration-1)*N);
TempUsC= UsC; 


while k < Max_Iteration
    
      k = k + 1;
      
      %计算PI节点的Qk 
      if nPI > 0
         QPI          = [sqrt((DG(PINum,18)./I_base).^2.*abs(U(PIbus,2)).^2 - (DG(PINum,4)/P_base).^2),...
                         sqrt((DG(PINum,19)./I_base).^2.*abs(U(PIbus,3)).^2 - (DG(PINum,6)/P_base).^2),...
                         sqrt((DG(PINum,20)./I_base).^2.*abs(U(PIbus,4)).^2 - (DG(PINum,8)/P_base).^2)]; 
         S(PIbus,2:4) =  S0(PIbus,2:4) + QPI;    
      end
..................................................................
      
      %考虑DG节点
      if nPV > 0
         UPVbus   = U(PVbus,:);    
         DeltaUDG = [PVbus,real(UDG(:,2)-UPVbus(:,2)),real((UDG(:,3)-UPVbus(:,3))*exp(1i*2/3*pi)),real((UDG(:,4)-UPVbus(:,4))*exp(-1i*2/3*pi))];        
         DeltaQ   = ZXinv*reshape(DeltaUDG(:,2:4)',size(Q,1)*size(Q,2),1);
         %更新PV型DG的Q值
         Q        = Q + DeltaQ;     
         QMatr    = reshape(Q,3,size(Q,1)*size(Q,2)/3)';    
         %检查 PV 节点的无功越界情况
         for m = 1:nPV
             for j = 1:3
                 if(QMatr(m,j) > DG(PVNum(m),10))
                    QMatr(m,j) = DG(PVNum(m),10);
                 elseif (QMatr(m,j) < DG(PVNum(m),11))
                    QMatr(m,j) = DG(PVNum(m),11);
                 end
             end
         end
         Q = reshape(QMatr',size(Q,1)*size(Q,2),1);
      end
end


A_infor(1,:)=  maxreal1A(:);
A_infor(2,:)= -minreal1A(:);
A_infor(3,:)=  maximag1A(:);
A_infor(4,:)= -minimag1A(:);
B_infor(1,:)= -maxreal1B(:);
B_infor(2,:)=  minreal1B(:);
B_infor(3,:)= -maximag1B(:);
B_infor(4,:)=  minimag1B(:);
C_infor(1,:)= -maxreal1C(:);
C_infor(2,:)=  minreal1C(:);
C_infor(3,:)=  maximag1C(:);
C_infor(4,:)= -minimag1C(:);
maxreal_phase1 = A_infor(1,:);
minreal_phase1 = A_infor(2,:); 
maximag_phase1 = A_infor(3,:); 
minimag_phase1 = A_infor(4,:); 
maxreal_phase2 = B_infor(1,:); 
minreal_phase2 = B_infor(2,:);  
maximag_phase2 = B_infor(3,:); 
minimag_phase2 = B_infor(4,:); 
maxreal_phase3 = C_infor(1,:); 
minreal_phase3 = C_infor(2,:); 
maximag_phase3 = C_infor(3,:); 
minimag_phase3 = C_infor(4,:); 
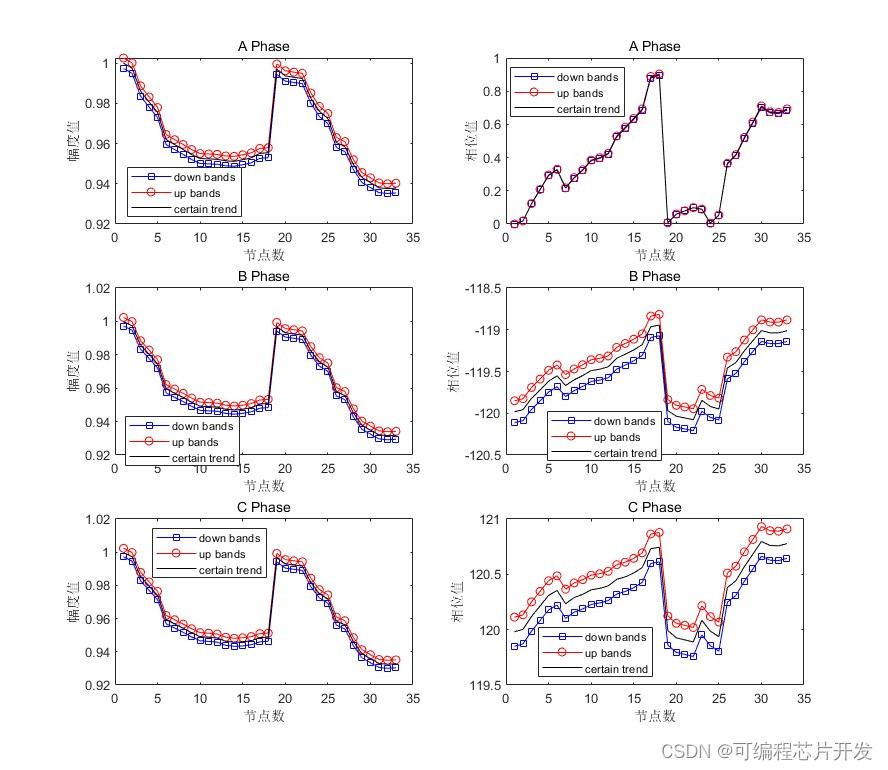
%得到三相仿射的区间值
[V_abs_phase1,V_ang_phase1]   = func_affine_result(maxreal_phase1,minreal_phase1,maximag_phase1,minimag_phase1,N);
[V_abs_phase2,V_ang_phase2]   = func_affine_result(maxreal_phase2,minreal_phase2,maximag_phase2,minimag_phase2,N);
[V_abs_phase3,V_ang_phase3]   = func_affine_result(maxreal_phase3,minreal_phase3,maximag_phase3,minimag_phase3,N);

figure;
subplot(321);
plot(V_abs_phase1(:,1),'b-s');
hold on;
plot(V_abs_phase1(:,2),'r-o');
hold on;
plot(mean(V_abs_phase1,2),'k');
hold off;
xlabel('节点数');
ylabel('幅度值');
title(['A Phase']);
legend('down bands','up bands','certain trend');
disp('A相幅度值');
V_abs_phase1


subplot(322);
plot(V_ang_phase1(:,1),'b-s');
hold on;
plot(V_ang_phase1(:,2),'r-o');
hold on;
plot(mean(V_ang_phase1,2),'k');
hold off;
xlabel('节点数');
ylabel('相位值');
title(['A Phase']);
legend('down bands','up bands','certain trend');
disp('A相相位值');
V_ang_phase1



subplot(323);
plot(V_abs_phase2(:,1),'b-s');
hold on;
plot(V_abs_phase2(:,2),'r-o');
hold on;
plot(mean(V_abs_phase2,2),'k');
hold off;
xlabel('节点数');
ylabel('幅度值');
title(['B Phase']);
legend('down bands','up bands','certain trend');
disp('B相幅度值');
V_abs_phase2

subplot(324);
plot(V_ang_phase2(:,1),'b-s');
hold on;
plot(V_ang_phase2(:,2),'r-o');
hold on;
plot(mean(V_ang_phase2,2),'k');
hold off;
xlabel('节点数');
ylabel('相位值');
title(['B Phase']);
legend('down bands','up bands','certain trend');
disp('B相相位值');
V_ang_phase2



subplot(325);
plot(V_abs_phase3(:,1),'b-s');
hold on;
plot(V_abs_phase3(:,2),'r-o');
hold on;
plot(mean(V_abs_phase3,2),'k');
hold off;
xlabel('节点数');
ylabel('幅度值');
title(['C Phase']);
legend('down bands','up bands','certain trend');
disp('C相幅度值');
V_abs_phase3


subplot(326);
plot(V_ang_phase3(:,1),'b-s');
hold on;
plot(V_ang_phase3(:,2),'r-o');
hold on;
plot(mean(V_ang_phase3,2),'k');
hold off;
xlabel('节点数');
ylabel('相位值');
title(['C Phase']);
legend('down bands','up bands','certain trend');
disp('C相相位值');
V_ang_phase3

fprintf('    节点      A幅值下限  A幅值上限 B幅值下限  B幅值上限 C幅值下限  C幅值上限  A幅角下限 A幅角上限 B幅角下限  B幅角上限 C幅角下限  C幅角上限');
RR = [[1:33]',V_abs_phase1,V_abs_phase2,V_abs_phase3,V_ang_phase1,V_ang_phase2,V_ang_phase3]


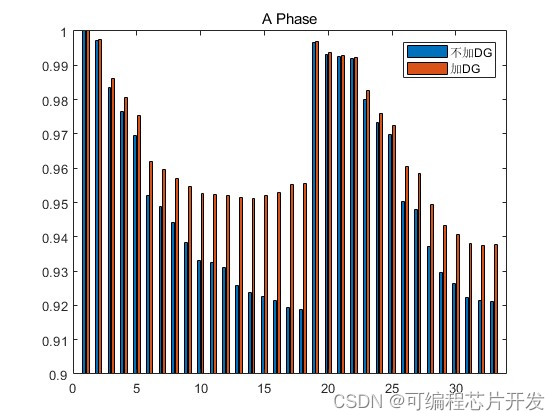
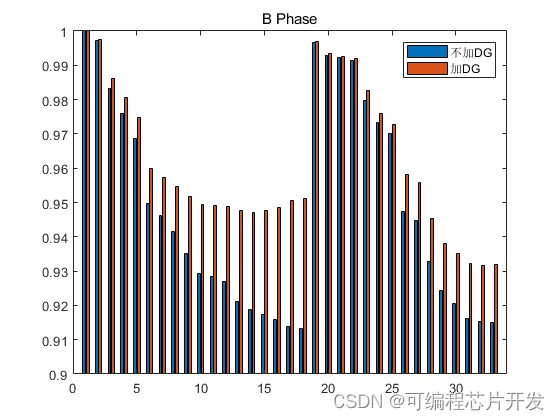
%是否加入分布式电源的对比
load func\No_DG.mat
figure;
r1 = [a,abs(U(:,2))];
bar(r1);
axis([0,34,0.9,1]);
legend('不加DG','加DG');
title('A Phase');

figure;
r2 = [b,abs(U(:,3))];
bar(r2);
axis([0,34,0.9,1]);
legend('不加DG','加DG');
title('B Phase');

figure;
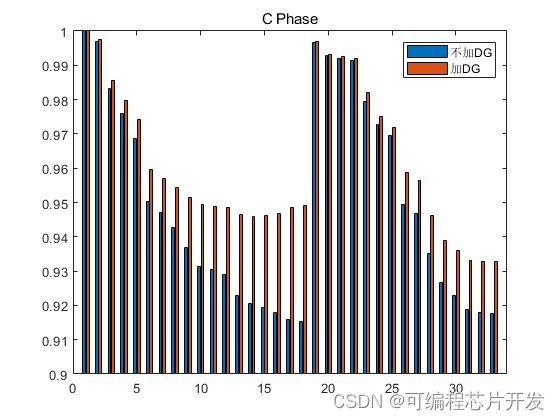
r3 = [c,abs(U(:,4))];
bar(r3);
axis([0,34,0.9,1]);
legend('不加DG','加DG');
title('C Phase');

fprintf('网损');
DeltaSL*1000*P_base
02_021m

4.系统原理简介

       当只采用区间运算，得到的结果则有可能过于保守，而采用仿射运算后，本文方法能够得到更窄的不确定区域，从而得到更窄的区间。从如下的三个方面角度考虑：

      理想状态下的，确定性潮流计算——即对应本课题的“含分布式电源的配电网三相潮流算法”。

       实际状态下，不确定性潮流计算，这里对应两个类型的算法：

a.基于区间算法的含分布式电源的配电网三相潮流算法，不过结果范围较大，过于保守。

b.基于仿射算法的含分布式电源的配电网三相潮流算法，其结果范围较小，效果较a更优。

         我们将主要针对b算法进行编程。

       传统的配电网中的节点类型一般是PQ节点，而加入分布式电源之后，会产生PV节点和PI节点，因此，在针对还有分布式电源的配电网进行潮流计算的时候，必须根据不同的节点类型采用不同的处理方法，但本质上就是在潮流计算的时候将各种类型的节点转换为潮流计算能够处理的PQ点或者PV点。

5.完整工程文件

v

v

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1424271.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

python爬虫概念及介绍

python爬虫概念及介绍

1. 什么是互联网爬虫&#xff1f; 解释 1 &#xff1a;通过一个程序&#xff0c;根据 Url ( http : // www . taobao . com ) 进行爬取网页&#xff0c;获取有用信息 解释 2&#xff1a;使用程序模拟浏览器&#xff0c;去向服务器发送请求&#xff0c;获取响应信息 2. 爬虫核…
阅读更多...
深度学习经典模型之BERT(下）

深度学习经典模型之BERT(下）

在"深度学习经典模型之BERT(上)"我们描述了BERT基本信息、意义、与GPT和Transformer的区别、预训练、自监督等相关信息后&#xff0c;本章节将介绍BERT的输入、Encoder、微调及两个主流变种。 BERT inputs 切词方法 BERT的切词方法用的是WordPiece embeddings&…
阅读更多...
MongoDB数据模型和WiredTiger读写模型

MongoDB数据模型和WiredTiger读写模型

MongoDB数据模型 思考&#xff1a;MongoDB为什么会使用BSON&#xff1f; BSON协议与数据类型 JSON JSON是当今非常通用的一种跨语言Web数据交互格式&#xff0c;属于ECMAScript标准规范的一个子集。JSON&#xff08;JavaScript Object Notation, JS对象简谱&#xff09;即J…
阅读更多...
[word] word艺术字体如何设置？ #知识分享#职场发展#媒体

[word] word艺术字体如何设置？ #知识分享#职场发展#媒体

word艺术字体如何设置&#xff1f; 在工作中有些技巧&#xff0c;可以快速提高工作效率&#xff0c;解决大部分工作&#xff0c;今天给大家分享word艺术字体如何设置的技巧&#xff0c;希望可以帮助到你。 1、设置艺术字 选中文字&#xff0c;然后点击菜单栏的【插入】按钮一一…
阅读更多...
机器学习复习（6）——numpy的数学操作

机器学习复习（6）——numpy的数学操作

加减法运算 # 创建两个不同的数组 a np.arange(4) #list(0,1,2,3 b np.array([5,10,15,20]) # 两个数组做减法运算 b-a 运行结果&#xff1a; 计算数组的平方 #b*2代表数组b每个元素乘以2 #b**2代表数组b每个元素的2次方 b**2 运行结果&#xff1a; 计算数组的正弦值 #…
阅读更多...
8.DNS域名解析服务器

8.DNS域名解析服务器

目录 1. 概述 1.1. 产生原因 1.2. 作用&#xff1a; 1.3. 连接方式 1.4. 因特网的域名结构 1.4.1. 拓扑&#xff1a; 1.4.2. 分类 1.4.3. 域名服务器类型划分 2. DNS域名解析过程 2.1. 分类&#xff1a; 2.2. 解析图&#xff1a; 2.2.1. 图&#xff1a; 2.2.2. 过…
阅读更多...
【学网络安全】kali linux入门及常用简单工具介绍（附工具包）

【学网络安全】kali linux入门及常用简单工具介绍（附工具包）

前言 相信很多同学了解到和学习网络安全的时候都听过kali系统&#xff0c;大家都称之为黑客最喜爱的系统&#xff0c;那么什么是kali&#xff0c;初学者用kali能做些什么&#xff0c;我将在本文中做简单的介绍 一、kali linux是什么&#xff1f; Kali Linux 是专门用于渗透测…
阅读更多...
数据结构_单链表题-2.1

数据结构_单链表题-2.1

一. 反转单链表 将一个单链表反过来。 个人思路&#xff08;一团浆糊大错特错&#xff09; 反转嘛&#xff0c;变最后为起点&#xff0c;依次反转过来就行了。 1&#xff09;找到最后三个链表结点&#xff0c;分别保存下来&#xff0c;以最后一个为首地址。 2&#xff09;最…
阅读更多...
整数对最小和 - 华为OD统一考试

整数对最小和 - 华为OD统一考试

OD统一考试&#xff08;C卷&#xff09; 分值&#xff1a; 100分 题解&#xff1a; Java / Python / C 题目描述 给定两个整数数组array1、array2&#xff0c;数组元素按升序排列。 假设从array1、array2中分别取出一个元素可构成一对元素&#xff0c;现在需要取出k对元素&am…
阅读更多...
Qt扩展-muParser数学公式解析

Qt扩展-muParser数学公式解析

muParser数学公式解析 一、概述1. 针对速度进行了优化2. 支持的运算符3. 支持的函数4. 用户定义的常量5. 用户定义的变量6. 自定义值识别回调7. 其他功能 二、内置函数三、内置二元运算符四、三元运算符五、内置常量六、源码引入1. 源码文件2. 编译器开关1. MUP_BASETYPE2.MUP_…
阅读更多...
配置支持 OpenAPI 的 ASP.NET Core 应用

配置支持 OpenAPI 的 ASP.NET Core 应用

写在前面 Swagger 是一个规范和完整的框架&#xff0c;用于生成、描述、调用和可视化 RESTful 风格的 Web 服务。 本文记录如何配置基于Swagger 的 ASP.NET Core 应用程序的 OpenAPI 规范。 需要从NuGet 安装 Swashbuckle.AspNetCore 包 代码实现 var builder WebApplicati…
阅读更多...
如何在 Golang 中使用 crypto/ed25519 进行数字签名和验证

如何在 Golang 中使用 crypto/ed25519 进行数字签名和验证

如何在 Golang 中使用 crypto/ed25519 进行数字签名和验证 引言crypto/ed25519 算法简介环境搭建和准备工作生成密钥对进行数字签名 验证签名实际应用场景案例总结 引言 在当今数字化时代&#xff0c;网络安全显得尤为重要。无论是在网上进行交易、签署合同&#xff0c;还是发…
阅读更多...
大模型创业的3条军规

大模型创业的3条军规

上周&#xff0c;一家初创公司未能围绕LLM和 RAG 开展业务&#xff0c;尽管他们获得了第一份 B2B 大型合同。 以下是原因以及如何避免这种情况&#xff1a; 创始人写了一篇博客解释了为什么他不得不关闭他的业务&#xff0c;我在这里总结了他的要点。 NSDT工具推荐&#xff1a…
阅读更多...
基于VMware和Unbuntu18.04编译 嘉立创·泰山派 Linux SDK

基于VMware和Unbuntu18.04编译 嘉立创·泰山派 Linux SDK

主机硬件要求 内存最少32G 硬盘腾出200-500G&#xff0c;虽然编译最终占了73G&#xff0c;但富余一些以后可以搞别的方便 操作系统win7/10/11 VMware 安装 1.去vmware官网下载&#xff1a;https://customerconnect.vmware.com/cn/downloads/info/slug/desktop_end_user_comp…
阅读更多...
docker安装elasticsearch+kibana

docker安装elasticsearch+kibana

目录 1.安装es 2.安装kibana 3.kibana监控es 1.安装es 拉取镜像 docker pull elasticsearch:7.6.1 创建存放配置文件、数据、插件的各个文件夹 mkdir -p /home/docker/elasticsearch/config mkdir -p /home/docker/elasticsearch/data mkdir -p /home/docker/elasticsearch…
阅读更多...
2024最新版MongoDB安装使用指南

2024最新版MongoDB安装使用指南

2024最新版MongoDB安装使用指南 Installation and Usage Guide of the Latest MongoDB Community Edition in 2024 By JacksonML MongoDB is a document database with the scalability and flexibility that you want with the querying and indexing that you need. – mon…
阅读更多...
网络异常案例三_RST

网络异常案例三_RST

问题现象 在做功能测试的时候&#xff0c;经常看到设备离线的消息&#xff08;MQTT遗嘱&#xff09;。 在终端连接的网络设备上抓包分析&#xff0c;看到终端设备发起大量的RST请求。 151这个设备&#xff0c;7min&#xff0c;重置断开了8个TCP连接&#xff08;mqtt连接&#…
阅读更多...
Ansible自动化运维实战

Ansible自动化运维实战

一、abstract简介 ansible是新出现的自动化运维工具&#xff0c;基于Python开发&#xff0c;集合了众多运维工具(puppet、cfengine、chef、func、fabric) 的优点&#xff0c;实现了批量系统配置、批量程序部署、批量运行命令等功能.无客户端。我们要学一些Ansible的安装和一些基…
阅读更多...
地平线旭日 X3 VNC 远程桌面灰屏解决

地平线旭日 X3 VNC 远程桌面灰屏解决

解决 windows 使用 VNC 远程连接地平线旭日 X3 开发板桌面环境灰屏的问题。 1 查看问题 通过启动vncserver后的log文件确认问题。 启动 vnc 服务 vncserver :1通过 terminal 输出可以看到日志文件的存储位置 打开查看该文件后发现首当其冲是权限问题&#xff1a;说xstartup…
阅读更多...
【spring】springcloud中的组件有那些？

【spring】springcloud中的组件有那些？

&#x1f34e;个人博客&#xff1a;个人主页 &#x1f3c6;个人专栏&#xff1a;spring ⛳️ 功不唐捐&#xff0c;玉汝于成 目录 正文 我的其他博客 正文 说出主要的组件&#xff1a; Spring Cloud Eureka,服务注册中心,特性有失效剔除、服务保护Spring Cloud Zuul,API服…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023