前言

开始之前先简单扯几句，算法一直是我觉得很难也不太愿意主动去接触的，《算法（第四版）》这本书我大概几年前就知道了，一翻开就跟天书一样（当然现在也没好到哪里去），不过就是得要逼着自己不断学习嘛。

想要强调的是，学习笔记是比较个人以及主观的学习总结，没有任何的盈利目的，只是为了自我学习的提高，所以在文章里面我都会贴出来我所找到以及用到的资料，没有的或者是拓展性的内容请自行搜索。
（我非常需要在这里吐槽一下：偶尔有评论问我要源码……开源项目就不能动动手搜索一下？？？）

再次声明，学习笔记的受众首先是我本人，并不是为了教会各位成为大神，所以建议各位自己去看相关资料，自行总结，代码多敲多 debug 几遍，资料多看几遍，也许您的收获会比我多得多。

参考目录

• B站 普林斯顿大学《Algorithms》视频课
  （请自行搜索。主要以该视频课顺序来进行笔记整理，课程讲述的教授本人是该书原版作者之一 Robert Sedgewick。）
• 微信读书《算法（第4版）》
  （本文主要内容来自《1.5 案例研究：union-find算法》）
• 官方网站
  （有书本配套的内容以及代码）

学习笔记

注1：下面引用内容如无注明出处，均是书中摘录。
注2：所有 demo 演示均为视频 PPT demo 截图。

(截图自视频 PPT)

开发一个有用算法的步骤：

• 建立问题模型。
• 找到一个解决算法。
• 这个算法是否够快？存储空间是否足够？
• 如果上面的问题是否，搞清楚原因。
• 找到这些问题的根源。
• 提出新的算法，循环直到满意为止。

本章节主要是对 union-find 算法的实现以及分析。

1：动态连通性

动态连通性的特性说明：

我们假设“相连”是一种等价关系，这也就意味着它具有：

• 自反性：p和p是相连的；
• 对称性：如果p和q是相连的，那么q和p也是相连的；
• 传递性：如果p和q是相连的且q和r是相连的，那么p和r也是相连的。

方法 API：

edu.princeton.cs.algs4.UF

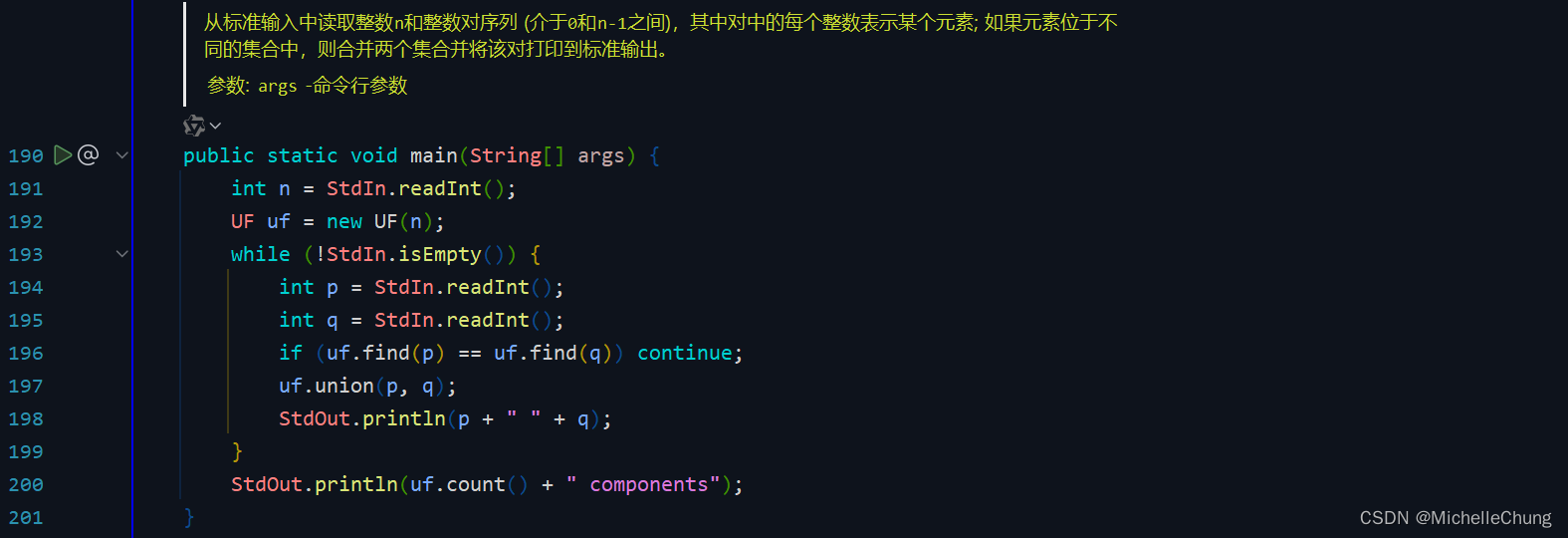
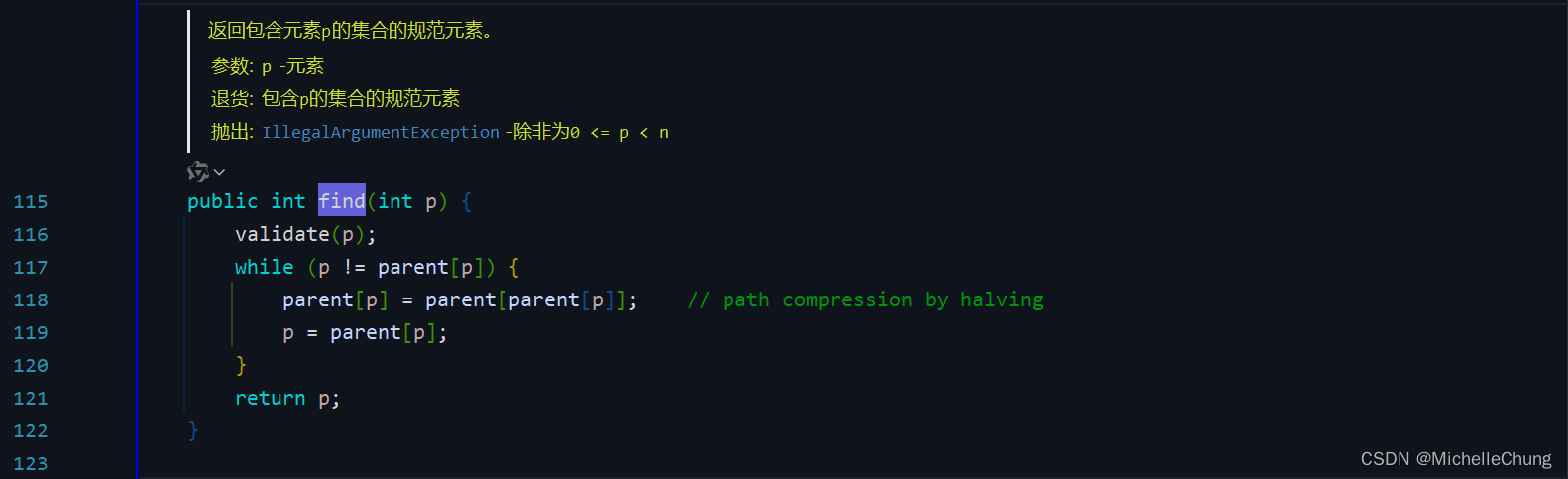
edu.princeton.cs.algs4.UF#find

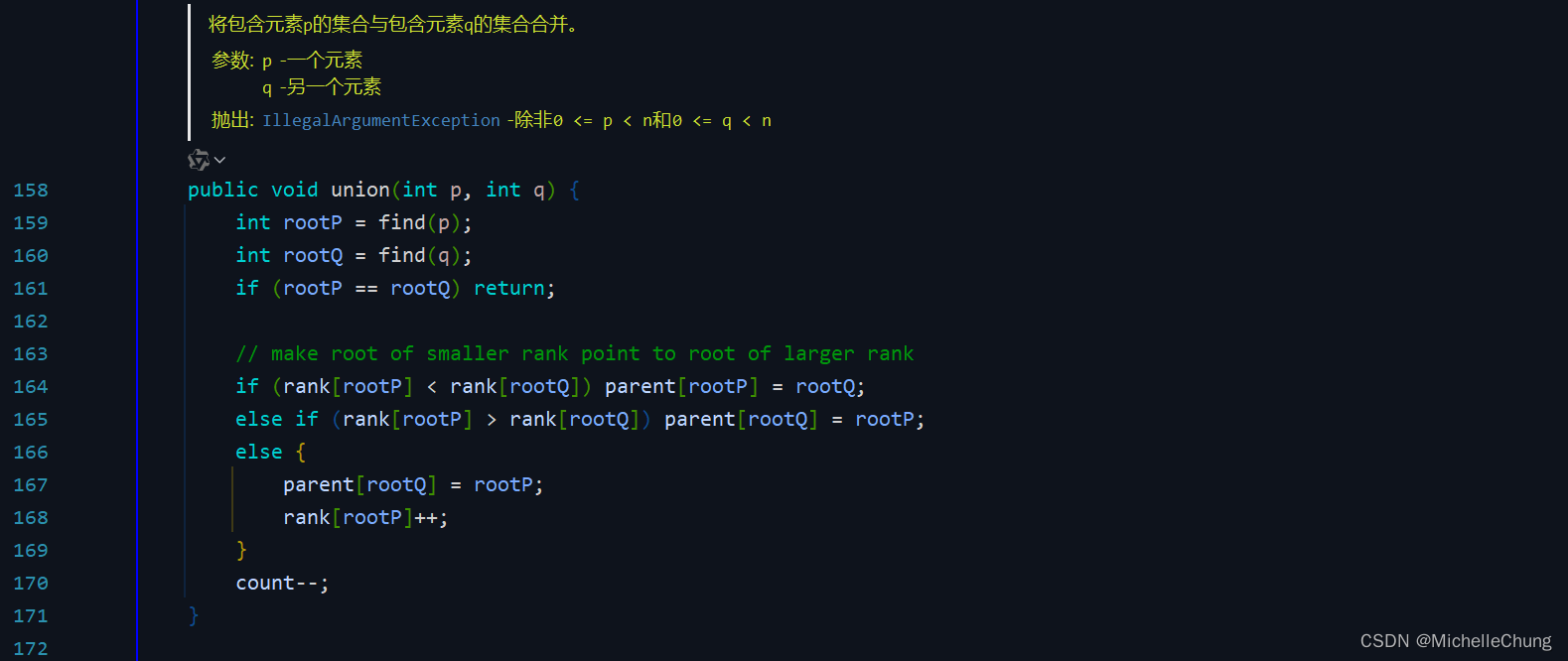
edu.princeton.cs.algs4.UF#union

2：UF 实现 1：快速查找 quick-find

基于数组的实现。

连通性检查：两个下标元素的值是否相同。

2.1：demo 演示 1

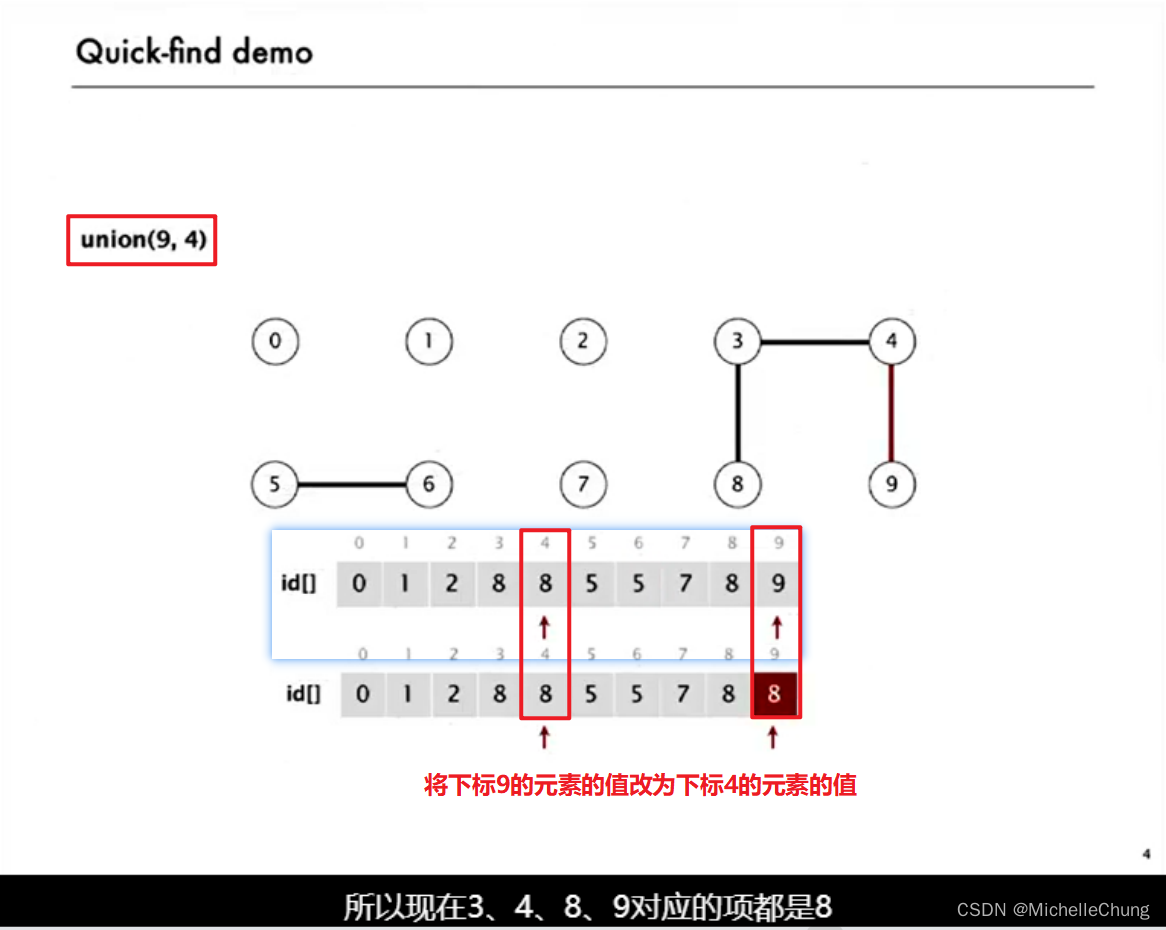
2.2：demo 演示 2

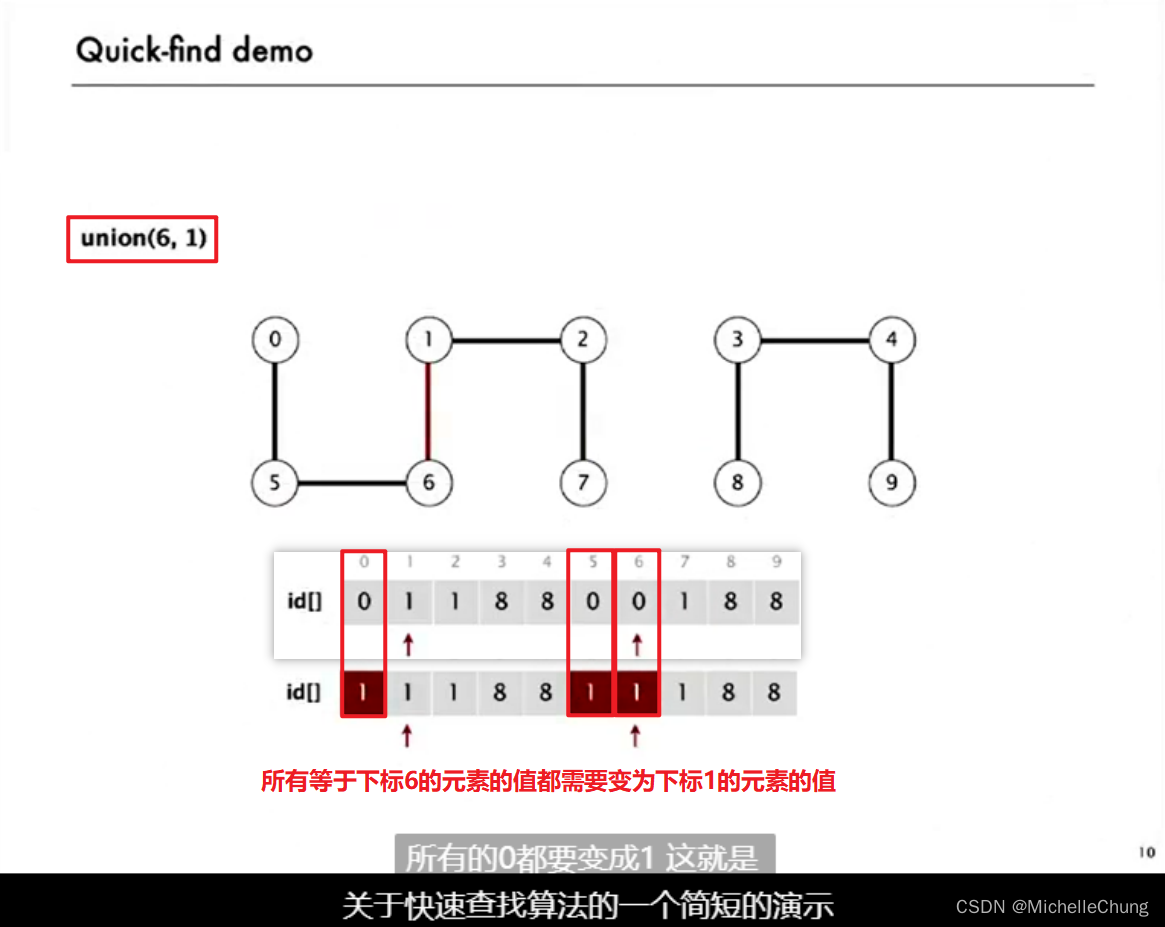
2.3：quick-find 代码实现

edu.princeton.cs.algs4.QuickFindUF#union

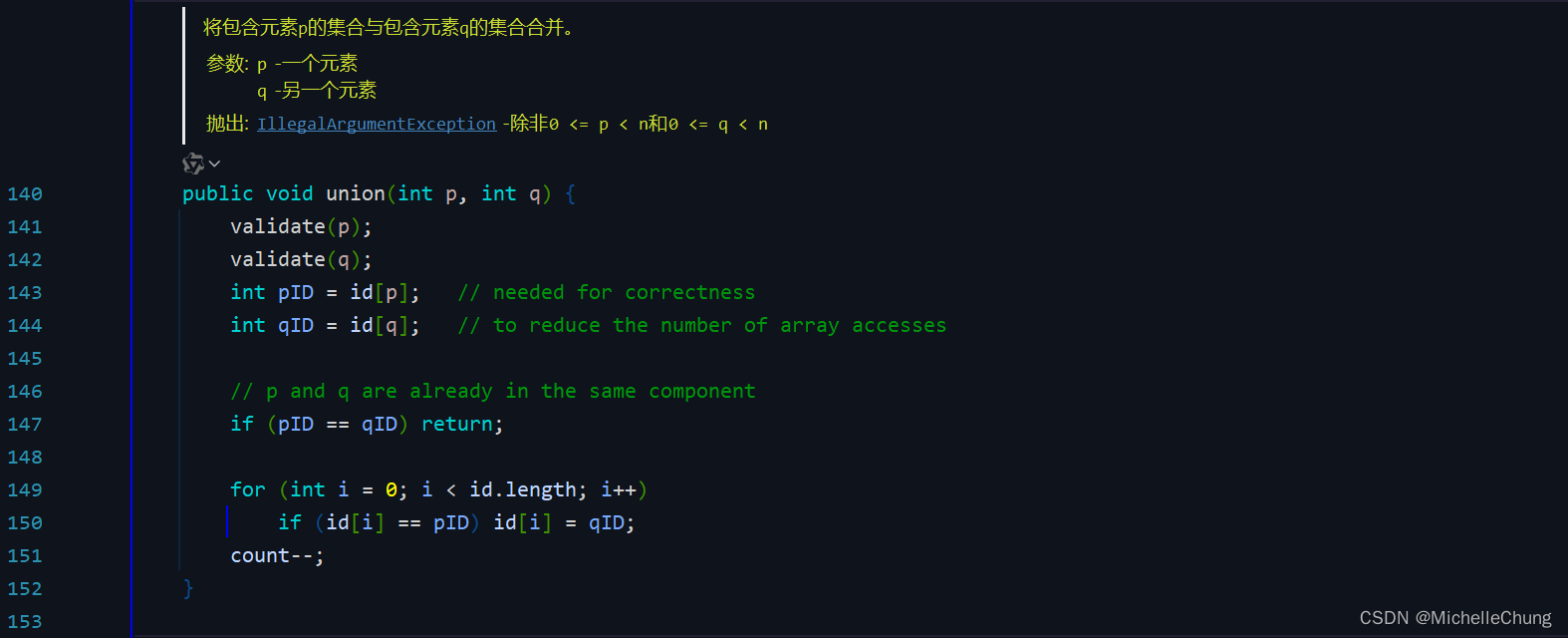
union(p,q)：
将下标为p的元素的值（pID）替换为下标为q的元素的值（qID），且集合中与pID相同的值都需要替换为qID。

3：UF 实现 2：快速合并 quick-union

基于树的实现。

连通性检查：两个下标元素的值的 根节点 是否相同。

3.1：demo 演示 1

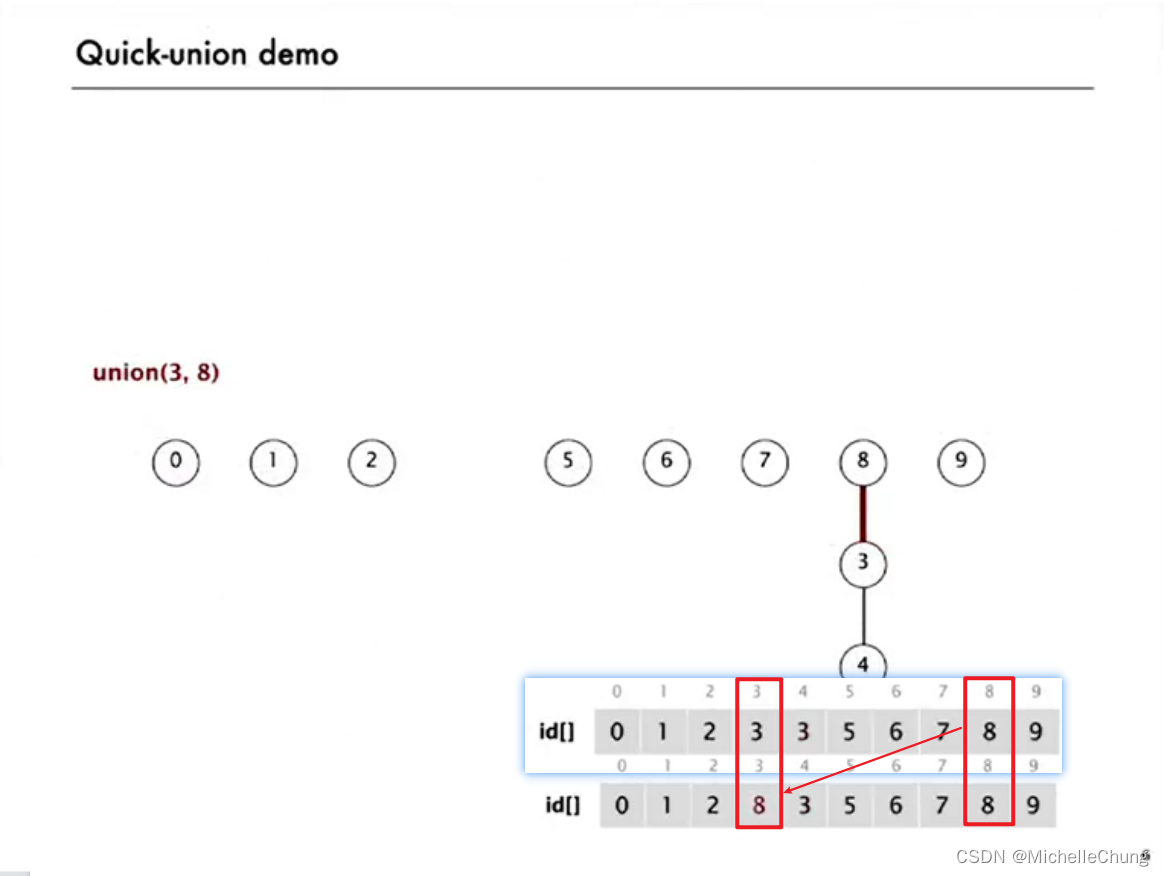
3.2：demo 演示 2

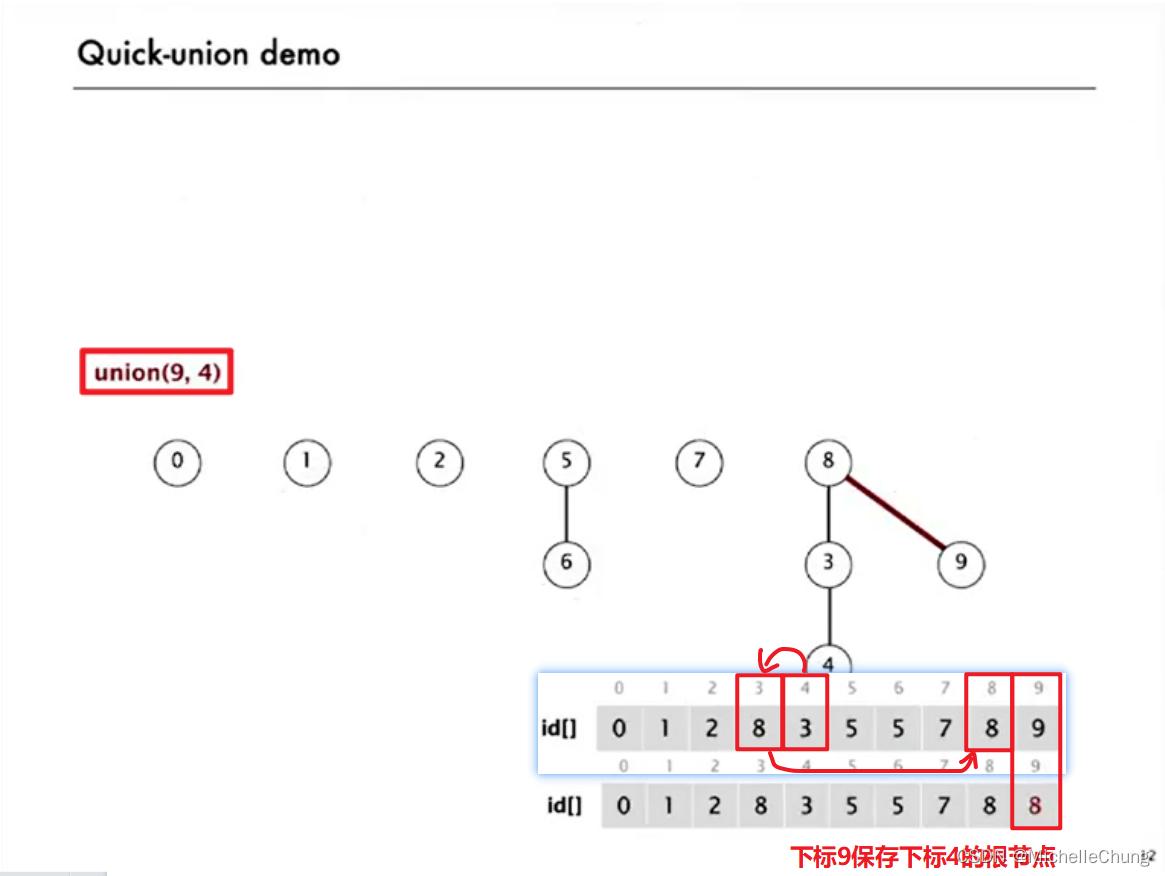
3.3：demo 演示 3

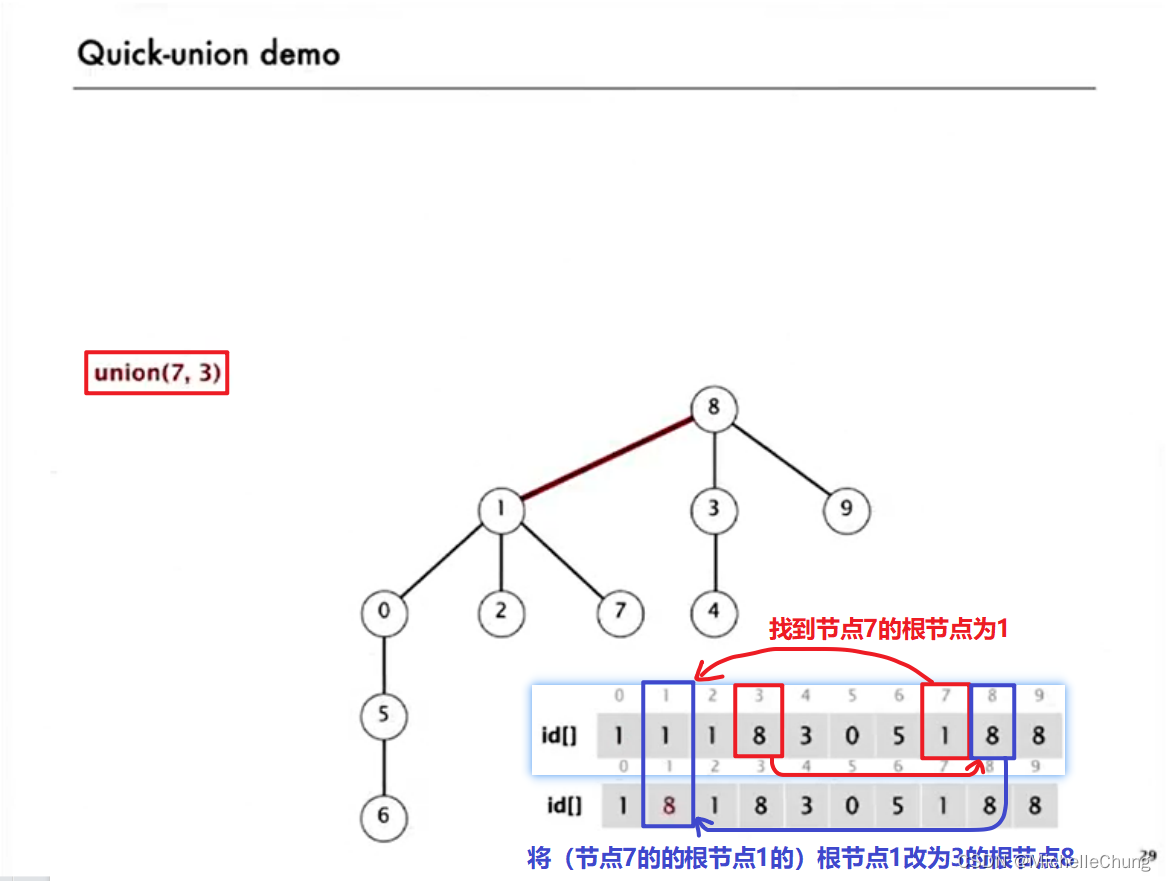
3.4：quick-union 代码实现

edu.princeton.cs.algs4.QuickUnionUF#union

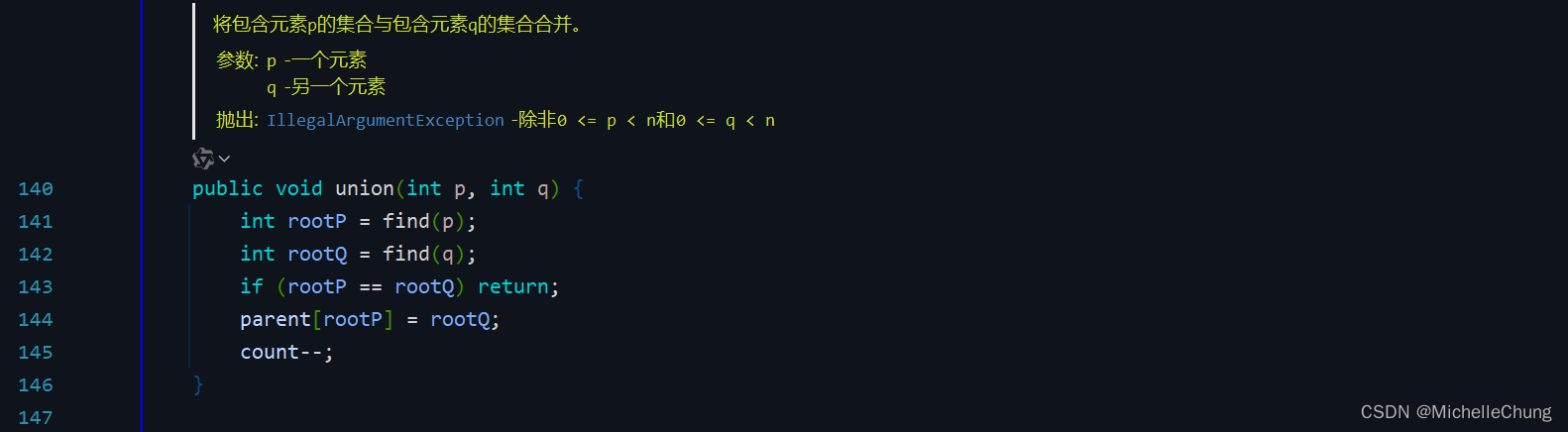
union(p,q)：
将p的根节点改为q的根节点。

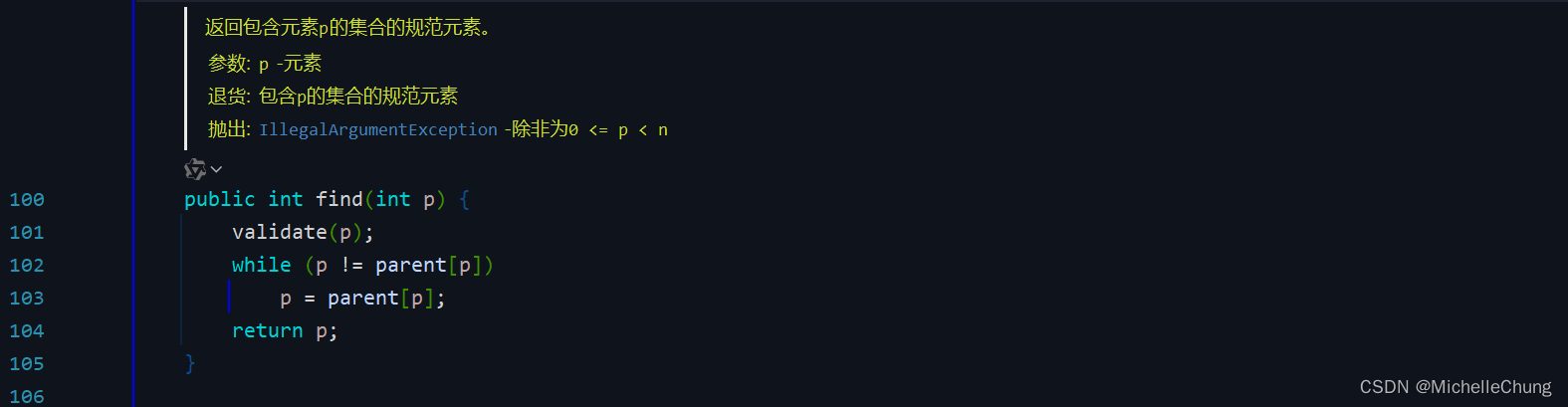
edu.princeton.cs.algs4.QuickUnionUF#find

4：UF 实现 3：加权 quick-union 算法

基于树的实现，对快速合并的优化。

4.1：demo 演示

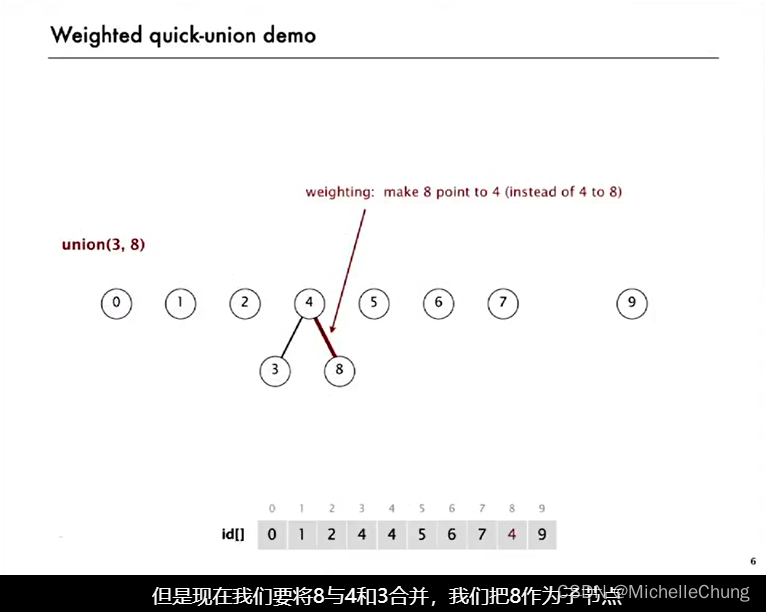
4.2：加权 quick-union 算法代码实现

edu.princeton.cs.algs4.WeightedQuickUnionUF#union

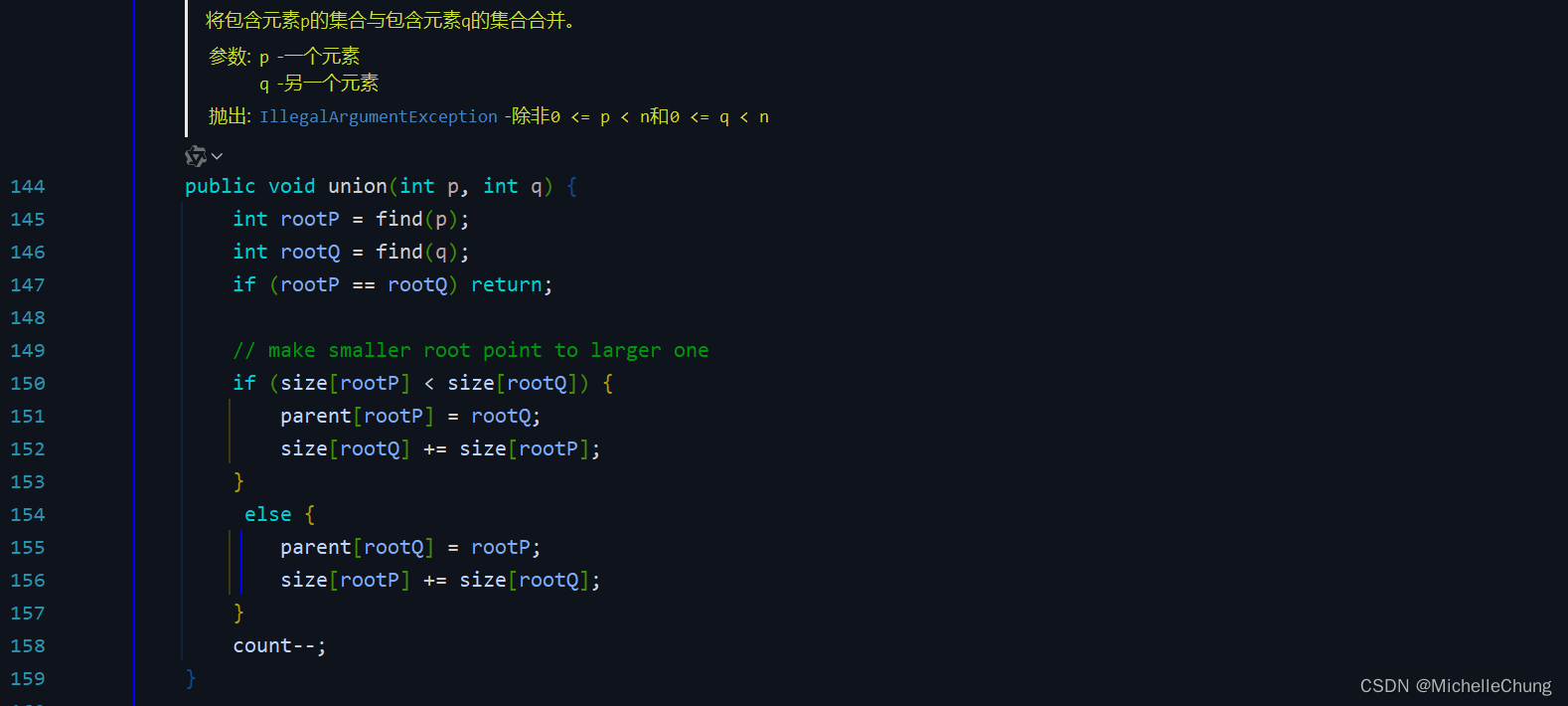
5：带路经压缩的加权 quick-union 算法

这个压缩路径的作用实际上是把树展平，因而在加权 quick-union 算法的基础上只是增加了一行代码即可实现。

配套源码中没有这个算法的源码，教授说这个算法的分析超出了这门课的范围……

6：所有 UF 实现算法的对比

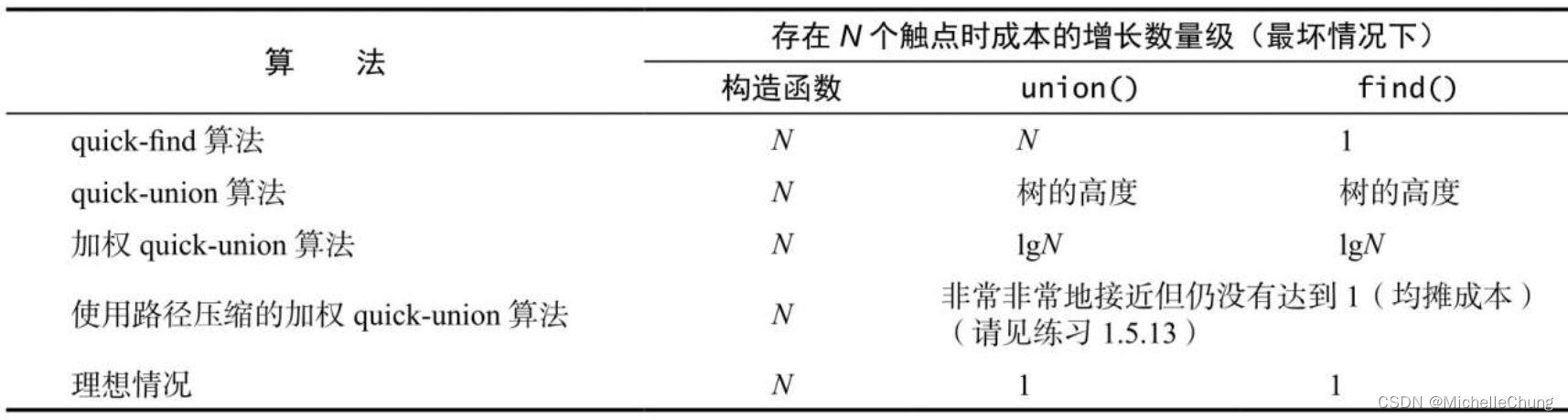
（完）