前言：
算法学习记录不是算法介绍，本文记录的是从零开始的学习过程（见到的例题，代码的理解……），所有内容按学习顺序更新，而且不保证正确，如有错误，请帮助指出。
学习工具：蓝桥OJ，LeetCode
背景知识：
你有动态规划相关基础知识。
（算法学习记录：动态规划基础）
目录
前言：
背景知识：
正文：
模型一：背包问题
01背包：
蓝桥OJ 1174：小明的背包1
蓝桥OJ 2223：背包与魔法
蓝桥OJ 3741：倒水
蓝桥OJ 3637：盗墓分赃
蓝桥OJ 2945：蓝桥课程抢购
完全背包：
蓝桥OJ 1175：小明的背包2
多重背包：
蓝桥OJ 389：摆花
蓝桥OJ 4059：新一的宝藏搜寻加强版
单调队列优化多重背包：
二维费用背包：
蓝桥OJ 3937：小蓝的神秘行囊
分组背包：
蓝桥OJ 1178：小明的背包5
模型二：树型DP
模型三：区间DP
模型四：状压DP
模型五：数位DP
模型六：期望DP
正文：
动态规划：Dynamic Programing 。以下简称“DP”。
按方法分类：搜索法（DFS），迭代法
按实现方式分类：一维DP，二维DP
动态规划涉及的问题种类繁多，按照题目模型分类：
模型一：背包问题
01背包：
问题描述：
有一个体积为V的背包，商店有n个物品，每个物品有一个价值v和体积w，每个物品只能够被拿一次，文能够装下物品的最大价值。
设状态dp[i][j]表示到第i个物品为止，拿的物品总体积为j的情况下的最大价值。
状态转移方程：
蓝桥OJ 1174：小明的背包1
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 105,M = 1010;
ll dp[N][M];
int main()
{
int n,V;cin >> n >> V;
for(int i = 1;i <= n;i ++)
{
ll w,v;cin >> w >> v;
for(int j = 0;j <= V;j ++)
{
if(j >= w)dp[i][j] = max(dp[i-1][j],dp[i-1][j-w]+v);
else dp[i][j] = dp[i - 1][j];
}
}
cout << dp[n][V] << endl;
return 0;
}观察发现：这题我们只关心第n个物品的情况，
所以没必要用二维数组把原来的所有情况存下
每次更新只用上一次数据，如果能直接进行覆盖，就采用一维数组解决问题。
优化：
dp[i][j]=dp[i-1][j]，相当于dp[i-1]复制给dp[i]，
将第一维优化掉直接当作一个数组
每次更新时，从后往前更新，此时dp[j]表示此时物品总体积为j时的物品最大价值。
得到状态转移方程：
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 105,M = 1010;
ll dp[M];
int main()
{
int n,V;cin >> n >> V;
for(int i = 1;i <= n;i ++)
{
ll w,v;cin >> w >> v;
for(int j = V;j >= w;j ++)
{
dp[j] = max(dp[j],dp[j - w] + v);
}
}
cout << dp[V] << endl;
return 0;
}蓝桥OJ 2223：背包与魔法
对每个物品有3种选择：不选、选但不用魔法、选且用魔法
状态转移方程：
#include<iostream>
using namespace std;
using ll = long long;
const int N = 1e4 + 9;
ll dp[N][2];
int main()
{
int n,m,k;cin >> n >> m >> k;
for(int i = 1;i <= n;i ++)
{
ll w,v;cin >> w >> v;
for(int j = m;j >= 0;j --)
{
if(j >= w)
{
dp[j][0] = max(dp[j][0],dp[j - w][0] + v);
dp[j][1] = max(dp[j][1],dp[j - w][1] + v);
}
if(j >= w + k)
{
dp[j][1] = max(dp[j][1],dp[j - w - k][0] + 2 * v);
}
}
}
cout << max(dp[m][0],dp[m][1]) << endl;
return 0;
}蓝桥OJ 3741：倒水
//为了尽可能节约水，本题只有3种倒水方式：
//1、给当前客人倒水a毫升，使得总好感度增加b
//2、给当前客人倒水c毫升(c>a)，使得总好感度增加d
//3、不给客人倒水(对应题目中的倒水小于a毫升，倒与不倒是一样的，还不如不倒)，总好感度增加e
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[1005][1005];//dp[i][j]表示只考虑前i个客人，共倒水j毫升所得的最大好感度
//易知对于第i个客人，给其倒水所得好感度的多少只与前i-1个客人有关
int main()
{
int N,M;
cin>>N>>M;
for(int i=1;i<=N;i++)//分别考虑前1~N个客人
{
ll a,b,c,d,e;
cin>>a>>b>>c>>d>>e;
for(int j=0;j<=M;j++)//对第i个客人，分别考虑共倒0~M毫升水
{
//若当前拥有的水小于a，干脆不倒水，好感度为前i-1个客人共倒j升水所得好感度 加上e
if(j<a)dp[i][j]=dp[i-1][j]+e;
//若当前拥有的水不小于a但是小于c，则可以选择倒a毫升或者不倒水
//若倒a毫升水，则好感度为 前i-1个客人共倒j-a毫升水所得好感度 加上b
//若不倒水，则好感度为 前i-1个客人共倒j毫升水所得好感度 加上e
//二者取较大值即可
else if(j>=a&&j<c)dp[i][j]=max(dp[i-1][j-a]+b,dp[i-1][j]+e);
//若当前拥有的水足够多，依次考虑三种情况，同理可得
else dp[i][j]=max(dp[i-1][j-a]+b,max(dp[i-1][j-c]+d,dp[i-1][j]+e));
}
}
cout<<dp[N][M]<<endl;//考虑前N个客人，共倒M毫升水所得好感度的最大值 即为最终答案
return 0;
}优化：
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll dp[1005];
int main()
{
int N,M;
cin>>N>>M;
for(int i=1;i<=N;i++)
{
ll a,b,c,d,e;
cin>>a>>b>>c>>d>>e;
for(int j=M;j>=0;j--)
{
if(j<a)dp[j]=dp[j]+e;
else if(j>=a&&j<c)dp[j]=max(dp[j-a]+b,dp[j]+e);
else dp[j]=max(dp[j-a]+b,max(dp[j-c]+d,dp[j]+e));
}
}
cout<<dp[M]<<endl;
return 0;
}蓝桥OJ 3637：盗墓分赃
#include<bits/stdc++.h>
using namespace std;
const int N=2e4+5;
bool dp[N];
const int M=1e3+4;
int s[M];
int main()
{
int n;cin>>n;
int sum=0;
for(int i=1;i<=n;i++)
{
cin>>s[i];
sum+=s[i];
}
dp[0]=true; //啥也不拿一定可以
if(sum%2!=0)
cout<<"no"<<'\n';
else
{
for(int i=1;i<=n;i++)
{
for(int j=sum;j>=1;j--)
{
if(j>=s[i])
dp[j]=dp[j]||dp[j-s[i]];
}
}
if(dp[sum/2])
cout<<"yes"<<'\n';
else
cout<<"no"<<'\n';
}
return 0;
}蓝桥OJ 2945：蓝桥课程抢购
由于要先考虑把时间短的放前面，使用结构体数组把数据关联起来，便于操作。
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+4;
ll dp[55][N]; //表示在i个科目之前，j的等待时间下最大的价值
struct Class
{
int wait,j,value;
}c[55];
bool cmp(Class a,Class b)
{
return a.j<b.j;
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n;cin>>n;
int sum=0;
for(int i=1;i<=n;i++)
{
cin>>c[i].wait>>c[i].j>>c[i].value;
sum=max(sum,c[i].j);
}
sort(c+1,c+n+1,cmp); //先把截至时间短的放前面,贪心把时间短的先做了
ll ans=0;
for(int i=1;i<=n;i++)
{
for(int j=sum;j>=1;j--)
{
dp[i][j]=dp[i-1][j]; //先初始化成这个科目不选
if(j>=c[i].wait&&j<=c[i].j)
{
dp[i][j]=max(dp[i][j],dp[i-1][j-c[i].wait]+c[i].value);
ans=max(ans,dp[i][j]);
}
}
}
cout<<ans<<'\n';
return 0;
}优化：
#include<bits/stdc++.h>
using namespace std;
using ll=long long;
const int N=1e5+4;
ll dp[N]; //表示在i个科目之前，j的等待时间下最大的价值
struct Class
{
int wait,j,value;
}c[55];
bool cmp(Class a,Class b)
{
return a.j<b.j;
}
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n;cin>>n;
int sum=0;
for(int i=1;i<=n;i++)
{
cin>>c[i].wait>>c[i].j>>c[i].value;
sum=max(sum,c[i].j);
}
sort(c+1,c+n+1,cmp); //先把截至时间短的放前面,贪心把时间短的先做了
ll ans=0;
for(int i=1;i<=n;i++)
{
for(int j=sum;j>=1;j--)
{
dp[j]=dp[j]; //先初始化成这个科目不选
if(j>=c[i].wait&&j<=c[i].j)
{
dp[j]=max(dp[j],dp[j-c[i].wait]+c[i].value);
ans=max(ans,dp[j]);
}
}
}
cout<<ans<<'\n';
return 0;
}完全背包：
又名无穷背包，每种物品有无数个背包。
即每个物品可以被拿无数次，有无限多个。
设状态dp[i]表示拿的物品总体积为i的情况下的最大价值。
状态转移方程：
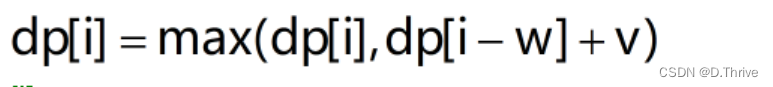
因为新数据的产生必须有先后，现在就必须用”新数据“来更新“新数据”。
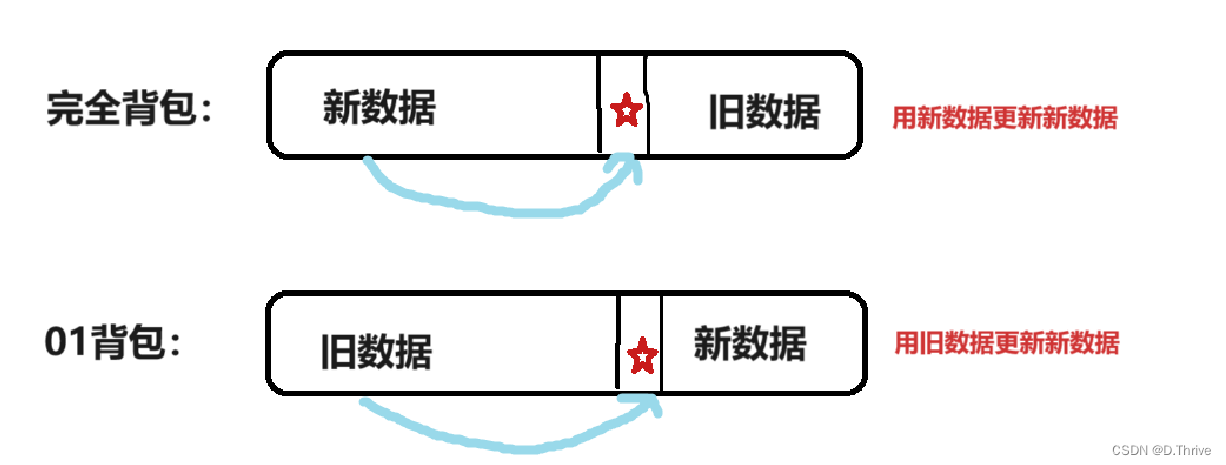
蓝桥OJ 1175：小明的背包2
#include<iostream>
using namespace std;
const int N = 1e3 + 9;
int dp[N];
int main()
{
int n,m;cin >> n >> m;
for(int t = 1;t <= n;t++)
{
int w,v;cin >> w >> v;
for(int i = w;i <= m;i ++)
{
dp[i] = max(dp[i],dp[i - w] + v);
}
}
cout << dp[m];
return 0;
}对比这题与’小明的背包1‘，
可以发现：遍历顺序变化后，
dp[i]可以来自在相同t情况（遍历到了同一件物品）下刚刚被更新过的数据 。
这就计算了这件物品可以被用多次的情况。
多重背包：
有一个体积为V的背包，商店有n种物品，每种物品有一个价值v和体积w，每种物品有s个，问装下的最大价值。
只需在01背包模型的基础上再加一层循环，更新s次即可。
蓝桥OJ 389：摆花
对于每一个到达一个位置并种了某种花的情况，
方案数都是先种上一个位置并种了少用一种花的方案数，
具体来说：
这个方案数就是：保持种到相同位置，这最后一种花种了多少盆的所有情况的方案数之和
设状态dp[i][j]表示到第i种花为止（不一定以第i种花结尾），到第j个位置（1-j都放了花）的情况下的总方案数：
图解：
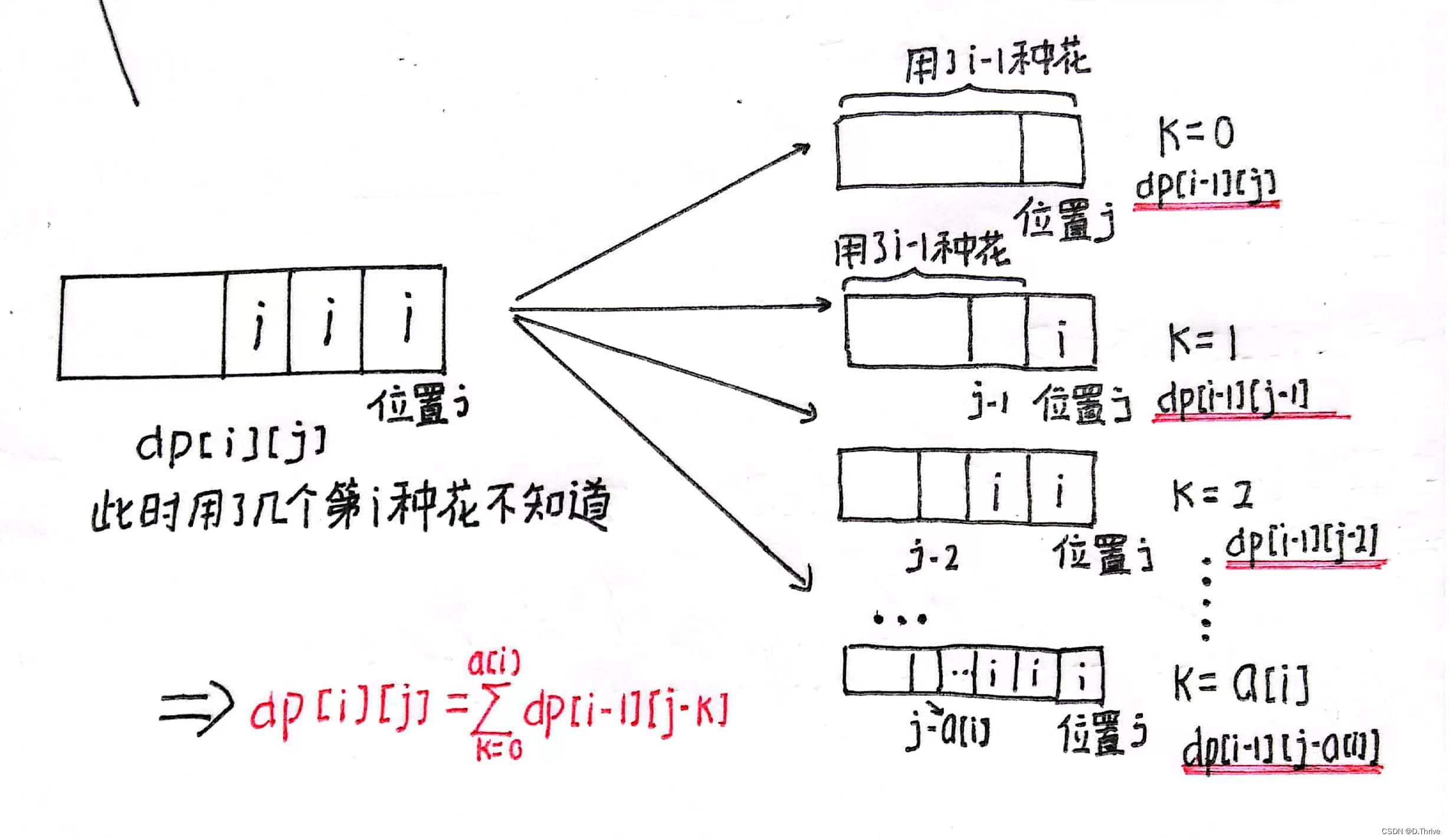
归纳出状态转移方程：
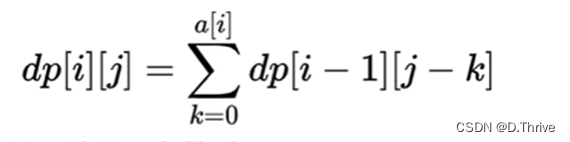
#include<bits/stdc++.h>
using namespace std;
const int N = 105;
using ll = long long;
const ll p = 1e6 + 7;
ll a[N],dp[N][N];
int main()
{
int n,m; cin >> n >> m;
for(int i = 1;i <= n; i ++)cin >> a[i];
dp[0][0] = 1;
for(int i = 1;i <= n;i ++)
{
for(int j = 0;j <= m;j ++)
{
for(int k = 0;k <= a[i] && k <= j; k ++){
dp[i][j] = (dp[i][j] + dp[i - 1][j - k]) % p;
}
}
}
cout << dp[n][m] << endl;
return 0;
}蓝桥OJ 4059：新一的宝藏搜寻加强版
#include<iostream>
using namespace std;
const int N = 205;
int dp[N];
int main()
{
int n,m;cin >> n >> m;
for(int i = 1;i <= n;i ++)
{
int w,v,s;cin >> w >> v >> s;
while(s--)
{
for(int j = m;j >= w;j--)
{
dp[j] = max(dp[j],dp[j - w] + v);
}
}
}
cout << dp[m] << endl;
return 0;
}优化：原时间复杂度：O（n*s*V）
进行二进制优化：时间复杂度：O（n*logs*V）
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1e3+7,M = 2e4 +7;
ll dp[M];
int main()
{
ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
int n,m;cin >> n >> m;
for(int i = 1;i <= n;i ++)
{
ll v,w,s;cin >> v >> w >> s;
for(int k = 1;k <= s;s -= k,k +=k)
{
for(int j = m;j >= k * v;j--)dp[j] = max(dp[j],dp[j - k * v] + k * w);
}
for(int j = m;j >= s*v;j --)dp[j] = max(dp[j],dp[j - s * v]+ s* w);
}
cout << dp[m] << endl;
return 0;
}单调队列优化多重背包：
另见：算法学习记录：滑动窗口
优化效果（时间复杂度）：
二维费用背包：
问题描述：
有一个体积为V的背包，商店有n种物品，每种物品有一个价值v、体积w、重量m，每种物品仅有1个，问能装下物品的最大价值。（需同时考虑体积和重量限制）
倒着更新，状态转移方程修改成二维。
状态转移方程：
蓝桥OJ 3937：小蓝的神秘行囊
#include<bits/stdc++.h>
using namespace std;
using ll = long long ;
const int N = 105;
ll dp[N][N];
int main()
{
int n,V,M;cin >> n >> V >> M;
for(int i = 1;i <= n;i ++)
{
int v,m,w;cin >> v >> m >> w;
for(int j = V;j >= v;-- j)
{
for(int k = M;k >= m;k--)
{
dp[j][k] = max(dp[j][k],dp[j-v][k-m] + w);
}
}
}
cout << dp[V][M] << endl;
return 0;
}分组背包：
有一个体积为V的背包，商店有n组物品，每组物品有若干个，价值v、体积w。每组物品至多选一个，问能够装下的最大价值。
设状态dp[i][j]表示到第i组，体积为j的最大价值，这里不能忽略第一维，否则状态转移错误。
状态转移方程：
蓝桥OJ 1178：小明的背包5
#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 1500;
ll dp[N][N];
int main()
{
int n,V;cin >> n >> V;
for(int i = 1;i <= n;i ++)
{
int s;cin >> s;
for(int j = 0;j <= V;j ++)dp[i][j] = dp[i - 1][j];
while(s --)
{
ll w,v;cin >> w >> v;
for(int j = w;j <= V;j ++)dp[i][j] = max(dp[i][j],dp[i - 1][j - w] + v);
}
}
cout << dp[n][V] << endl;
return 0;
}模型二：树型DP
了解过了树的基础后：算法学习记录：有关树的基础
自上而下DP：
考虑树型DP问题一：
如果暴力枚举：时间复杂度为O(n*2^n）不能解决问题
考虑贪心的办法：发现即使使用最大权值和作为判断依据，难以对树状结构进行正确计算。
因此采用动态规划算法：
考虑状态：
由题中限制：一个子结点能不能选，受上一个结点的约束
所以需要开二维dp，用0或1表示被选或未被选的状态。
用f[i][0]表示当前结点不选所能得到的最大值
用f[i][1]表示当前结点选择后所能得的最大值。
考虑转移：
自上而下转移：在结点的所有儿子结点中取最大值，对0/1的情况分类讨论。
归纳出状态转移方程：
#include <bits/stdc++.h>
using namespace std;
#define maxn 110000
int n, val[maxn];
struct Edge
{
int nex, to;
}edge[maxn << 1];
int head[maxn], cnt;
int f[maxn][2];
void add(int from, int to)
{
edge[++cnt].nex = head[from];
head[from] = cnt;
edge[cnt].to = to;
return ;
}
void dfs(int u, int fa)
{
for (int i = head[u]; i; i = edge[i].nex)
{
int v = edge[i].to;
if (v != fa)
continue;
dfs(v, u);
f[u][0] += max(f[v][0], f[v][1]);
f[u][1] += f[v][0];
}
return ;
}
int main()
{
scanf("%d", &n);
for (int i = 1; i <= n; ++ i )
scanf("%d", &val[i]), f[i][1] = val[i];
for (int i = 1; i < n; ++ i )
{
int u, v;
scanf("%d%d", &u, &v);
add(u, v), add(v, u);
}
dfs(1, 0);
printf("%d\n", max(f[1][0], f[1][1]));
return 0;
}考虑树型DP问题二：
考虑状态：
承接上一个模型，会想到用一个三维的dp，
仔细观察发现，可以将根据体积关系优化掉0/1这一维。
图解：
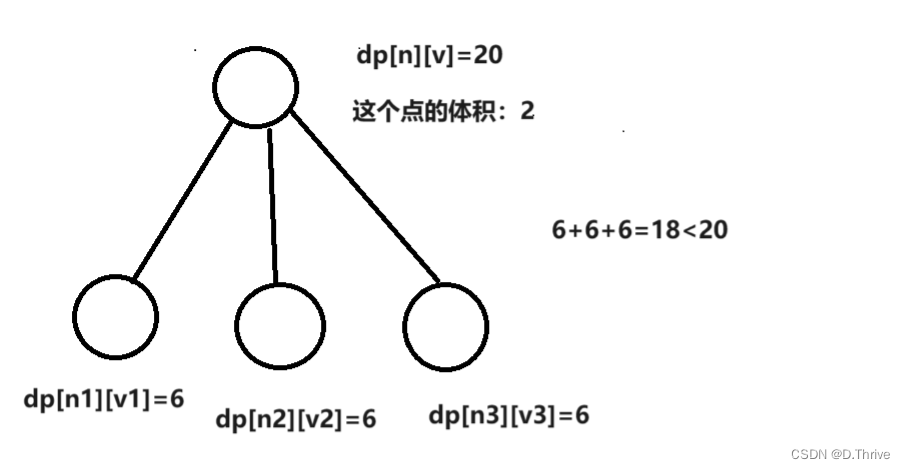
由体积的数量关系可以判断这个父结点一定被选上了，这样实现了一维的优化。
考虑转移：
在每一个结点下，把它的所有子节点当作许多物品。
用01背包的思路，将“贡献”合并。
归纳出状态转移方程：
这是最核心的部分：
1.需要开一个新的一维数组来存储临时情况，因为更新时会用到原数据，不可以直接覆盖。
2.外层循环会遍历到每个子节点，所以对于数组nf[v]，最后复制回f[u][v]的数据是遍历过所有子结点的最终数据，是每个体积下的合法最优状况。
#include <bits/stdc++.h>
using namespace std;
#define maxn 110
int n, V;
int f[maxn][maxn];
int w[maxn], v[maxn];
vector<int> g[maxn];
struct Edge
{
int nex, to;
}edge[maxn << 1];
int head[maxn], cnt;
void add(int from, int to)
{
edge[++ cnt].nex = head[from];
head[from] = cnt;
edge[cnt].to = to;
return ;
}
void dfs(int u, int fa)
{
memset(f[u], -0x3f, sizeof f[u]);
if (v[u] <= V)
f[u][v[u]] = w[u];
for (int i = head[u]; i; i = edge[i].nex)
{
int v = edge[i].to;
if (v == fa)
continue;
dfs(v, u);
vector<int> nf(f[u], f[u] + V + 1);
for (int v1 = 0; v1 <= V; v1 ++)
{
for (int v2 = 0; v1 + v2 <= V; v2 ++ )
{
nf[v1 + v2] = max(nf[v1 + v2], f[u][v1] + f[v][v2]);
}
}
for (int v = 0; v <= V; v ++ )
f[u][v] = nf[v];
}
return ;
}
int main()
{
scanf("%d%d", &n, &v);
for (int i = 1; i < n; ++ i )
{
int u, v;
add(u, v), add(v, u);
}
dfs(1, 0);
int ans = 0;
for (int i = 0; i <= V; ++ i )
ans = max(ans, f[1][i]);
cout << ans << endl;
return 0;
}
自下而上DP：
每一次进行转移时，先遍历子节点，求出子节点的DP值之后，再向父节点转移。
最大独立集：
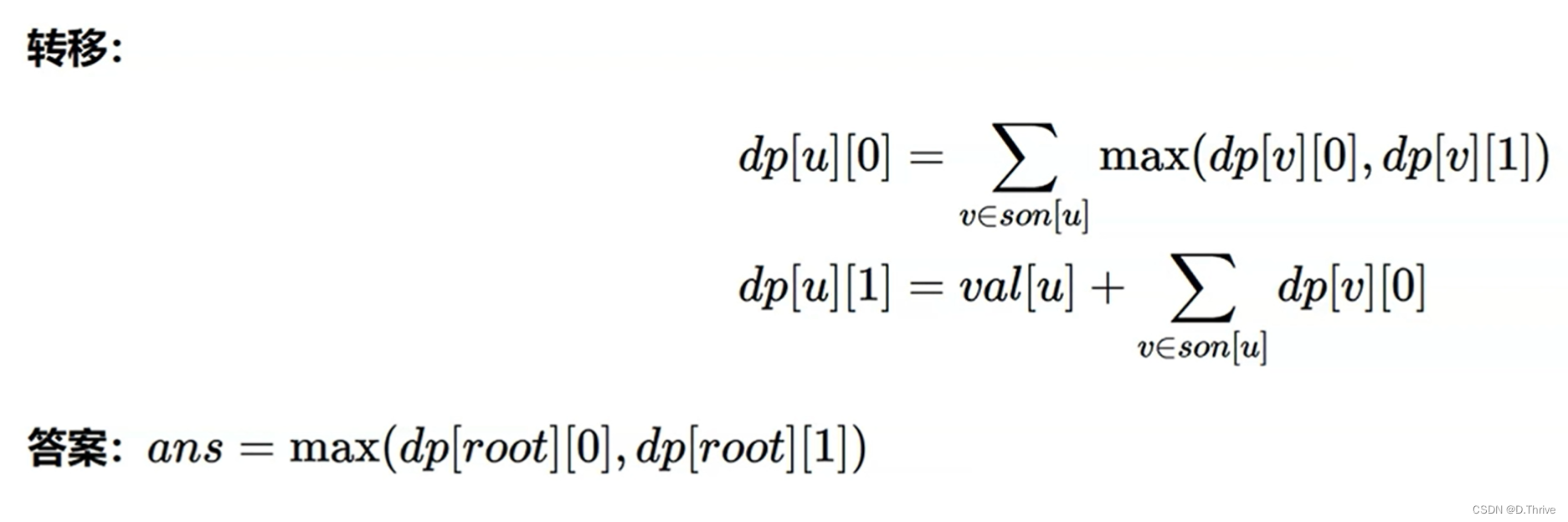蓝桥OJ 1319：蓝桥舞会
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
int n,a[N];
long long dp[N][2];
vector<int> e[N];
void dfs(int u)
{
for (auto v:e[u])
{
dfs(v);
dp[u][1]+=dp[v][0];
dp[u][0]+=max(dp[v][0],dp[v][1]);
}
dp[u][1]+=a[u];
}
int main()
{
cin>>n;
set<int> st;
for (int i=1;i<=n;i++) cin>>a[i],st.insert(i);
for (int i=1,x,y;i<n;++i)
{
cin>>x>>y;
e[y].push_back(x);
st.erase(x);
}
int rt=*st.begin();
dfs(rt);
cout<<max(dp[rt][0],dp[rt][1]);
return 0;
}最小点覆盖：
选择若干个点，使得树上每一条边都被覆盖。
即每一条边都至少有一个端点被选择，求被选择的点权和的最值。
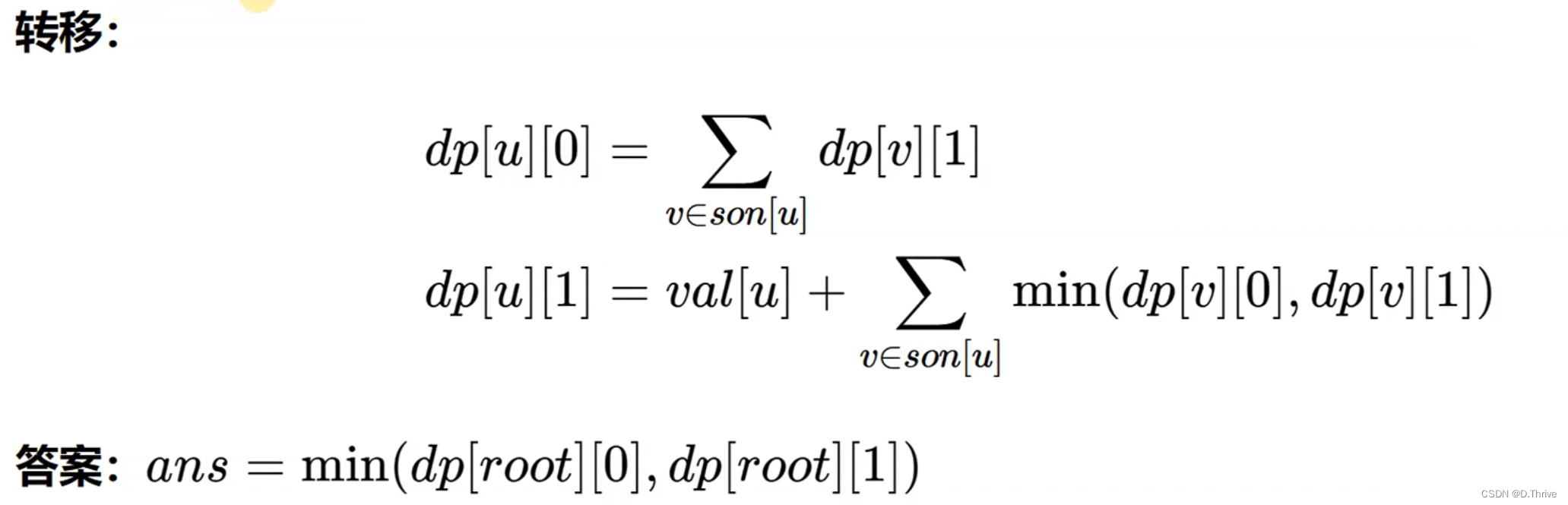
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
vector<int>e[N];
int val[N],dp[N][2];
int d[N];
int n, m, k;
void dfs(int u,int fa)
{
for (auto v:e[u])
{
if (v==fa) continue;
dfs(v,u);
dp[u][0]+=dp[v][1];
dp[u][1]+=min(dp[v][0],dp[v][1]);
}
dp[u][1]+=1;
}
int main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin>>n;
for (int i=1,x,y;i<n;++i)
{
cin>>x>>y;
e[x].push_back(y);
e[y].push_back(x);
}
dfs(1,0);
cout<<min(dp[1][0],dp[1][1]);
return 0;
}最小支配集：
选择若干个点，使得树上的每一个点都被支配，即每一点要么自身被选择要么相邻的结点被选择。
求选择的点的点权和最值。
模型三：区间DP
区间DP是以区间为尺度的DP，一般有以下特点：
1.可以将一个大区间的问题拆成若干个子区间合并的问题
2.两个连续的子区间可以进行整合、合并成一个大区间。
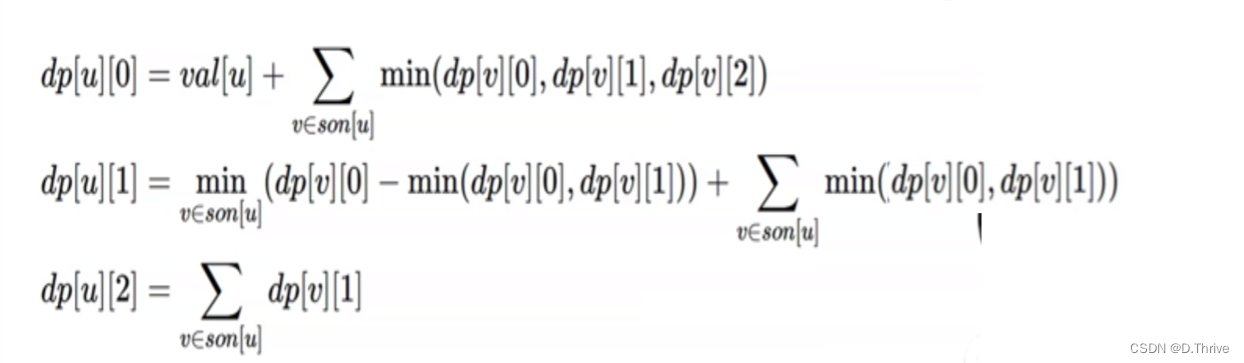
模型题：
#include <bits/stdc++.h>
using namespace std;
const int N=100005;
vector<int>e[N];
long long a[N],dp[N][3];
int d[N];
int n;
void dfs(int u)
{
long long minn=1e18;
for (auto v:e[u])
{
dfs(v);
dp[u][0]+=min({dp[v][0],dp[v][1],dp[v][2]});
dp[u][1]+=min(dp[v][0],dp[v][1]);
minn=min(minn,dp[v][0]-min(dp[v][0],dp[v][1]));
dp[u][2]+=dp[v][1];
}
dp[u][0]+=a[u];
dp[u][1]+=minn;
}
int main()
{
cin.tie(0);
cout.tie(0);
ios::sync_with_stdio(0);
cin>>n;
for (int i=1;i<=n;++i)
{
int id,m;
cin>>id;
cin>>a[id];
cin>>m;
while (m--)
{
int x;
cin>>x;
e[id].push_back(x);
d[x]++;
}
}
int rt;
for (int i=1;i<=n;++i)
if (d[i]==0) rt=i;
dfs(rt);
cout<<min(dp[rt][0],dp[rt][1]);
return 0;
}
