例题 28. 找出字符串中第一个匹配项的下标

暴力遍历解法

枚举原串 ss 中的每个字符作为「发起点」，每次从原串的「发起点」和匹配串的「首位」开始尝试匹配： 匹配成功：返回本次匹配的原串「发起点」。 匹配失败：枚举原串的下一个「发起点」，重新尝试匹配。

时间复杂度: O(mn)

空间复杂度: O(1)

class Solution {
public:
    int strStr(string s, string p) {
        int n = s.size(), m = p.size();
        for(int k = 0; k <= n - m; k++){
            int i, j = 0; 
            while(j < m and s[k + i] == p[j]){
                j++; i++;
            }
            if(j == m) return i + k;
        }
        return -1;
    }
};

KMP

还有一种专门的方案KMP，时间复杂度O(m+n)。

很多讲解方案尤其复杂，这里只需要简单的理解一个东西就豁然开朗原理，无需背代码，在应试时候可以现场推导原理。

字符串前缀与后缀

首先理解字符串的前缀和后缀。

例如，”Harry”的前缀包括{”H”, ”Ha”, ”Har”, ”Harr”}，我们把所有前缀组成的集合，称为字符串的前缀集合。”Potter”的后缀包括{”otter”, ”tter”, ”ter”, ”er”, ”r”}，然后把所有后缀组成的集合，称为字符串的后缀集合。

要注意的是，字符串本身并不是自己的前缀或者后缀。

部分匹配表(Partial Match Table)

前面介绍字符串的前缀和后缀有什么用呢？是因为KMP算法的核心数据结构部分匹配表PMT用到了字符串的前缀集合与后缀集合。

首先给出一个定义1：PMT中的值是字符串的前缀集合与后缀集合的交集中最长元素的长度。（请读三遍理解并深刻记住这个定义）

以下讲解将使用例子：主字符串ababababca中查找模式字符串abababca。

例如，对于”aba”，它的前缀集合为{”a”, ”ab”}，后缀 集合为{”ba”, ”a”}。两个集合的交集为{”a”}，那么长度最长的元素就是字符串”a”了，长 度为1，所以对于”aba”而言，它在PMT表中对应的值就是1。

再比如，对于字符串”ababa”，它的前缀集合为{”a”, ”ab”, ”aba”, ”abab”}，它的后缀集合为{”baba”, ”aba”, ”ba”, ”a”}， 两个集合的交集为{”a”, ”aba”}，其中最长的元素为”aba”，长度为3。所以对于”ababa”而言，它在PMT表中对应的值就是1。

这里也先看一个PMT表关于模式字符串abababca``的例子（这里暂时不需要理解，看一下数据结构长什么样子）。

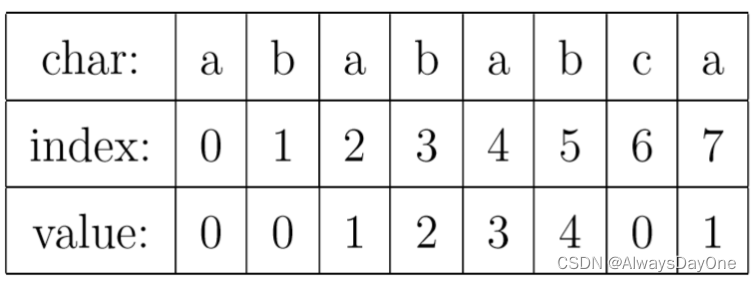
接下来就是KMP算法的核心：如何利用定义1简化暴力双循环的搜索方法：

• 在暴力双循环中定义了i j 指针分别指向待匹配字符串str 和 匹配字符串match ，若位置str[i+k] 和 match[j] 匹配失败时，丢弃已匹配成功的 match[0,j)字符串
• 注意到已匹配成功的match[0,j)字符串其实是有用的，这里可以进行优化。
• 目前匹配的字符串中， 从str[k, i+k） 得到后缀集合postfix_str, 从match[0,j） 得到前缀集合prefix_match，然后求两个集合的交集中最长的字符串 sub_str
• 关键原理1：这个字符串 sub_str就是暴力双循环从 i+1 位置重新遍历到当前 i+j 位置时候匹配得到的最长字符串。
  • 以下图为例，a中在j = 6 处匹配失败，那么如果暴力循环就是i 回到k，j 回到0重新开始匹配，最终i又走到6这个位置的时候，最长匹配的一次是str[2,6]的字符串
  • KMP的前后缀集合重合的最长字符串，就是意味着在待匹配字符串str 中从i 回溯到k位置的后缀中与匹配字符串match匹配上最长的一次。
    

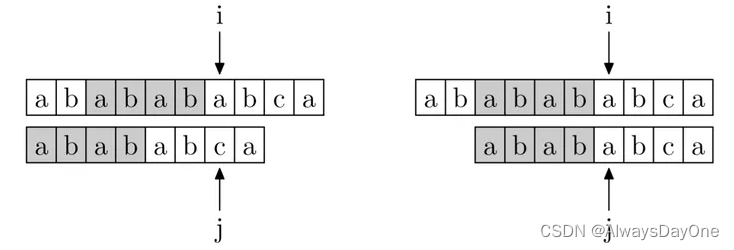
有了如上的发现可以快速的回溯指针并省略一些遍历，但怎么快速的匹配前缀与后缀呢。下面关键原理2将解释如何做到这个快速回溯。

• 关键原理2：可以发现match在j位置匹配失败了，match[0,j) 与 str[k,k+i)是完全相同的，则后缀集合postfix_str与前缀集合prefix_match实际都可以从 match[0,j) 数组来得到 。而match数组是遍历前就确定的，则遍历之前就可以通过match数组得到这个快速回溯的地址。

  • 看到这，你就明白了KMP的核心数据结构 部分匹配表PMT ,按照这个思路求出例子中的PMT表

  • 

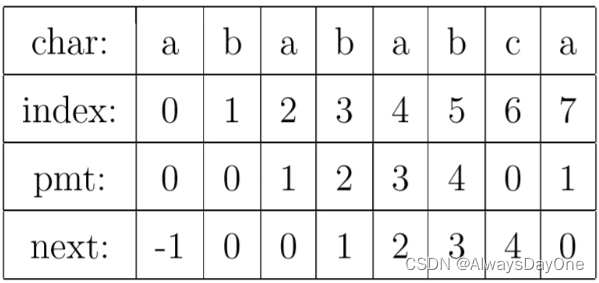
  • 其中 **next 数组就是在当前位置匹配失败后可以直接将j指针跳到哪个位置，代表 str[k, k+i) 和 match[0,j） 又匹配上了。**其中 -1 是第一个位置都匹配不上，i j都需要移动，而其他的都是匹配失败后只移动了j到next[j]

具体程序为：

int KMP(string haystack, string needle)
    {
        int n = haystack.size(), m = needle.size();
        vector<int> next = getNext(needle);
        // ij两个指针分别指向被匹配字符串和模式字符串的已成功匹配位置
        int i = 0, j = 0; 
        // 遍历整个被匹配字符串比对 或 匹配成功 结束循环
        while (i < n && j < m)
        {
            // 初始匹配位置 或 当前指针位置匹配成功
            if (j == -1 || haystack[i] == needle[j])
            {
                j++;
                i++;
            }
            else j = next[j];
        }
        if (j == m) return i - j;
        return -1;
    }

好了，KMP的主体原理就讲完了。这里你会发现KMP的核心思想就是从前后缀集合最长公共字符串而来。

Next 数组快速推导

另一方面首先需要得到PMT 中的核心数据结构Next数组，这里也有一定的技巧帮助我们快速得到。

具体来说，就是从模式字符串的第一位开始对自身进行匹配运算(注意，不包括第0位，因为第0位就匹配失败的next值为-1)。 在任一位置，能匹配的最长长度就是当前位置的next值。

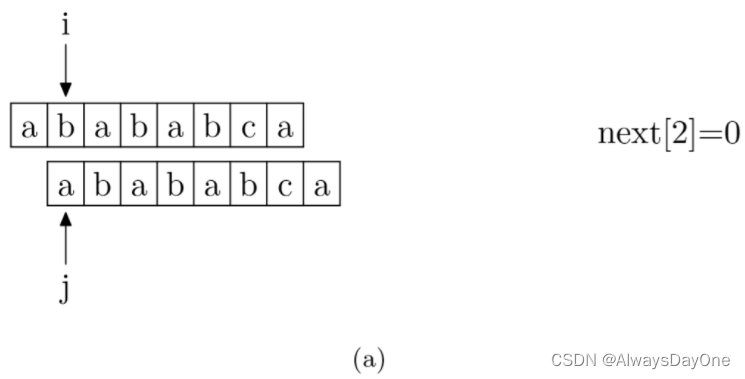
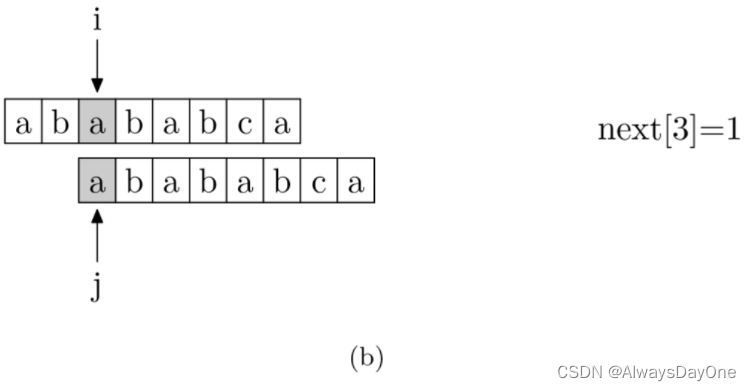
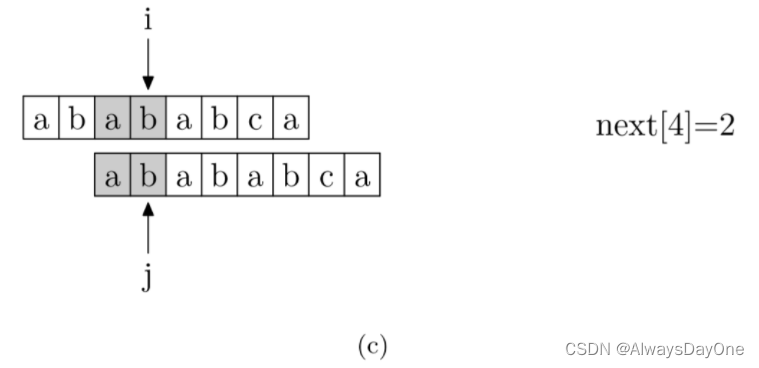
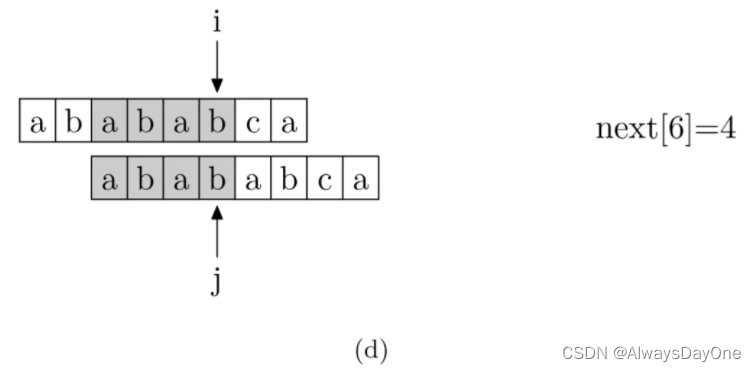
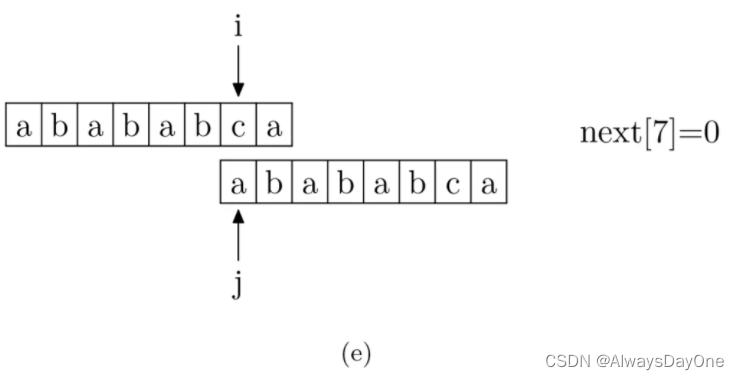
在next数组求取的时候，其实就是以match[0,i]的字符串后缀与match[0,j]的字符串前缀匹配。注意：那么当匹配失败可以快速的使用next数组，相当于递归的使用了KMP。

求next数组值的程序如下所示：

vector<int> getNext(string needle)
    {
        int n = needle.size();
        vector<int> next(n + 1); // +1 防止越界
        next[0] = -1; // 第一个匹配不成功指针j返回初始位置
        int post_idx = 0; // 后缀字符串指针
        int pre_idx = -1; // 匹配上的前缀字符串指针
        // 移动后缀指针
        while(post_idx < n)
        {
            // 判断与前缀的重合
            // 从头匹配的时候或当前位置匹配成功就记录
            if (pre_idx == -1 || needle[pre_idx] == needle[post_idx])
            {
                // 注意首先post_idx++，因为下一个位置的next是当前位置的KMP值
                // pre_idx++ 是因为KMP值不是从0计数，前后缀子集重合长度是从1计算
                pre_idx++; post_idx++; 
                next[post_idx] = pre_idx;
            }
            else
            {
                // 若当前位置未匹配上，就可以进入KMP匹配返回
                // 注意这里相当于递归了KMP的使用
                pre_idx = next[pre_idx];
            }
        }
        return next;
    }

参考

https://www.zhihu.com/question/21923021/answer/281346746

https://leetcode.cn/problems/find-the-index-of-the-first-occurrence-in-a-string/solutions/575568/shua-chuan-lc-shuang-bai-po-su-jie-fa-km-tb86/