文章目录
- 1 引言
- 2 学习动机
- 3 经典问题
- 4 解决方案
- 4.1 忽略不确定性
- 4.2 随机规划
- 4.3 鲁棒优化
- 4.4 分布鲁棒优化
- 5 总结
- 相关阅读
1 引言
按2024的原定计划,今年开始要学习不确定优化了。
粗略翻阅了一些相关的书籍和教程,大都包含许多数学公式,瑟瑟发抖。出于只希望学会使用相关技术的初心,我并不想陷入过多的推导和证明过程中,所以至今断断续续持续了两周多,依然不知道该从哪里入门。
思考了一下,系列第一篇还是先阐述自己学习不确定优化的动机,然后梳理针对不确定优化问题的已有解决方案,从而有利于后续设计体系化的学习路径。
正文见下。
2 学习动机
根本上,我要学习不确定优化,是因为在工作中碰到了相关需求。
先描述我遇到的实际业务问题:问题本身可以建模为如下的0-1整数规划
max
f
(
x
)
=
c
T
x
s.t
A
x
=
b
x
∈
{
0
,
1
}
\max \quad f(\pmb x)=\pmb c^T\pmb x \\ \text{s.t} \quad \pmb A\pmb x=\pmb b \\ \pmb x \in \{0,1\}
maxf(x)=cTxs.tAx=bx∈{0,1}
优化变量是千量级,未来至多是几十万量级;目标函数中的
c
\pmb c
c是模型预测出来的值,所以其值可能是不准确的;约束中的
A
\pmb A
A虽然有波动,但从业务判断,该值可以简化是常量,
b
\pmb b
b是常量。
如果将 c \pmb c c当做常量,那这个问题是很容易求解的。但是直接优化得到的最优解,无法保证其落地使用后的核心指标也是最优的。
此前就已经踩过一个坑:在另一个项目中,直接当做常量求解后的落地核心指标甚至不如已有人工策略的落地核心指标好。
为了防止重蹈覆辙,领导希望我在给出最优决策方案时,能充分考虑预测不准带来的影响。
事实上,不仅这个项目遇到了这个问题,其他很多项目也有类似的需求。为了能解决好此类问题,我才决定今年深入学习一下不确定优化相关内容。
针对不确定优化,我比较关注的点有两个:
(1)考虑参数的不确定性后,核心指标能提升多少? 这个问题可以从已公开的行业案例中寻找答案。但遗憾的是,虽然很多学术文章中涉及了不确定优化的正向效果,但是行业应用的实际案例却少之又少。从一些非公开渠道得知,在库存优化场景中,不确定优化方法确实是有落地应用的,核心指标大概能提升几个点。
(2)如何考虑参数的不确定性,对应的解决方案是什么? 这方面的公开内容已经有很多了,主流的解决方案包括:随机规划、鲁棒优化和分布鲁棒优化。作为系列第一篇,本文并不打算精确地描述清楚这些解决方案,而是想通过一个实例的求解,直观地展示不同解决方案的具体思路。
3 经典问题
既然要用实例,自然要使用不确定优化领域中的最经典问题——报童问题。
报童每天需要采购一定数量的报纸用于当天的销售。已知每份报纸的成本价 c = 5 c=5 c=5,销售价 p = 10 p=10 p=10,需求量 d d d是个不确定的变量,通过历史的经验得到其平均值是15,如果当天卖不完,会按回收价 r r r将未卖完的报纸返卖给回收站,为了后续计算方便,本文假设 r = 0 r=0 r=0。
现在需要确定报童的最佳订购量 q q q,使得报童的净收入 θ \theta θ最大化。
4 解决方案
4.1 忽略不确定性
最简单的解决方案是忽略其不确定性,即 d = 15 d=15 d=15。
此时,最佳订购量显然是
q
=
d
=
15
q=d=15
q=d=15
对应的净收入为
θ
=
15
∗
(
10
−
5
)
=
75
\theta= 15 * (10 - 5) = 75
θ=15∗(10−5)=75
4.2 随机规划
本节开始,我们考虑 d d d的不确定性。随机规划模型中,认为 d d d的分布函数已知,举个例子: d d d可以取10,12,18,20,对应的概率分别为 1 6 , 1 3 , 1 3 , 1 6 \frac{1}{6},\frac{1}{3},\frac{1}{3},\frac{1}{6} 61,31,31,61。
随机规划模型的核心思路是:优化
q
q
q使得
θ
\theta
θ的期望值最大化。 此时,目标函数变为
E
(
θ
)
=
1
6
p
min
(
q
,
10
)
+
1
3
p
min
(
q
,
12
)
+
1
3
p
min
(
q
,
18
)
+
1
6
p
min
(
q
,
20
)
−
c
q
\text{E}(\theta) = \frac{1}{6}p\min(q, 10) + \frac{1}{3}p\min(q, 12) + \frac{1}{3}p\min(q, 18) + \frac{1}{6}p\min(q, 20) -cq
E(θ)=61pmin(q,10)+31pmin(q,12)+31pmin(q,18)+61pmin(q,20)−cq
E
(
θ
)
\text{E}(\theta)
E(θ)随
q
q
q的变化曲线如下图所示。显然,当
q
∈
[
12
,
18
]
q\in[12,18]
q∈[12,18]时,期望收益
E
(
θ
)
\text{E}(\theta)
E(θ)取到最大,为56.67。
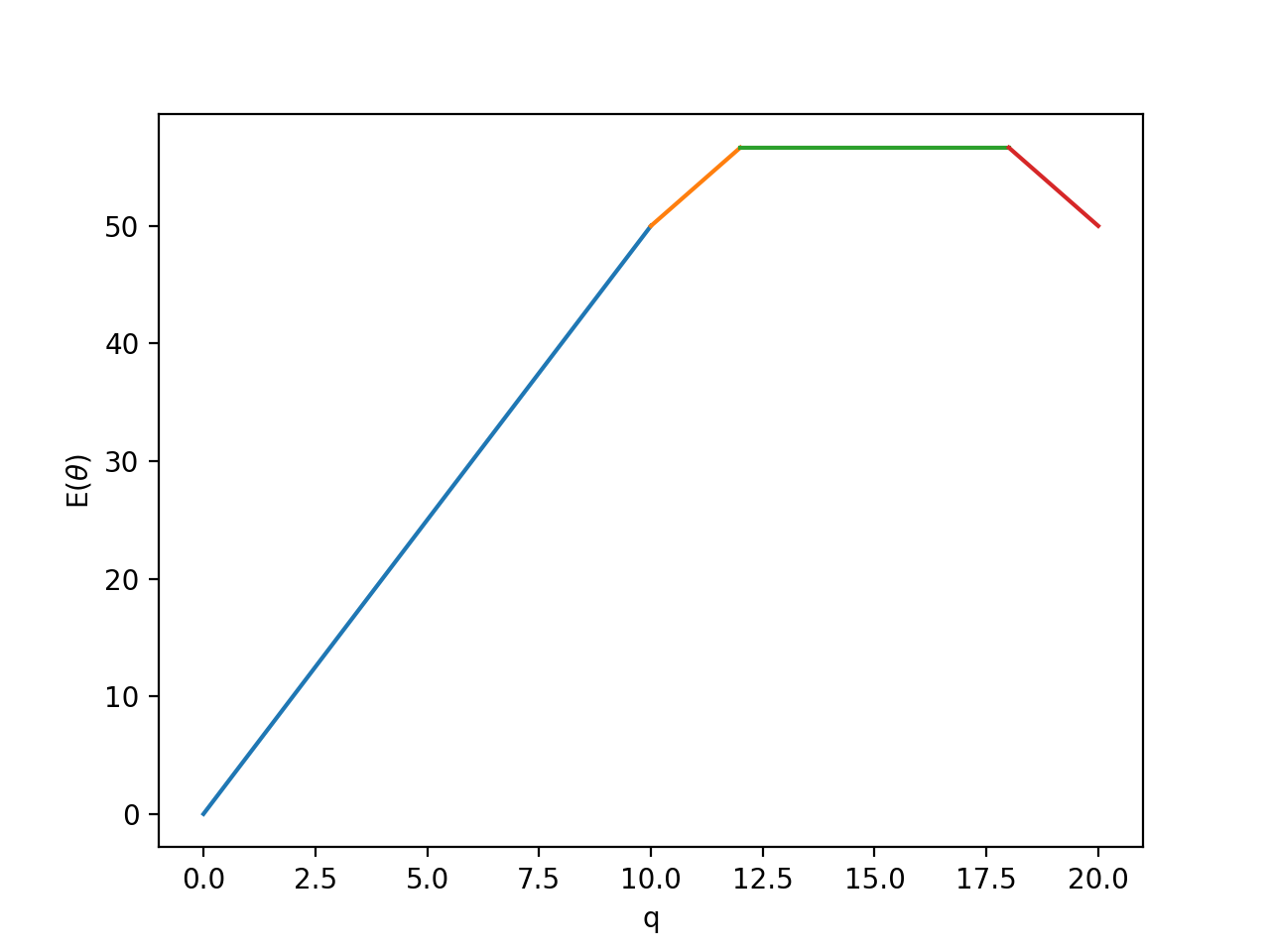
这里需要注意的是,此时的最优解为期望值,而不是实际收益。
4.3 鲁棒优化
在鲁棒优化模型中,一般认为 d d d的分布函数未知,但是其分布的基本信息是已知的,举个例子: d ∈ [ 10 , 20 ] d\in[10, 20] d∈[10,20]。显然,随机规划中的实例可以理解为本节实例的一种特殊情况。但由于分布函数未知,所以无法使用随机规划的方式来求解。
鲁棒优化的核心思路是:寻找
d
d
d为最差情况下的最优解。 数学化的表达方式为:
max
q
min
d
{
p
⋅
min
(
q
,
p
)
−
c
q
}
\mathop{\max}_q \mathop{\min}_d \{ p·\min(q, p)-cq\}
maxqmind{p⋅min(q,p)−cq}
首先分析内层
min
d
\mathop{\min}_d
mind。从下图可以看出,针对同一个
q
q
q,
d
d
d越大,
θ
=
p
⋅
min
(
q
,
p
)
−
c
q
\theta=p·\min(q, p)-cq
θ=p⋅min(q,p)−cq越大,所以最差情况下,
d
=
10
d=10
d=10。
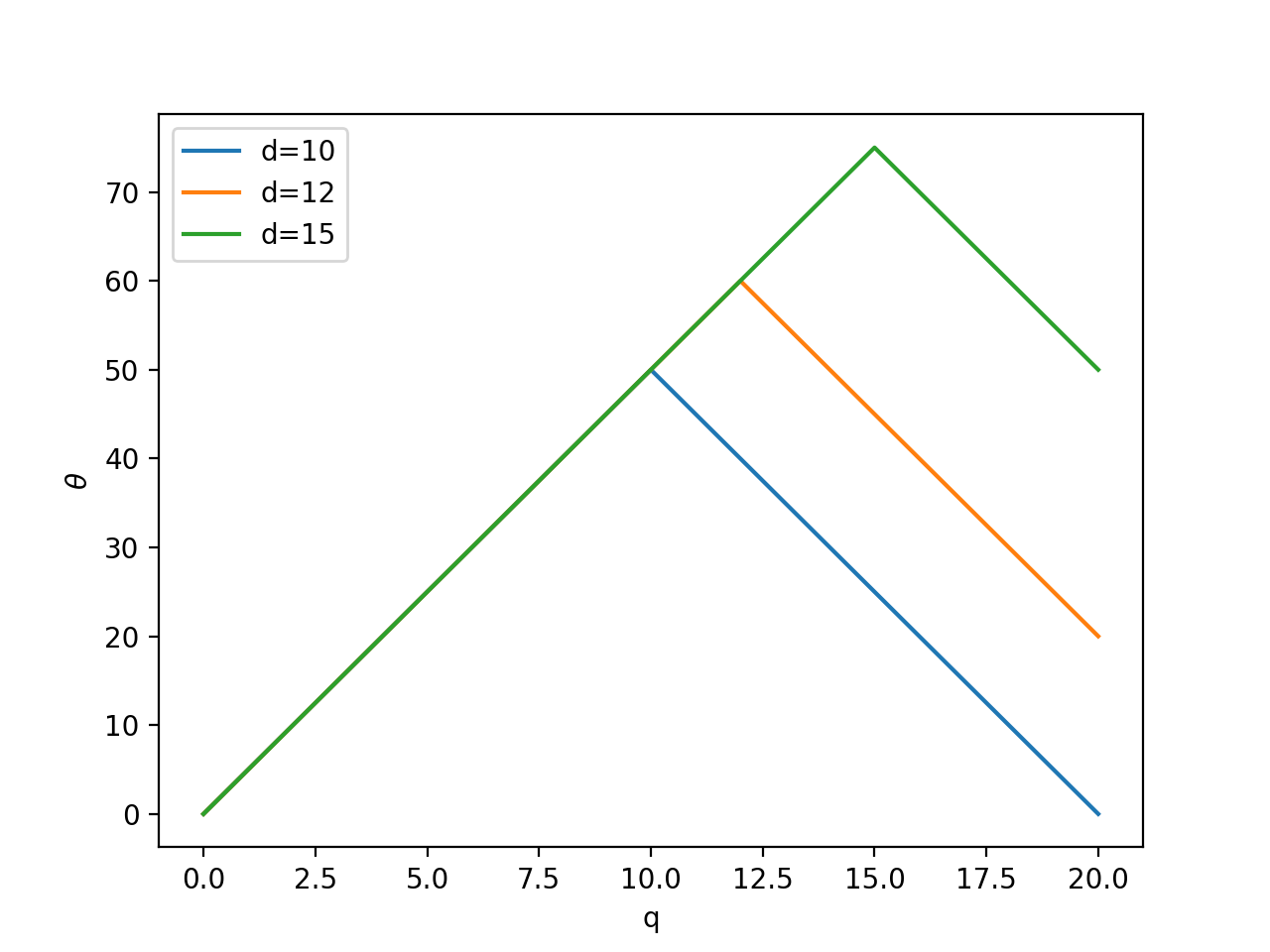
然后分析外层
max
q
\mathop{\max}_q
maxq。从图上也很容易看出,最佳订购量
q
=
10
q=10
q=10,此时
θ
=
50
\theta=50
θ=50。
4.4 分布鲁棒优化
对比随机规划和鲁棒优化,我们可以发现,从针对 d d d的不确定性刻画来看,随机规划是非常精确的,就是某个确定的分布函数;而鲁棒优化则非常模糊,得到的解也是非常保守的。
为了能在两者之间做折中,分布鲁棒优化应运而生:一方面增加不确定参数的分布特征,另一方面追求不那么保守的解。
举个例子,我们不仅知道 d ∈ [ 10 , 20 ] d\in[10, 20] d∈[10,20],我们还知道, d d d的概率值会随其值的增大先增大后减小。那么此时,至少能想到的一些可能的分布情况有:
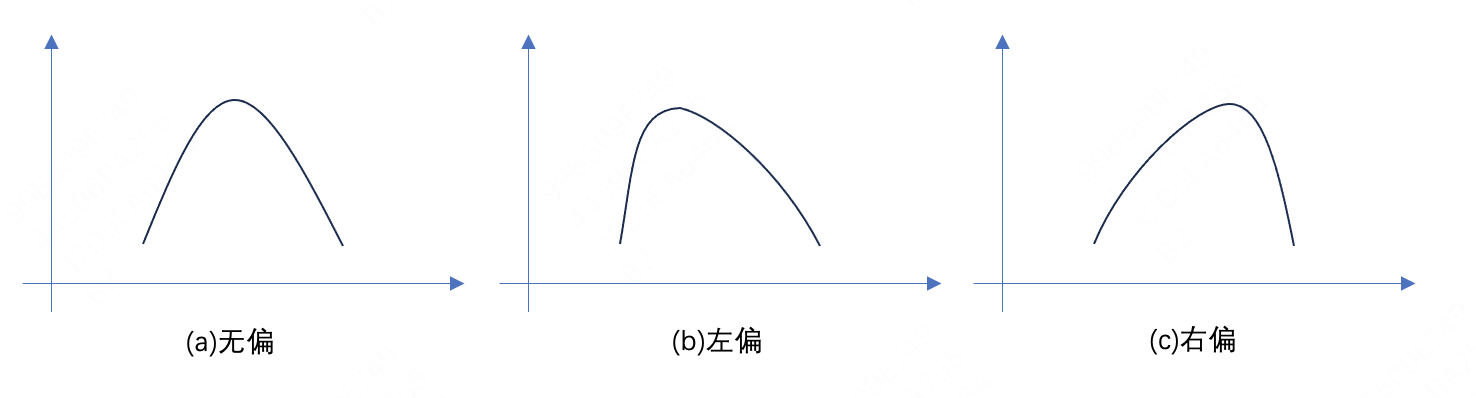
分布鲁棒优化的解决方案是:寻找满足不确定参数特征的最差分布函数,然后以此分布函数为基准,使用随机规划的思路得到最优解。
为了让实例构造简单一些,我们假设分布就以上三种情况,并且对应的分布函数分别只有一种:
(1)无偏: d d d取10,12,18,20的概率分别为 1 6 , 1 3 , 1 3 , 1 6 \frac{1}{6},\frac{1}{3},\frac{1}{3},\frac{1}{6} 61,31,31,61。该情况下,随机规划一节中已经计算过,最优期望收益为56.67。
(2)左偏: d d d取10,12,18,20的概率分别为 37 216 , 72 216 , 67 216 , 40 216 \frac{37}{216},\frac{72}{216},\frac{67}{216},\frac{40}{216} 21637,21672,21667,21640。该情况下的最优订购量是12,最优期望收益是56.57。
(3)右偏: d d d取10,12,18,20的概率分别为 22 108 , 31 108 , 36 108 , 19 108 \frac{22}{108},\frac{31}{108},\frac{36}{108},\frac{19}{108} 10822,10831,10836,10819。该情况下的最优订购量是18,对应的期望收益为56.48。
所以,最差分布函数为右偏,此时最佳的期望收益为56.48。
5 总结
至此,针对每一种解决方案的思路描述和实例讲解算是结束了,看起来并没有那么复杂。
本节我们再横向对比一下这些解决方案,以探查他们之间的联系和区别,加深对它们的认知:
(1)鲁棒优化中认为,不确定参数的分布函数是未知的,仅知道其分布的简单信息;分布鲁棒优化中认为,虽然分布函数未知,但是分布的一些特征是已知的;随机规划则认为分布函数是完全已知的。所以从针对不确定参数的刻画来看,其确定性是逐渐增加的。
(2)鲁棒优化最终求解得到的是一个具体的解,而分布鲁棒优化和随机规划最终得到的是一个期望值。
(3)分布鲁棒优化一方面借鉴了鲁棒优化中的考虑最差情况的思路,另一方面又借鉴了随机规划中求期望的思路,所以看起来最有前景。
(4)从解的质量来看,忽略不确定性的最优解≥随机规划解≥分布鲁棒优化解≥鲁棒优化解。
忽略不确定性的解和考虑不确定性的解之间的差异,可以理解为不确定性约束带来的指标损失。
相关阅读
分布鲁棒优化入门视频:https://www.bilibili.com/video/BV19a411s7cy/?spm_id_from=333.880.my_history.page.click&vd_source=f416a5e7c4817e8efccf51f2c8a2c704






![[ESP32 IDF] wifi 的应用](https://img-blog.csdnimg.cn/direct/c34225b0eea04112a2f97e188d02273a.png)

