【数据结构和算法】--- 二叉树（5）--二叉树OJ题

一、二叉树OJ题

1.1 单值二叉树

题目描述： 如果二叉树每个节点都具有相同的值，那么该二叉树就是单值二叉树。只有给定的树是单值二叉树时，才返回true；否则返回 false。

做题链接： 965. 单值二叉树

解题思路：
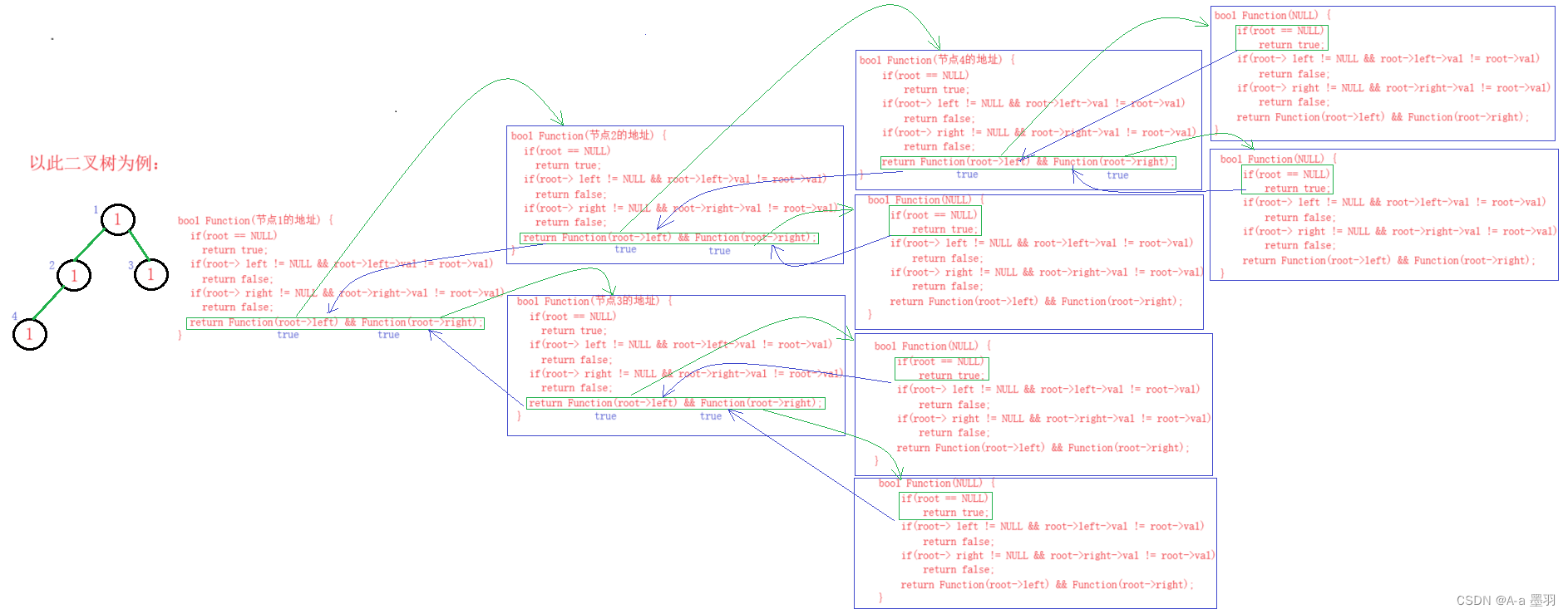
我们可以利用递归分治的思想，将此问题分解为：根节点和左孩子的值是否相等(root->left->val != root->val)，根节点和右孩子的值是否相等(root->right->val != root->val)，左子树判断，右子树判断。
且在每次值相等判断之前都要 先确定，当前根节点是否为空(root == NULL)，若为空就直接返回true表示相等。因为我们会不能确定当前节点的左右孩子是否为空节点，所以每次在比较当前节点和孩子节点的值的时候，都要先判断(root->left != NULL或root->right != NULL)，以确保不会对空节点解引用。如果值不相等便返回false。
最后一步便是继续递归当前节点的左子树(root->left)和右子树(root->right)，那么如果左子树或右子树都为相同的值那么便返回true，如果有一个不相同便会返回false。既然这样，那么我们便可使用&&将递归左和右子树的函数连接起来(isUnivalTree(root->left) && isUnivalTree(root->right))。并将此结果作为返回值，只有同为true，才会真正的返回true。

解题代码：

bool isUnivalTree(struct TreeNode* root) {
    if(root == NULL)
        return true;
    //左右孩子和当前节点的值的判断
    //1、先判孩子不为空； 2、再判孩子和根的值。
    if(root-> left != NULL && root->left->val != root->val)
        return false;
    if(root-> right != NULL && root->right->val != root->val)
        return false;
    //左右子树的递归判断
    return isUnivalTree(root->left) && isUnivalTree(root->right);
}

代码图解：
在这里插入图片描述

1.2 检查两颗树是否相同

题目描述： 给你两棵二叉树的根节点p和 q，编写一个函数来检验这两棵树是否相同。如果两个树在结构上相同，并且节点具有相同的值，则认为它们是相同的。

做题链接： 100. 相同的树

解题思路：
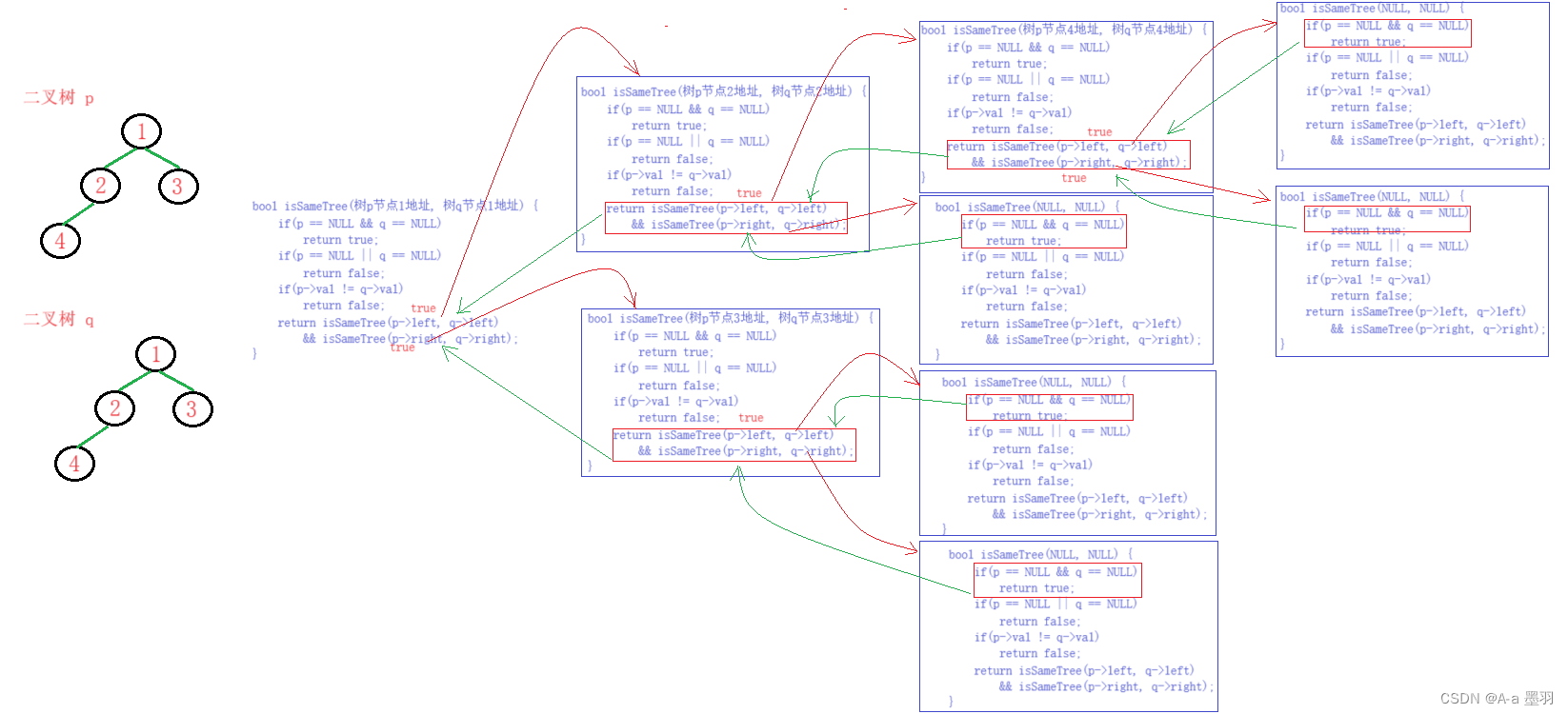
同样可以利用递归分治的思想：两棵二叉树根节点是否相同，左子树是否相同，右子树是否相同。 首先判断两棵二叉树的根节点是否为空，若都为空(p == NULL && q == NULL)则定为相等，返回true。但是如果只有一个节点是空节点的话，那么便要返回false，此处可以使用p == NULL || q == NULL来判断。
相信有人会问，这样判断的话如果两个都是空节点的话，那不就返回false了吗？当然不会，如果能从第一个判断出来，就说明不会出现都为空的情况，那么进入此if语句的条件就只有两个节点中的一个为空！
判断完空节点的情况，我们便可判断这两个节点的值是否相同，若不同则返回false。最后再递归两棵二叉树的左右子树，若两函数都为true，则最终返回true。

解题代码：

bool isSameTree(struct TreeNode* p, struct TreeNode* q) {
    if(p == NULL && q == NULL)
        return true;
    if(p == NULL || q == NULL)
        return false;
    if(p->val != q->val)
        return false;
    return isSameTree(p->left, q->left) && isSameTree(p->right, q->right);
}

代码图解：
在这里插入图片描述

1.3 对称二叉树

题目描述： 给你一个二叉树的根节点 root ，检查它是否轴对称。

做题链接： 101. 对称二叉树

解题思路：
在这里插入图片描述
看上面这个二叉树，如果我们将它分为，根节点，左子树，右子树。如果将左子树和右子树拆分开，那么判断对称二叉树，便可转化为检查两颗树是否相同！！
那么便可在1.2的基础上修改一下代码即可，即二叉树p的左子树和二叉树q的右子树是否相同，(isSameTree(p->left, q->right) && isSameTree(p->right, q->left))，因为两棵二叉树是镜像的关系。

解题代码：

//检查两颗树是否相同
bool isSameTree(struct TreeNode* p, struct TreeNode* q)
{
    if(!p && !q)
        return true;
    if(!p || !q)
        return false;
    if(q->val != p->val)
        return false;
    return isSameTree(p->left, q->right) && isSameTree(p->right, q->left);
}
//分出左右子树
bool isSymmetric(struct TreeNode* root) {
    return isSameTree(root->left, root->right);
}

1.4 另一颗树的子树

题目描述： 给你两棵二叉树 root和 subRoot 。检验 root 中是否包含和 subRoot具有相同结构和节点值的子树。如果存在，返回true ；否则，返回false。
二叉树 tree的一棵子树包括 tree 的某个节点和这个节点的所有后代节点。tree也可以看做它自身的一棵子树。

做题链接： 572. 另一棵树的子树

解题思路：
此题思路任然与1.2检查两颗树是否相同，相似。若在root中寻找subRoot，那么便可以先判断当前二叉树root与sunRoot是否相似，若相似则返回true；不相似则继续递归root的左子树和右子树。 还需要注意的是，此处判断左右子树的函数使用||相连，因为只要左右子树中一个有subRoot即可。

解题代码：

bool isSubtree(struct TreeNode* root, struct TreeNode* subRoot){
    if(root == NULL && subRoot == NULL)
        return true;
    if(root == NULL || subRoot == NULL)
        return false;
    if(root->val != subRoot->val)
        return false;
    return isSubtree(root->left,subRoot) || isSubtree(root->right,subRoot);
}

1.5 平衡二叉树

做题链接： 110. 平衡二叉树

题目描述： 给定一个二叉树，判断它是否是高度平衡的二叉树。本题中，一棵高度平衡二叉树定义为：一个二叉树每个节点的左右两个子树的高度差的绝对值不超过 1 。

解题思路：
既然要判断左右子树的高度差，那么就要写出求二叉树的高度的函数。此函数实现思想：遇到空节点便返回0，然后递归左右子树，每递归一层便加一，返回左子树高度和右子树高度中的较大者，利用fmax()函数求较大值，具体思想还请参考图解：
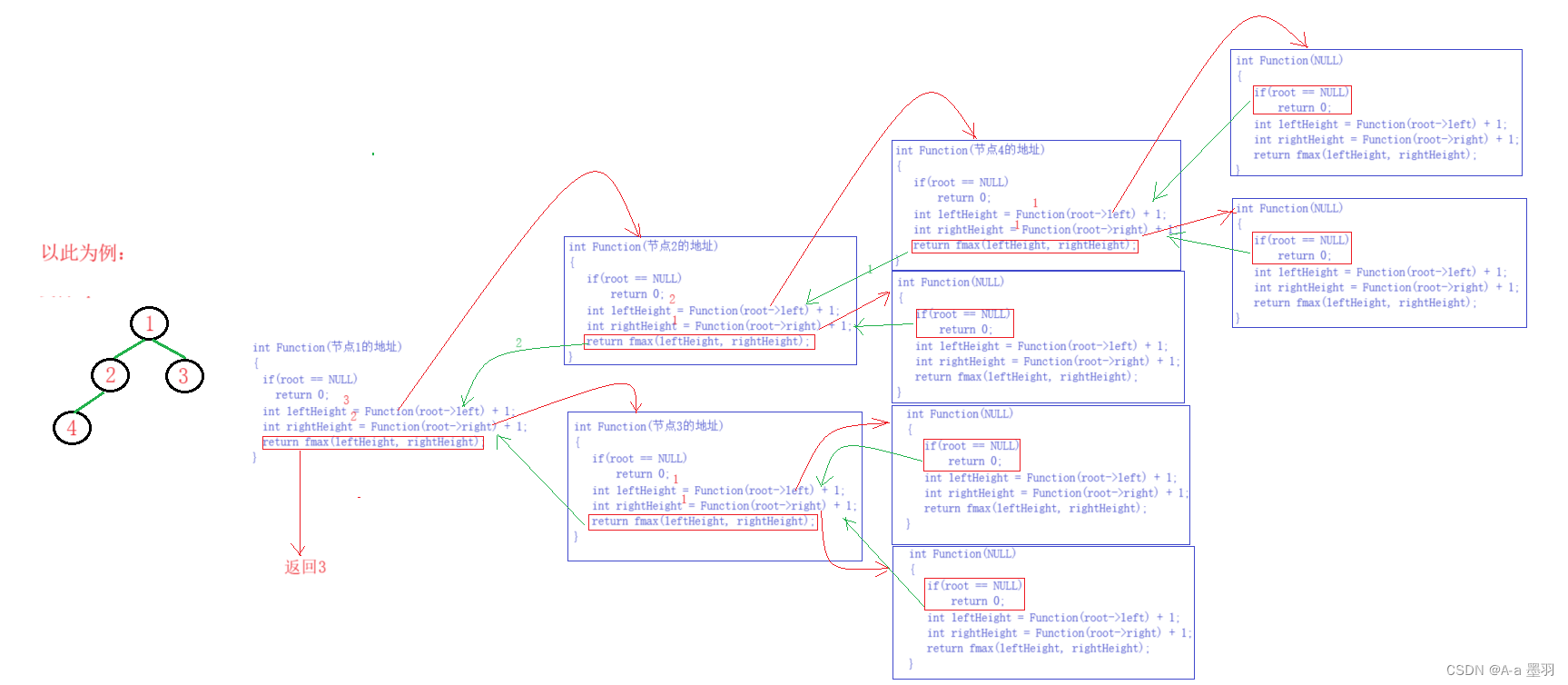
在这里插入图片描述
基于上述求二叉树最大高度的函数BinaryTreeHeight，那么便可利用递归分治的思想：根节点下左右子树的高度差，根节点左孩子作为二叉树第一层的左右子树的高度差，根节点右孩子作为二叉树第一层的左右子树的高度差。
遇到空节点便返回true，先利用BinaryTreeHeight函数求出左子树(leftHeight)和右子树(rightHeight)的最大高度，然后比较高度差(abs(leftHeight - rightHeight) > 1)，若大于一则返回false，最后再递归左右子树。

解题代码：

//求当前节点下的左子树和右子树高度，并返回较大值
int BinaryTreeHeight(struct TreeNode* root)
{
   if(root == NULL)
       return 0;
   int leftHeight = BinaryTreeHeight(root->left) + 1;
   int rightHeight = BinaryTreeHeight(root->right) + 1;
   return fmax(leftHeight, rightHeight);
}
//主函数
bool isBalanced(struct TreeNode* root) 
{
    if(root == NULL)
        return true;
    //左 右子树高度
    int leftHeight = BinaryTreeHeight(root->left);
    int rightHeight = BinaryTreeHeight(root->right);
    //差值判断
    if(abs(leftHeight - rightHeight) > 1)
        return false;
    //递归左右子树
    return isBalanced(root->left) && isBalanced(root->right);
}

二、概念选择题

在一颗完全二叉树中，某一个结点没有其左孩子，则该结点一定（B）
A.是根结点
B.是叶结点
C.是分支结点
D.在倒数第二层

解析： 完全二叉树中如果一个节点没有左孩子，则一定没有右孩子，必定为一个叶子节点，最后一层一定为叶子节点，但是倒数第二层也可能存在叶子节点。

有n个元素的完全二叉树的深度是（D）
A.nlogn
B.nlogn+1
C.logn
D.logn+1
在一颗度为3的树中，度为3的结点有2个，度为2的结点有1个，度为1的结点有2个，则叶子结点有（B）个。

解析： 设度为i的节点个数为ni。该树总共有n个节点，则n=n0+n1+n2+n3。有n个节点的树的总边数为n-1条。根据度的定义，总边数与度之间的关系为：n-1=0*n0+1*n1+2*n2+3*n3。联立两个方程求解，可以得到n0 = n2 + 2n3 + 1, n0=6。

下列关于二叉树的叙述错误的是（ A）
A.二叉树指的是深度为 2 的树
B.一个 n 个结点的二叉树将拥有 n-1 条边
C.一颗深度为 h 的满二叉树拥有 2^h-1 个结点（根结点深度为1）
D.二叉树有二叉链和三叉链两种表示方式

解析： A错误：二叉树指最大孩子个数为2，即树的度为二的树。深度描述的为树的层数。
B正确：对于任意的树都满足：边的条数比节点个数少1，因为每个节点都有双亲，但是根节点没有
C正确：正确，参加二叉树性质
D正确：二叉链一般指孩子表示法，三叉连指孩子双亲表示法，这两种方式是二叉树最常见的表示方式，虽然还有孩子兄弟表示法，该中表示方式本质也是二叉链。

设根结点的深度为1，则一个拥有n个结点的二叉树的深度一定在（A）区间内
A.[log(n + 1)，n]
B.[logn，n]
C.[log(n + 1)，n - 1]
D.[log(n + 1)，n + 1]

解析： 最大深度：即每次只有一个节点，次数二叉树的高度为n，为最高的高度。最小深度：此树为完全二叉树，如果是完全二叉树。根据二叉树性质，完全二叉树的高低为 h = log(n+1)向上取整。