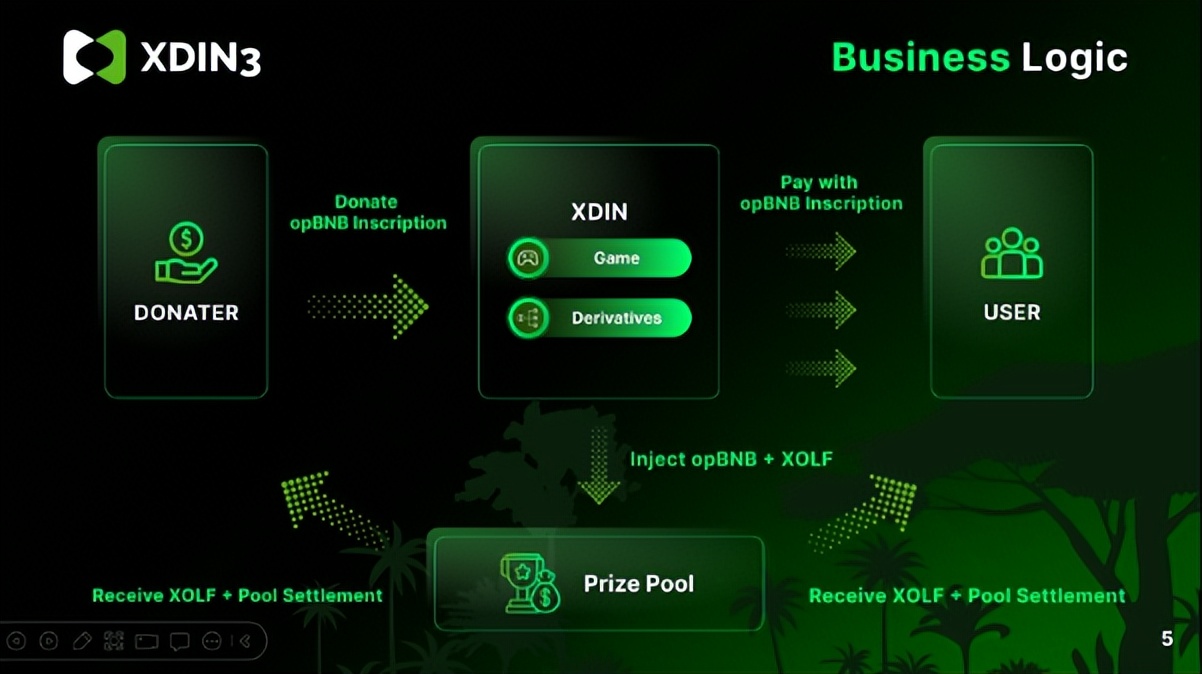
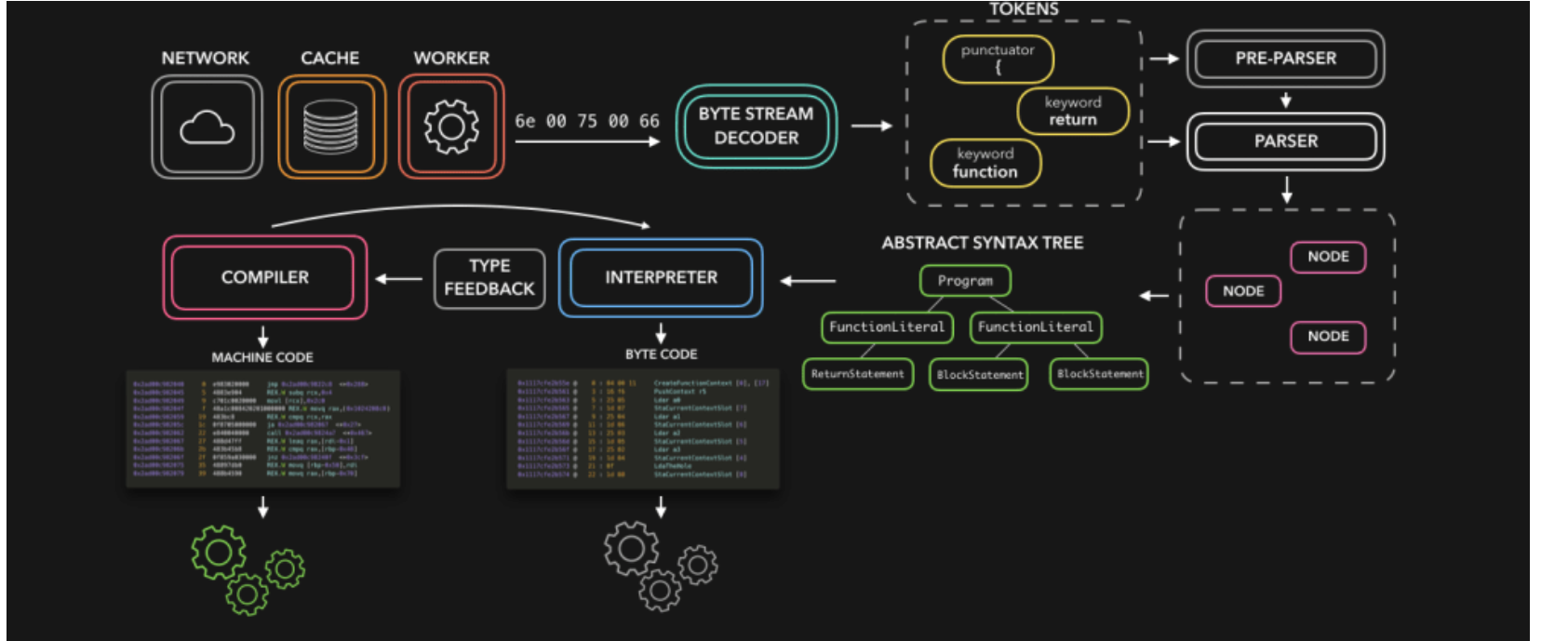
报名明年4月蓝桥杯软件赛的同学们,如果你是大一零基础,目前懵懂中,不知该怎么办,可以看看本博客系列:备赛20周合集
20周的完整安排请点击:20周计划
每周发1个博客,共20周。
在QQ群上交流答疑:

文章目录
- 1. Floyd算法
- 2. Bellman-ford算法
- 3. Dijkstra算法
- 4. 练习题
第19周: 最短路
最短路问题是最广为人知的图论问题,也是蓝桥考核最多的图论问题。
在“第十四周 BFS”中提到BFS也是一种很不错的最短路算法。不过它只适合一种场景:任意的相邻两点之间距离相等,一般把这个距离看成1,称为“1跳”,从起点到终点的路径长度就是多少个“跳数”。在这种场景下,查找一个起点到一个终点的最短距离,BFS是最优的最短路径算法,计算复杂度是O(n),n是图上点的数量。
在更多的应用场景中,需要用不同的算法来解决, 有这些通用的最短路径算法:Floyd、Dijkstra、Bellman-ford、SPFA算法。
Floyd算法是最简单的最短路径算法,代码仅有4行且非常易懂。它的效率不高,不能用于大图,但是在某些场景下也有自己的优势,难以替代。Floyd算法是一种“多源”最短路算法,一次计算能得到图中每一对结点之间(多对多)的最短路径。
Bellman-Ford、Dijkstra、SPFA算法都是“单源”最短路径算法,一次计算能得到一个起点到其他所有点(一对多)的最短路径。
蓝桥杯以前经常考最短路,考过Floyd、BFS、Bellman-Ford、Dijkstra,不过这2年没怎么出题,是不是因为以前考多了,累了。例如2023年省赛的几十道题中只考了一题最短路,用到Dijkstra。
下面介绍Floyd、Bellman-Ford、Dijkstra。Floyd、Bellman-Ford都非常简单,代码短,存图的数据结构简单。Dijkstra难一些,初学者可能比较费劲。
1. Floyd算法
求图上两点i、j之间的最短距离,可以按“从小图到全图”的步骤,在逐步扩大图的过程中计算和更新最短路,这是动态规划的思路。定义状态为dp[k][i][j],i、j、k是点的编号,范围1 ~ n。状态dp[k][i][j]表示在包含1 ~ k点的子图上,点对i、j之间的最短路。当从子图1 ~ k-1扩展到子图1 ~ k时,状态转移方程这样设计:
dp[k][i][j] = min(dp[k-1][i][j], dp[k-1][i][k] + dp[k-1][k][j])
计算过程如下图所示,虚线圆圈内是包含了1 ~ k-1点的子图。方程中的dp[k-1][i][j]是虚线子图内的点对i、j的最短路;dp[k-1][i][k] + dp[k-1][k][j]是经过k点的新路径的长度,即这条路径从i出发,先到k,再从k到终点j。比较不经过k的最短路径dp[k-1][i][j]和经过k的新路径,较小者就是新的dp[k][i][j]。每次扩展一个新点k时,都能用到1 ~ k-1的结果,从而提高了效率。这就是动态规划的方法。
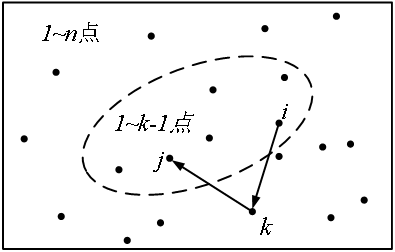
图1 从子图1~k-1扩展到1~k
当k从1逐步扩展到n时,最后得到的dp[n][i][j]是点对i、j之间的最短路径长度。由于i和j是图中所有的点对,所以能得到所有点对之间的最短路。
初值dp[0][i][j],若i、j是直连的,就是它们的边长;若不直连,赋值为无穷大。
由于i、j是任意点对,所以计算结束后得到了所有点对之间的最短路。
下面是代码,仅有4行。这里把dp[][][]缩小成了dp[][],用到了滚动数组,因为dp[k][][]只和dp[k-1][][]有关,所以可以省掉k这一维。由于k是动态规划的子问题的“阶段”,即k是从点1开始逐步扩大到n的,所以k循环必须放在i、j循环的外面。三重循环,复杂度
O
(
n
3
)
O(n^3)
O(n3)。
for(int k=1; k<=n; k++) //floyd的三重循环
for(int i=1; i<=n; i++)
for(int j=1; j<=n; j++) // k循环在i、j循环外面
dp[i][j] = min(dp[i][j], dp[i][k] + dp[k][j]); //比较:不经过k、经过k
Floyd算法的寻路极为盲目,几乎“毫无章法”,这是它的效率低于其他算法的原因。但是,这种“毫无章法”,在某些情况下却有优势。
与其他最短路径算法相比,Floyd有以下特点。
(1)能在一次计算后求得所有结点之间的最短距离,其他最短路径算法都做不到。
(2)代码极其简单,是最简单的最短路算法。三重循环结束后,所有点对之间的最短路都得到了。
(3)效率低下,计算复杂度是
O
(
n
3
)
O(n^3)
O(n3),只能用于n < 300的小规模的图。
(4)存图用邻接矩阵dp[][]是最好最合理的,不用更省空间的邻接表。因为Floyd算法计算的结果是所有点对之间的最短路,本身就需要
n
2
n^2
n2的空间,用矩阵存储最合适。
(5)能判断负圈。负圈是什么?若图中有权值为负的边,某个经过这个负边的环路,所有边长相加的总长度也是负数,这就是负圈。在这个负圈上每绕一圈,总长度就更小,从而陷入在负圈上兜圈子的死循环。Floyd算法很容易判断负圈,只要在算法运行过程出现任意一个dp[i][i] < 0就说明有负圈。因为dp[i][i]是从i出发,经过其他中转点绕一圈回到自己的最短路径,如果小于零,就存在负圈。
下面的场景适用Floyd算法。
(1)图的规模小,点数n < 400。计算复杂度
O
(
n
3
)
O(n^3)
O(n3)限制了图的规模。这种小图不需要用其他算法,其他算法的代码长,写起来麻烦。
(2)问题的解决和中转点有关。这是Floyd算法的核心思想,算法用DP方法遍历中转点来计算最短路。
(3)路径在“兜圈子”,一个点可能多次经过。这是Floyd算法的特长,其他路径算法都不行。
(4)允许多次询问不同点对之间的最短路。这是Floyd算法的优势。
蓝桥公园
【题目描述】小明来到了蓝桥公园。已知公园有N个景点,景点和景点之间一共有M条道路。小明有Q个观景计划,每个计划包含一个起点st 和一个终点ed,表示他想从st去到ed。但是小明的体力有限,对于每个计划他想走最少的路完成,你可以帮帮他吗?
【输入描述】输入第一行包含三个正整数 N,M,Q。第2到M+1行每行包含三个正整数u,v,w,表示 u、v之间存在一条距离为w的路。第M+2到M+Q−1行每行包含两个正整数st,ed,其含义如题所述。
1≤N≤400,1≤M≤N×(N−1)/2,Q≤103,1≤u,v,st,ed≤n,1≤w≤109
【输出描述】输出共Q行,对应输入数据中的查询。若无法从st到达ed则输出−1。
这一题简单演示了Floyd算法的基本应用。边数1 ≤ M ≤ N×(N−1)/2,说明是一个稠密图。当M = N×(N−1)/2时,任意两个点之间都有边。
代码很简单,但是也有一些坑点,请仔细看注释。
c++代码
#include <bits/stdc++.h>
using namespace std;
const long long INF = 0x3f3f3f3f3f3f3f3fLL; //这样定义INF的好处是: INF <= INF+x
const int N = 405;
long long dp[N][N];
int n,m,q;
void input(){
// for(int i = 1; i <= n; i++)
// for(int j = 1; j <= n; j++) dp[i][j] = INF;
memset(dp,0x3f,sizeof(dp)); //初始化,和上面2行功能一样
for(int i = 1; i <= m; i++){
int u,v;long long w;
cin >> u >> v >> w;
dp[u][v]=dp[v][u] = min(dp[u][v] , w); //防止有重边
}
}
void floyd(){
for(int k = 1; k <= n; k++)
for(int i = 1; i <= n; i++)
for(int j = 1; j <= n; j++)
dp[i][j] = min(dp[i][j] , dp[i][k] + dp[k][j]);
}
void output(){
while(q--){
int s, t; cin >> s >>t;
if(dp[s][t]==INF) cout << "-1" <<endl;
else if(s==t) cout << "0" <<endl; //如果不这样,dp[i][i]不等于0
else cout <<dp[s][t]<<endl;
}
}
int main(){
cin >> n>> m >> q;
input(); floyd(); output();
return 0;
}
java代码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static final long INF = 0x3f3f3f3f3f3f3f3fL;
static final int N = 405;
static long[][] dp = new long[N][N];
static int n, m, q;
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
m = sc.nextInt();
q = sc.nextInt();
input(sc);
floyd();
output(sc);
}
static void input(Scanner sc) {
for (int i = 1; i <= n; i++) Arrays.fill(dp[i], INF);
for (int i = 1; i <= m; i++) {
int u = sc.nextInt();
int v = sc.nextInt();
long w = sc.nextLong();
dp[u][v] = dp[v][u] = Math.min(dp[u][v], w);
}
}
static void floyd() {
for (int k = 1; k <= n; k++)
for (int i = 1; i <= n; i++)
for (int j = 1; j <= n; j++)
dp[i][j] = Math.min(dp[i][j], dp[i][k] + dp[k][j]);
}
static void output(Scanner scanner) {
while (q-- > 0) {
int s = scanner.nextInt();
int t = scanner.nextInt();
if (dp[s][t] == INF) System.out.println("-1");
else if (s == t) System.out.println("0");
else System.out.println(dp[s][t]);
}
}
}
Python代码
n,m,q=map(int,input().split())
dp = [[int(0x3f3f3f3f3f3f3f3f) for _ in range(405)]for _ in range(405)]
def input_():
global dp
for i in range(1,m+1):
u,v,w = map(int,input().split())
ww = min(dp[u][v],w) #去掉重边
dp[u][v] = ww
dp[v][u] = ww
def floyd():
global dp
for k in range(1, n + 1):
for i in range(1, n + 1):
for j in range(1, n + 1):
if dp[i][k]+dp[k][j]<dp[i][j]: dp[i][j] = dp[i][k]+dp[k][j]
def output():
global q
for i in range(q):
s,t = map(int,input().split())
if dp[s][t] == 0x3f3f3f3f3f3f3f3f: print(-1)
elif s==t: print(0)
else: print(dp[s][t])
input_()
floyd()
output()
2. Bellman-ford算法
Bellman-ford算法是单源最短路径算法,它的原理十分简单易懂:一个有n个点的图,给每个点n次机会询问邻居,是否有到起点s的更短的路径,如果有就更新;经过n轮更新,就得到了所有点到起点s的最短路。
第1轮:起点s的邻居点中,肯定有一个点u是最近的;第1轮确定了s到u的最短路。
第2轮:所有点再次询问邻居,是否有到s的更短的路;显然,要么是s的某个邻居,要么是u的某个邻居,能确定最短路。
重复以上步骤,每一轮能确定一个点的最短路。n个点共n轮计算,每一轮需要检查所有的m条边,总复杂度O(m×n)。Bellman-ford算法能用于边权为负数的图,这是它对Dijkstra算法的优势,基于“扩散+贪心”的Dijkstra算法,边的权值不能为负。
Bellman-Ford算法的特点是只对相邻结点进行计算,可以避免floyd那种大撒网式的无效计算,大大提高了效率。为理解这个算法,可以想象图上的每个点都站着一个人,初始时,所有人到s的距离设为INF,即无限大。用下面的步骤求最短路径:
(1)第一轮,给所有的n个人每人一次机会,问他的邻居,到s的最短距离是多少?如果他的邻居到s的距离不是INF,他就能借道这个邻居到s去,并且把自己原来的INF更新为较短的距离。显然,开始的时候,起点s的直连邻居(例如u)肯定能更新距离,而u的邻居(例如v),如果在u更新之后问u,那么v有机会更新,否则就只能保持INF不变。特别地,在第一轮更新中,存在一个与s最近的邻居t;t到s的直连距离,就是全图中t到s的最短距离。因为它通过别的邻居绕路到s,肯定更远。t的最短距离已经得到,后面不会再更新。
(2)第二轮,重复第一轮的操作,再给每个人一次问邻居的机会。这一轮操作之后,至少存在一个s或t的邻居v,可以算出它到s的最短距离。v要么与s直连,要么是通过t到达s的。v的最短距离也得到了,后面不会再更新。
(3)第三轮,再给每个人一次机会…
继续以上操作,直到所有人都不能再更新最短距离为止。
一共需要几轮操作?每一轮操作,都至少有一个新的结点得到了到s的最短路径。所以,最多只需要n轮操作,就能完成n个结点。在每一轮操作中,需要检查所有m个边,更新最短距离。根据以上分析,Bellman-Ford算法的复杂度是O(nm)。
Bellman-Ford有现实的模型,即问路。每个十字路口站着一个警察;在某个路口,路人问一个警察,怎么走到s最近?如果这个警察不知道,他会问相邻几个路口的警察:“从你这个路口走,能到s吗?有多远?”这些警察可能也不知道,他们会继续问新的邻居。这样传递下去,最后肯定有个警察是s路口的警察,他会把s的信息返回给他的邻居,邻居再返回给邻居。最后所有的警察都知道怎么走到s。而且是最短的路。
问路模型里有趣的一点,并且能体现Bellman-Ford思想的是:警察并不需要知道到s的完整的路径,他只需要知道从自己的路口出发,往哪个方向走能到达s,并且路最近。
2022第十三届国赛 出差
【题目描述】A国有N个城市,编号为1 . . . N。小明是编号为1的城市中一家公司的员工,今天突然接到了上级通知需要去编号为N的城市出差。由于疫情原因,很多直达的交通方式暂时关闭,小明无法乘坐飞机直接从城市1到达城市N,需要通过其他城市进行陆路交通中转。小明通过交通信息网,查询到了M条城市之间仍然还开通的路线信息以及每一条路线需要花费的时间。同样由于疫情原因,小明到达一个城市后需要隔离观察一段时间才能离开该城市前往其他城市。通过网络,小明也查询到了各个城市的隔离信息。(由于小明之前在城市1,因此可以直接离开城市1,不需要隔离)由于上级要求,小明希望能够尽快赶到城市N,因此他求助于你,希望你能帮他规划一条路线,能够在最短时间内到达城市N。
【输入】第1行:两个正整数N, M, N表示A国的城市数量,M表示未关闭的路线数量。第2行:N个正整数,第i个整数Ci表示到达编号为i的城市后需要隔离的时间。第3 . . . M + 2行:每行3个正整数,u, v, c,表示有一条城市u到城市v的双向路线仍然开通着,通过该路线的时间为c。
【输出】第1行:1个正整数,表示小明从城市1出发到达城市N的最短时间(到达城市N,不需要计算城市N的隔离时间)。
对于100%的数据,1≤N≤1000 , 1≤M≤10000, 1≤Ci≤200, 1≤u, v≤N, 1≤c≤1000
本题是求最短路径,数据规模1≤N≤1000 , 1≤M≤10000不算大。用那种算法?用复杂度
O
(
n
3
)
O(n^3)
O(n3)的floyd算法超时;用复杂度O(mn)的Bellman-ford算法正好;没有必要使用更好的Dijkstra和SPFA算法。
两点之间的边长,除了路线时间c,还要加上隔离时间。经过这个转化后,本题是一道简单的Bellman-ford算法模板题。
(1)C++代码
第7行用struct edge{int a,b,c;}来存边。这种简单的存储方法,不能快速搜索点和边,不过正适合Bellman-ford这种简单的算法。本题的边是无向边,要存为双向边,见13-14行。
Bellman-ford算法的代码相当简单,几乎和Floyd的代码一样短。
#include<bits/stdc++.h>
using namespace std;
const int INF = 0x3f3f3f3f;
const int M = 20010; //双向边的最大数量
int t[M];
int dist[M]; //dist[i]: 起点到第i点的最短路
struct edge{int a,b,c;}e[M]; //分开操作也行:int a[M],b[M],c[M];
int main(){
int n,m; cin>>n>>m;
for(int i=1;i<=n;i++) cin>>t[i];
for(int i=1;i<=m;i++){
int a,b,c; cin >>a>>b>>c;
e[i].a=a; e[i].b=b; e[i].c=c; //双向边,a->b
e[m+i].a=b; e[m+i].b=a; e[m+i].c=c; //双向边: b->a
}
//下面是bellman-ford
memset(dist,INF,sizeof(dist)); //初始化为无穷大
dist[1]=0; //起点是1,1到自己距离为0
for(int k=1;k<=n;k++){ //一共有n轮操作
for(int i=1;i<=2*m;i++){ //检查每条边
int u=e[i].a,v=e[i].b; //u的一个邻居是v
int res = t[v]; //隔离时间
if(v==n) res = 0; //终点不用隔离
dist[v]=min(dist[v],dist[u]+e[i].c+res); //u通过v到起点的距离更短,更新
}
}
cout<<dist[n];
return 0;
}
java代码
import java.util.Arrays;
import java.util.Scanner;
public class Main {
static final int INF = 0x3f3f3f3f;
static final int M = 20010;
static int[] t = new int[M];
static int[] dist = new int[M];
static Edge[] e = new Edge[M];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
for (int i = 1; i <= n; i++) t[i] = sc.nextInt();
for (int i = 1; i <= m; i++) {
int a = sc.nextInt();
int b = sc.nextInt();
int c = sc.nextInt();
e[i] = new Edge(a, b, c);
e[m + i] = new Edge(b, a, c);
}
bellmanFord(n, m);
System.out.println(dist[n]);
}
static void bellmanFord(int n, int m) {
Arrays.fill(dist, INF);
dist[1] = 0;
for (int k = 1; k <= n; k++) {
for (int i = 1; i <= 2 * m; i++) {
int u = e[i].a;
int v = e[i].b;
int res = t[v];
if (v == n) res = 0;
dist[v] = Math.min(dist[v], dist[u] + e[i].c + res);
}
}
}
static class Edge {
int a;
int b;
int c;
public Edge(int a, int b, int c) {
this.a = a; this.b = b; this.c = c;
}
}
}
python代码
下面的代码原样改写了上面的C++代码。也用简单的数组存边。由于Python很慢,这份代码的复杂度虽然和上面C++代码一样,但是运行时间特别长,判题系统需要加到10倍时间。
n, m = map(int, input().split())
t= [0]+[int(i) for i in input().split()] #不用t[0],从t[1]开始
e = [] #简单的数组存点和边
for i in range(1,m+1):
a, b,c = map(int, input().split())
e.append([a,b,c])
e.append([b,a,c]) #双向边
dist=[0x3f3f3f3f]*(n+1)
dist[1]=0
for k in range(1,n+1):
for a,b,c in e: #检查每条边
res=t[b]
if b==n: res=0
dist[b]=min(dist[b],dist[a]+c+res)
print(dist[n])
3. Dijkstra算法
Dijkstra算法是最有名的最短路径算法,也是一般性的最短路径问题中最常用、效率最高的。与Floyd这种“多源”最短路径算法不同,Dijkstra是一种“单源”最短路径算法,一次计算能得到从一个起点s到其他所有点的最短距离长度,并能记录到每个点的最短路径上的途径点。
1. 算法思想
Dijkstra的模型用多米诺骨牌做例子,读者可以想象下面的场景。
在图中所有的边上,排满多米诺骨牌,相当于把骨牌看成图的边。一条边上的多米诺骨牌数量,和边的权值(例如长度或费用)成正比。规定所有骨牌倒下的速度都是一样的。如果在一个结点上推倒骨牌,会导致这个结点上的所有骨牌都往后面倒下去。
在起点s推倒骨牌,可以观察到,从s开始,它连接的边上的骨牌都逐渐倒下,并到达所有能达到的结点。在某个结点t,可能先后从不同的线路倒骨牌过来;先倒过来的骨牌,其经过的路径,肯定就是从s到达t的最短路;后倒过来的骨牌,对确定结点t的最短路没有贡献,不用管它。
从整体看,这就是一个从起点s扩散到整个图的过程。
在这个过程中,观察所有结点的最短路径是这样得到的:
(1)在s的所有直连邻居中,最近的邻居u,骨牌首先到达。u是第一个确定最短路径的结点。从u直连到s的路径肯定是最短的,因为如果u绕道别的结点到s,必然更远。
(2)然后,把后面骨牌的倒下分成2部分,一部分是从s继续倒下到s的其它的直连邻居,另一部分从u出发倒下到u的直连邻居。那么下一个到达的结点v,必然是s或者u的一个直连邻居。v是第二个确定最短路径的结点。
(3)继续以上步骤,在每一次迭代过程中,都能确定一个结点的最短路径。
Dijkstra算法应用了贪心法的思想,即“抄近路走,肯定能找到最短路径”。算法可以简单概况为:Dijkstra = BFS + 贪心。实际上,“Dijkstra + 优先队列 = BFS + 优先队列(队列中的数据是从起点到当前点的距离)”。
下面分析复杂度。设图的点有n个,边有m条。编码的时候,集合A一般用优先队列来模拟。优先队列可以用堆或其他高效的数据结构实现,往优先队列中插入一个数、取出最小值的操作都是O(logn)的。一共往队列中插入m次(每条边都要进集合A一次),取出n次(每次从集合A中取出距离s最短的一个点,取出时要更新这个点的所有邻居到s的距离,设一个点平均有k个邻居),那么总复杂度是O(m×logn + n×k×logn) O(m×logn),一般有m大于n。
2. 编程实现
代码的主要内容是维护两个集合:已确定最短路径的结点集合A、这些结点向外扩散的邻居结点集合B。步骤是:
(1)把起点s放到A中,把s所有的邻居放到B中。此时,邻居到s的距离就是直连距离。
(2)从B中找出距离起点s最短的结点u,放到A中。
(3)把u所有的新邻居放到B中。显然,u的每一条边都连接了一个邻居,每个新邻居都要加进去。其中u的一个新邻居v,它到s的距离dis(s, v)等于dis(s, u) + dis(u, v)。
(4)重复(2)、(3),直到B为空时,结束。
计算结束后,可以得到从起点s到其它所有点的最短距离。
用下面的例题给出模板代码,其中有2个关键。
用邻接表存图和查找邻居。对邻居的查找和扩展,通过动态数组vector e[N]实现的邻接表。其中e[i]存储第i个结点上所有的边,边的一头是它的邻居,即struct edge的参数to。需要扩展结点i的邻居的时候,查找e[i]即可。已经放到集合A中的结点,不要扩展;用bool done[N]记录集合A,当done[i] = true时,表示它在集合A中,已经找到了最短路。
在集合B中找距离起点最短的结点。直接用STL的优先队列实现,priority_queue <s_node> Q。但是有关丢弃的动作,STL的优先队列无法做到。例如步骤(3)中,需要在B={(2-5), (2-4), (4,7)}中丢弃(2-5),但是STL没有这种操作。在代码中也用bool done[NUM]协助解决这个问题。从优先队列pop出(2-4)时,记录done[2] = true,表示结点2已经处理好。下次从优先队列pop出(2-5)时,判断done[2]是true,丢弃。
蓝桥王国
【题目描述】蓝桥王国一共有N个建筑和M条单向道路,每条道路都连接着两个建筑,每个建筑都有自己编号,分别为1∼。(其中皇宫的编号为1)国王想让小明回答从皇宫到每个建筑的最短路径是多少,但紧张的小明此时已经无法思考,请你编写程序帮助小明回答国王的考核。
【输入描述】输入第一行包含2个正整数N,M。第2到M+1行每行包含三个正整数u,v,w,表示u→v之间存在一条距离为w的路。1≤N≤3×105,1≤m≤106,1≤ui ,vi≤N,0≤wi≤109。
【输出描述】输出仅一行,共N个数,分别表示从皇宫到编号为1∼N建筑的最短距离,两两之间用空格隔开。(如果无法到达则输出−1)
(1)C++代码
下面是基本Dijkstra算法的代码,使用了“邻接表 + 优先队列”。代码的详细内容已经在前面解释。
#include<bits/stdc++.h>
using namespace std;
const long long INF = 0x3f3f3f3f3f3f3f3fLL; //这样定义INF的好处是: INF <= INF+x
const int N= 3e5+2;
struct edge{
int from, to; long long w; //起点,终点,权值。起点from并没有用到,e[i]的i就是from
edge(int a, int b,long long c){from=a; to=b; w=c;}
};
vector<edge>e[N]; //用于存储图
struct s_node{
int id; long long n_dis; //id:结点;n_dis:这个结点到起点的距离
s_node(int b,long long c){id=b; n_dis=c;}
bool operator < (const s_node & a) const
{ return n_dis > a.n_dis;}
};
int n,m;
long long dis[N]; //记录所有结点到起点的距离
void dijkstra(){
int s = 1; //起点s是1
bool done[N]; //done[i]=true表示到结点i的最短路径已经找到
for (int i=1;i<=n;i++) {dis[i]=INF; done[i]=false; } //初始化
dis[s]=0; //起点到自己的距离是0
priority_queue <s_node> Q; //优先队列,存结点信息
Q.push(s_node(s, dis[s])); //起点进队列
while (!Q.empty()) {
s_node u = Q.top(); //pop出距起点s距离最小的结点u
Q.pop();
if(done[u.id]) continue; //丢弃已经找到最短路径的结点。即集合A中的结点
done[u.id]= true;
for (int i=0; i<e[u.id].size(); i++) { //检查结点u的所有邻居
edge y = e[u.id][i]; //u.id的第i个邻居是y.to
if(done[y.to]) continue; //丢弃已经找到最短路径的邻居结点
if (dis[y.to] > y.w + u.n_dis) {
dis[y.to] = y.w + u.n_dis;
Q.push(s_node(y.to, dis[y.to])); //扩展新的邻居,放到优先队列中
}
}
}
}
int main(){
scanf("%d%d",&n,&m);
for (int i=1;i<=n;i++) e[i].clear();
while (m--) {
int u,v,w; scanf("%d%d%lld",&u,&v,&w);
e[u].push_back(edge(u,v,w));
// e[v].push_back(edge(v,u,w)); //本题是单向道路
}
dijkstra();
for(int i=1;i<=n;i++){
if(dis[i]>=INF) cout<<"-1 ";
else printf("%lld ", dis[i]);
}
}
java代码
import java.util.*;
public class Main {
static final long INF = 0x3f3f3f3f3f3f3f3fL;
static final int N = 300002;
static class Edge {
int from;
int to;
long w;
public Edge(int from, int to, long w) {
this.from = from;
this.to = to;
this.w = w;
}
}
static class SNode implements Comparable<SNode> {
int id;
long n_dis;
public SNode(int id, long n_dis) {
this.id = id;
this.n_dis = n_dis;
}
@Override
public int compareTo(SNode o) {
return Long.compare(n_dis, o.n_dis);
}
}
static List<Edge>[] e = new List[N];
static long[] dis = new long[N];
public static void main(String[] args) {
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
int m = sc.nextInt();
for (int i = 1; i <= n; i++) e[i] = new ArrayList<>();
while (m-- > 0) {
int u = sc.nextInt();
int v = sc.nextInt();
long w = sc.nextLong();
e[u].add(new Edge(u, v, w));
}
dijkstra(n);
for (int i = 1; i <= n; i++) {
if (dis[i] >= INF) System.out.print("-1 ");
else System.out.printf("%d ", dis[i]);
}
}
static void dijkstra(int n) {
int s = 1;
boolean[] done = new boolean[N];
Arrays.fill(dis, INF);
dis[s] = 0;
PriorityQueue<SNode> queue = new PriorityQueue<>();
queue.offer(new SNode(s, dis[s]));
while (!queue.isEmpty()) {
SNode u = queue.poll();
if (done[u.id]) continue;
done[u.id] = true;
for (Edge edge : e[u.id]) {
if (done[edge.to]) continue;
if (dis[edge.to] > edge.w + u.n_dis) {
dis[edge.to] = edge.w + u.n_dis;
queue.offer(new SNode(edge.to, dis[edge.to]));
}
}
}
}
}
Python代码
用堆heapq实现优先队列。另外注意邻接表的用法,24行读取u的邻居v和边长w,12行遍历u的邻居v和边长w。
import array, heapq
def dij(s):
done = [0 for i in range(n + 1)]
hp = []
dis[s] = 0
heapq.heappush(hp, (0, s))
while hp:
u = heapq.heappop(hp)[1]
if done[u]: continue
done[u] = 1
for i in range(len(G[u])):
v, w = G[u][i] #遍历u的邻居v,边长w
if done[v]: continue
if dis[v] > dis[u] + w:
dis[v] = dis[u] + w
heapq.heappush(hp, (dis[v], v))
n, m = map(int, input().split())
s = 1
G = [[] for i in range(n+1)] #邻接表存图
INF = 1<<64
dis=[INF]*(n+1)
for i in range(m):
u, v, w = map(int, input().split())
G[u].append((v,w)) #存图,u的一个邻居是v,边长w
dij(s)
for i in range(1, n + 1):
if dis[i]>=INF: print("-1",end=' ')
else: print(dis[i], end=' ')
4. 练习题
洛谷的最短路题目,按难度排序:
https://www.luogu.com.cn/problem/list?tag=160&orderBy=difficulty&order=asc&page=1