深度强化学习(DRL)
本文是学习笔记,如有侵权,请联系删除。本文在ChatGPT辅助下完成。
参考链接
Deep Reinforcement Learning官方链接:https://github.com/wangshusen/DRL
源代码链接:https://github.com/DeepRLChinese/DeepRL-Chinese
B站视频:【王树森】深度强化学习(DRL)
豆瓣: 深度强化学习
文章目录
- 深度强化学习(DRL)
- Actor-Critic Method
- 视频
- Value Network and Policy Network
- Train the Neural Networks
- Summary
- 书
- 价值网络
- 算法推导
- 训练流程
- 用目标网络改进训练
- 本章总结
- 后记
Actor-Critic Method
Actor-Critic方法把价值学习和策略学习结合起来。
视频
下面是视频的学习笔记
Value Network and Policy Network
离散状态下状态价值函数可以写成: V π ( s ) = ∑ a π ( a ∣ s ) ⋅ Q π ( s , a ) . V_{\pi}(s)=\sum_{a}\pi(a|s)\cdot Q_{\pi}(s,a). Vπ(s)=∑aπ(a∣s)⋅Qπ(s,a).
但是其中策略函数 π ( a ∣ s ) \pi(a|s) π(a∣s)和动作价值函数 Q π ( s , a ) Q_{\pi}(s,a) Qπ(s,a)都不知道,可以分别用两个神经网络进行近似,这两个神经网络分别称为策略网络和价值网络,在表述形式上里面分别添加了一个 θ \theta θ和 w w w参数,表示的是神经网络的参数。
策略网络控制agent运动,是actor,相当于是运动员;价值网络不控制agent运动,它负责给agent打分,是critic,相当于裁判。

分别看一下这两个神经网络
策略网络actor,它只有一个输入state,输出是所有action的概率分布。
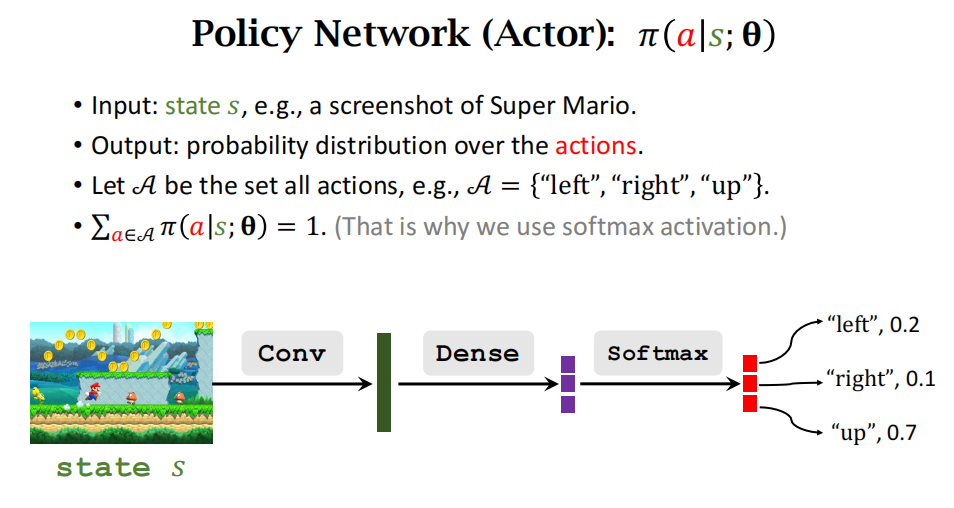
价值网络critic,有两个输入,分别是state和action;输出是一个标量,表示的是对actor的打分。
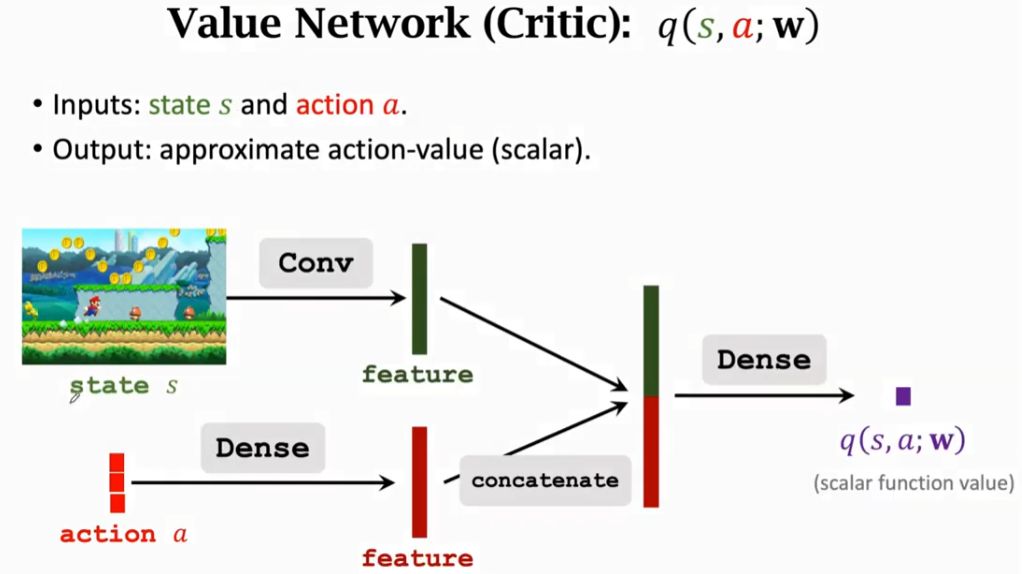
同时学习一个策略和一个值函数就是actor-critic方法。
Train the Neural Networks
训练 π \pi π网络是提高actor的平均分,即让状态价值函数V函数的值更大;让价值网络q来当裁判,给actor的表现打分,更新它的参数 w w w是为了让它的打分越来越精准。通过两个网络,让运动员的得分越来越高,裁判的打分越来越精准。

通过以下五个步骤来对 θ \theta θ和 w w w参数进行更新
- Observe the state s t . s_t. st.
- Randomly sample action α t \color{red}{\alpha_t} αt according to π ( ⋅ ∣ s t ; θ t ) . \pi(\cdot|s_t;\mathbf{\theta}_t). π(⋅∣st;θt).
- Perform a t \color{red}{a_t} at and observe new state s t + 1 s_{t+1} st+1 and reward r t . r_t. rt.
- Update w (in value network) using temporal difference (TD).
- Update θ \mathbf{\theta} θ (in policy network) using policy gradient.

使用时间差分TD算法更新价值网络q,让裁判打分更准
损失函数是预测q和target y t y_t yt之间差的平方

使用策略梯度算法更新策略网络 π \pi π,让运动员得分更高
下图中的V是状态价值函数,相当于运动员所有动作的平均分
策略梯度是状态价值函数V关于 θ \theta θ的导数
定义g是 l o g π log\pi logπ对 θ \theta θ的导数乘以q,这里q是裁判的打分
策略梯度等于对函数g求期望,消掉动作A。
g函数是策略梯度的无偏估计,用g函数代替策略梯度
然后使用随机梯度上升算法来更新 θ \theta θ的值。

ChatGPT:补充梯度的概念
在数学和计算机科学中,梯度是一个向量,表示一个多元函数在某一点上的变化率和变化的方向。对于一个具有多个输入变量的函数,梯度给出了该函数对每个输入变量的偏导数。
考虑一个函数 ( f ( x 1 , x 2 , … , x n ) f(x_1, x_2, \ldots, x_n) f(x1,x2,…,xn)),其梯度记为 ( ∇ f \nabla f ∇f) 或者 ( ∂ f ∂ x \frac{\partial f}{\partial \mathbf{x}} ∂x∂f),其中 ( ∇ \nabla ∇) 是 nabla 符号,表示梯度运算,( x = [ x 1 , x 2 , … , x n ] \mathbf{x} = [x_1, x_2, \ldots, x_n] x=[x1,x2,…,xn]) 是输入变量的向量。梯度是一个向量,其每个分量是函数对相应输入变量的偏导数。
∇ f = [ ∂ f ∂ x 1 , ∂ f ∂ x 2 , … , ∂ f ∂ x n ] \nabla f = \left[ \frac{\partial f}{\partial x_1}, \frac{\partial f}{\partial x_2}, \ldots, \frac{\partial f}{\partial x_n} \right] ∇f=[∂x1∂f,∂x2∂f,…,∂xn∂f]
梯度的方向是函数在某一点上变化最快的方向,而梯度的模(长度)表示变化率。如果梯度的模较大,意味着函数在该点的变化较为剧烈。
在优化问题中,梯度的使用很常见。梯度下降算法就是一种基于梯度的优化方法,通过迭代更新参数,使得目标函数逐渐趋向最小值。梯度上升算法则是类似的优化方法,用于最大化目标函数。
总的来说,梯度是一个重要的数学概念,特别在优化、机器学习和深度学习等领域有广泛的应用。
整个Actor-Critic Method的框图
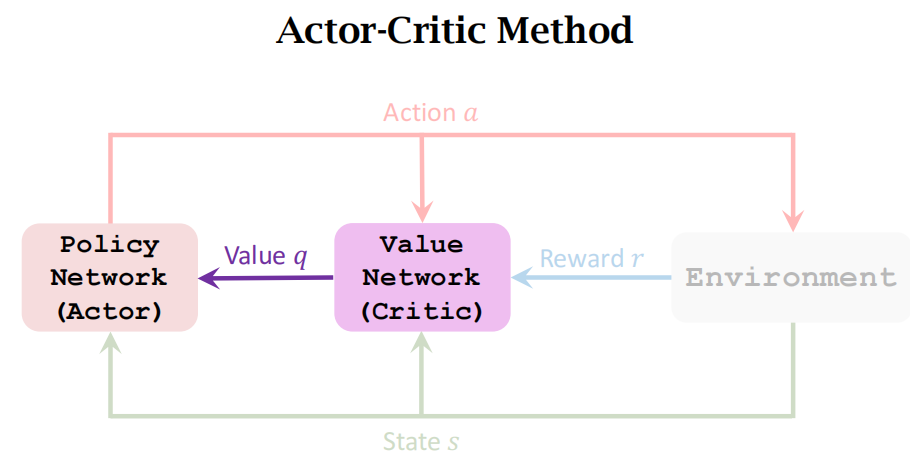
整个算法的流程共有9步,这里是前5步,主要复习以下TD 目标。
r t + γ ⋅ q t + 1 r_t + \gamma \cdot q_{t+1} rt+γ⋅qt+1是TD target,时间差分算法里面的(TD目标表示了在当前时刻 t 的奖励 r t r_t rt 加上未来奖励的折扣。这个目标被用于更新值函数,通过比较当前值函数的估计和这个目标,可以调整值函数的参数以逐渐提高估计的准确性。)

Actor-Critic算法流程:更新价值网络(critic)是梯度下降,更新策略网络(actor)是梯度上升。

上面第9步中用 q t q_t qt更新,也可以用 δ t \delta_t δt来更新。两种方法都是对的。
Summary
总结一下Actor-Critic方法中Actor和 Critic的作用
在训练中,agent是被策略网络控制的,价值网络打分提供反馈;训练后,agent还是被策略网络控制,但此时价值网络(critic)就没用了。

怎样训练两个网络:
策略网络是策略梯度来训练。用梯度上升,让状态价值函数V的值增加,这就意味着运动员的平均分提高。
价值网络是用TD算法来训练。TD算法要用到价值网络的预测 q t q_t qt(价值网络对期望回报的估计)以及TD target(也是对期望回报的估计,由于它用到真实的奖励 r t r_t rt,所以它的估计比 q t q_t qt更靠谱, y t y_t yt作为TD target,相当于监督学习中的标签),对损失函数关于价值网络函数的参数 w w w求导得到梯度,然后用梯度下降,让估计 q t q_t qt更接近TD target 也就是 y t y_t yt。

为什么用损失函数对 w w w求导?ChatGPT的回答:
在机器学习中,使用损失函数对模型参数(例如权重 ( w w w))求导的目的是通过梯度下降或其他优化算法来更新模型参数,以最小化或最大化损失函数。这是因为损失函数衡量了模型在训练数据上的性能,我们的目标是使模型在训练数据上表现得越好越好。
考虑一个典型的机器学习问题,其中我们有输入特征 (X) 和对应的目标变量 ( Y Y Y),我们的模型通过一些参数 (w) 进行参数化,表示为 ( Y = f ( X ; w ) Y = f(X; w) Y=f(X;w))。我们的目标是找到最优的参数 (w),使得模型预测的 (Y) 与真实的目标 (Y) 之间的差距最小。
这个差距通常通过损失函数(也叫目标函数)来定义,表示为 ( L ( Y , f ( X ; w ) ) L(Y, f(X; w)) L(Y,f(X;w)))。梯度下降的思想是沿着损失函数下降最快的方向更新参数,直至找到使损失最小化的参数。
为了更新参数,我们需要计算损失函数关于参数 (w) 的梯度(导数)。梯度是一个向量,其中每个分量表示损失函数关于相应参数的偏导数。通过梯度下降,我们按照梯度的反方向更新参数,使得损失函数逐渐减小。
具体来说,对于参数 (w),我们使用链式法则计算损失函数关于 (w) 的梯度,并使用这个梯度来更新 (w)。这个过程反复进行,直到达到停止条件(例如达到最大迭代次数或梯度变化很小)。
总之,使用损失函数对参数 (w) 求导的目的是优化模型,使其在训练数据上的性能达到最优。
书
策略梯度方法用策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ)更新策略网络参数 θ \theta θ,从而增大目标函数。前面推导出策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 的无偏估计,即下面的随机梯度:
g ( s , a ; θ ) ≜ Q π ( s , a ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boldsymbol{g}(s,a;\boldsymbol{\theta}) \triangleq Q_\pi(s,a) \cdot \nabla_{\boldsymbol{\theta}}\ln\pi(a|s;\boldsymbol{\theta}). g(s,a;θ)≜Qπ(s,a)⋅∇θlnπ(a∣s;θ).
但是其中的动作价值函数 Q π Q_\mathrm{\pi} Qπ 是未知的,导致无法直接计算 g ( s , a ; θ ) g(s,a;\theta) g(s,a;θ)。上一节的 REINFORCE 用实际观测的回报近似 Q π Q_\mathrm{\pi} Qπ, 本节的 actor-critic 方法用神经网络近似 Q π Q_\mathrm{\pi} Qπ 。
价值网络
Actor-critic 方法用一个神经网络近似动作价值函数 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a), 这个神经网络叫做“价值网络”, 记为 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w),其中的 w w w 表示神经网络中可训练的参数。价值网络的输入是状态 s s s, 输出是每个动作的价值。动作空间 A A A 中有多少种动作,那么价值网络的输出就是多少维的向量,向量每个元素对应一个动作。举个例子,动作空间是 A = { 左,右,上 } A= \{ 左,右,上\} A={左,右,上},
q ( s , 左; w ) = 219 , q ( s , 右; w ) = − 73 , q ( s , 上; w ) = 580. \begin{aligned}&q(s,\text{ 左; }\boldsymbol{w})&=&219,\\&q(s,\text{ 右; }\boldsymbol{w})&=&-73,\\&q(s,\text{ 上; }\boldsymbol{w})&=&580.\end{aligned} q(s, 左; w)q(s, 右; w)q(s, 上; w)===219,−73,580.
神经网络的结构见图 7.2。
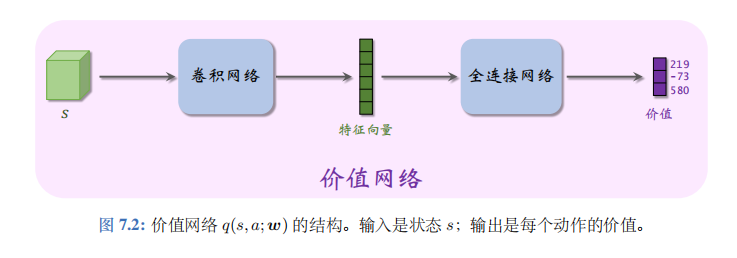
虽然价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w) 与之前学的 DQN 有相同的结构,但是两者的意义不同,训练算法也不同。
- 价值网络是对动作价值函数 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a) 的近似。而 DQN 则是对最优动作价值函数 Q ⋆ ( s , a ) Q_\star(s,a) Q⋆(s,a) 的近似。
- 对价值网络的训练使用的是 SARSA 算法,它属于同策略,不能用经验回放。对 DQN的训练使用的是 Q 学习算法,它属于异策略,可以用经验回放。
算法推导
Actor-critic 翻译成“演员一评委”方法。策略网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 相当于演员,它基于状态 s s s 做出动作 a a a。价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w) 相当于评委,它给演员的表现打分,评价在状态 s s s 的情况下做出动作 a a a的好坏程度。策略网络(演员)和价值网络(评委)的关系如图7.3所示。
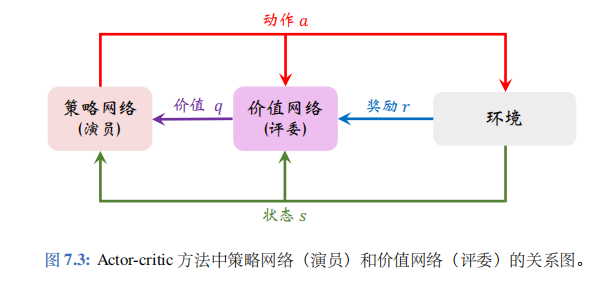
读者可能会对图 7.3 感到不解:为什么不直接把奖励 R R R 反馈给策略网络 (演员),而要用价值网络 (评委) 这样一个中介呢?原因是这样的:策略学习的目标函数 J ( θ ) J(\theta) J(θ) 是回报 U U U 的期望,而不是奖励 R R R 的期望;注意回报 U U U 和奖励 R R R 的区别。虽然能观测到当前的奖励 R R R,但是它对策略网络是毫无意义的;训练策略网络(演员)需要的是回报 U U U,而不是奖励 R R R。价值网络 (评委) 能够估算出回报 U U U 的期望,因此能帮助训练策略网络 (演员)。
训练策略网络 (演员)
策略网络 (演员) 想要改进自己的演技,但是演员自己不知道什么样的表演才算更好,所以需要价值网络(评委) 的帮助。在演员做出动作 a a a 之后, 评委会打一个分数 q ^ ≜ q ( s , a ; w ) \widehat{q}\triangleq q(s,a;\boldsymbol{w}) q ≜q(s,a;w),并把分数反馈给演员,帮助演员做出改进。演员利用当前状态 s s s, 自己的动作 a a a, 以及评委的打分 q ^ \widehat{q} q , 计算近似策略梯度,然后更新自己的参数 θ \theta θ(相当于改变自己的技术)。通过这种方式,演员的表现越来越受评委的好评,于是演员的获得的评分 q ^ \widehat{q} q 越来越高。
训练策略网络的基本想法是用策略梯度 ∇ θ J ( θ ) \nabla_{\theta}J(\theta) ∇θJ(θ) 的近似来更新参数 θ \theta θ。之前我们推导过策略梯度的无偏估计:
g ( s , a ; θ ) ≜ Q π ( s , a ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \boldsymbol{g}(s,a;\boldsymbol{\theta})\:\triangleq\:Q_{\pi}\big(s,a\big)\:\cdot\:\nabla_{\boldsymbol{\theta}}\ln\pi\big(a\:\big|\:s;\:\boldsymbol{\theta}\big). g(s,a;θ)≜Qπ(s,a)⋅∇θlnπ(a s;θ).
价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w) 是对动作价值函数 Q π ( s , a ) Q_{\pi}(s,a) Qπ(s,a) 的近似,所以把上面公式中的 Q π Q_{\pi} Qπ 替换成价值网络,得到近似策略梯度:
g ^ ( s , a ; θ ) ≜ q ( s , a ; w ) ⏟ 评委的打分 ⋅ ∇ θ ln π ( a ∣ s ; θ ) . ( 7.11 ) \begin{array}{rcl}\widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta})&\triangleq&\underbrace{q(s,a;\boldsymbol{w})}_\text{评委的打分}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a\mid s;\boldsymbol{\theta}).\end{array}\quad{(7.11)} g (s,a;θ)≜评委的打分 q(s,a;w)⋅∇θlnπ(a∣s;θ).(7.11)
最后做梯度上升更新策略网络的参数:
θ ← θ + β ⋅ g ^ ( s , a ; θ ) . ( 7.12 ) \theta\leftarrow\theta+\beta\cdot\widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta}).\quad{(7.12)} θ←θ+β⋅g (s,a;θ).(7.12)
注: 用上述方式更新参数之后,会让评委打出的分数越来越高,原因是这样的。状态价值函数 V π ( s ) V_{\pi}(s) Vπ(s) 可以近似成为:
v ( s ; θ ) = E A ∼ π ( ∣ s ; θ ) [ q ( s , A ; w ) ] . v(s;\boldsymbol{\theta})\:=\:\mathbb{E}_{A\sim\pi(\boldsymbol{|}s;\boldsymbol{\theta})}\Big[q(s,A;\boldsymbol{w})\Big]. v(s;θ)=EA∼π(∣s;θ)[q(s,A;w)].
因此可以将 v ( s ; θ ) v(s;\theta) v(s;θ) 看做评委打分的均值。不难证明,公式 (7.11) 中定义的近似策略梯度 g ^ ( s , a ; θ ) \widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta}) g (s,a;θ) 的期望等于 v ( s ; θ ) v(s;\boldsymbol{\theta}) v(s;θ) 关于 θ \theta θ 的梯度:
∇ θ v ( s ; θ ) = E A ∼ π ( ⋅ ∣ s ; θ ) [ g ^ ( s , A ; θ ) ] . \nabla_{\boldsymbol{\theta}v}(s;\boldsymbol{\theta})\:=\:\mathbb{E}_{A\sim\pi(\cdot|s;\boldsymbol{\theta})}\Big[\widehat{\boldsymbol{g}}(s,A;\boldsymbol{\theta})\Big]. ∇θv(s;θ)=EA∼π(⋅∣s;θ)[g (s,A;θ)].
因此,用公式 7.12 中的梯度上升更新 θ \theta θ,会让 v ( s ; θ ) v(s;\theta) v(s;θ) 变大,也就是让评委打分的均值更高。
训练价值网络(评委)
通过以上分析,我们不难发现上述训练策略网络(演员)的方法不是真正让演员表现更好,只是让演员更迎合评委的喜好而已。因此,评委的水平也很重要,只有当评委的打分 q ^ \widehat{q} q 真正反映出动作价值 Q π Q_\pi Qπ,演员的水平才能真正提高。初始的时候,价值网络的参数 w w w 是随机的,也就是说评委的打分是瞎猜。可以用 SARSA 算法更新 w w w,提高评委的水平。每次从环境中观测到一个奖励 r r r,把 r r r 看做是真相,用 r r r 来校准评委的打分。
第 5.1 节已经推导过 SARSA 算法,现在我们再回顾一下。在 t t t 时刻,价值网络输出
q ^ t = q ( s t , a t ; w ) , \widehat q_{t}\:=\:q(s_{t},a_{t};\:\boldsymbol{w}), q t=q(st,at;w),
它是对动作价值函数 Q π ( s t , a t ) Q_\pi(s_t,a_t) Qπ(st,at) 的估计。在 t + 1 t+1 t+1 时刻,实际观测到 r t , s t + 1 , a t + 1 r_t,s_{t+1},a_{t+1} rt,st+1,at+1, 于是可以计算 TD 目标
y t ^ ≜ r t + γ ⋅ q ( s t + 1 , a t + 1 ; w ) , \widehat{y_{t}}\:\triangleq\:r_{t}+\gamma\cdot q\big(s_{t+1},a_{t+1};\:\boldsymbol{w}\big), yt ≜rt+γ⋅q(st+1,at+1;w),
它也是对动作价值函数
Q
π
(
s
t
,
a
t
)
Q_\pi(s_t,a_t)
Qπ(st,at) 的估计。由于
y
^
t
\widehat{y}_t
y
t 部分基于实际观测到的奖励
r
t
r_t
rt,我们认为
y
^
t
\widehat{y}_t
y
t 比
q
(
s
t
,
a
t
;
w
)
q(s_t,a_t;\boldsymbol{w})
q(st,at;w) 更接近事实真相。所以把
y
^
t
\widehat{y}_t
y
t 固定住,鼓励
q
(
s
t
,
a
t
;
w
)
q(s_t,a_t;\boldsymbol{w})
q(st,at;w) 去接近
y
^
t
\widehat{y}_t
y
t。SARSA 算法具体这样更新价值网络参数
w
w
w。定义损失函数:
L
(
w
)
≜
1
2
[
q
(
s
t
,
a
t
;
w
)
−
y
^
t
]
2
.
L(\boldsymbol{w})\triangleq\frac{1}{2}\Big[q\big(s_t,a_t;\boldsymbol{w}\big)-\widehat{y}_t\Big]^2.
L(w)≜21[q(st,at;w)−y
t]2.
设 q ^ t ≜ q ( s t , a t ; w ) \widehat{q}_t\triangleq q(s_t,a_t;\boldsymbol{w}) q t≜q(st,at;w)。损失函数的梯度是:
∇ w L ( w ) = ( q ^ t − y ^ t ) ⏟ TD 误差 δ t ⋅ ∇ w q ( s t , a t ; w ) . \nabla_{\boldsymbol{w}}\:L\big(\boldsymbol{w}\big)\:=\:\underbrace{\big(\widehat{q}_{t}-\widehat{y}_{t}\big)}_{\text{TD 误差 }\delta_{t}}\:\cdot\nabla_{\boldsymbol{w}}\:q\big(s_{t},a_{t};\boldsymbol{w}\big). ∇wL(w)=TD 误差 δt (q t−y t)⋅∇wq(st,at;w).
做一轮梯度下降更新 w : w: w:
w
←
w
−
α
⋅
∇
w
L
(
w
)
.
w\:\leftarrow\:w\:-\:\alpha\cdot\nabla_{\boldsymbol{w}}L(\boldsymbol{w}).
w←w−α⋅∇wL(w).
这样更新
w
w
w 可以让
q
(
s
t
,
a
t
;
w
)
q(s_t,a_t;\boldsymbol{w})
q(st,at;w) 更接近
y
^
t
\widehat{y}_t
y
t。可以这样理解 SARSA: 用观测到的奖励
r
t
r_t
rt 来“校准”评委的打分
q
(
s
t
,
a
t
;
w
)
q(s_t,a_t;\boldsymbol{w})
q(st,at;w)。
训练流程
下面概括 actor-critic 训练流程。设当前策略网络参数是
θ
n
o
w
\theta_\mathrm{now}
θnow,价值网络参数是
w
n
o
w
w_\mathrm{now}
wnow。
执行下面的步骤,将参数更新成
θ
n
e
w
\theta_\mathrm{new}
θnew 和
w
n
e
w
w_\mathrm{new}
wnew:
- 观测到当前状态 s t s_t st,根据策略网络做决策 : a t ∼ π ( ⋅ ∣ s t ; θ n o w ) :a_t\sim\pi(\cdot|s_t;\theta_\mathrm{now}) :at∼π(⋅∣st;θnow), 并让智能体执行动作 a t a_t at。
- 从环境中观测到奖励 r t r_t rt 和新的状态 s t + 1 s_{t+1} st+1。
- 根据策略网络做决策 : a ~ t + 1 ∼ π ( ⋅ ∣ s t + 1 ; θ n o w ) :\tilde{a}_{t+1}\sim\pi(\cdot|s_{t+1};\theta_{\mathrm{now}}) :a~t+1∼π(⋅∣st+1;θnow),但不让智能体执行动作 a ~ t + 1 \tilde{a}_{t+1} a~t+1。
- 让价值网络打分:
q ^ t = q ( s t , a t ; w n o w ) 和 q ^ t + 1 = q ( s t + 1 , a ~ t + 1 ; w n o w ) \widehat q_{t}\:=\:q\big(s_{t},a_{t};\:\boldsymbol{w_{\mathrm{now}}}\big)\quad\text{和}\quad\widehat q_{t+1}\:=\:q\big(s_{t+1},\tilde{a}_{t+1};\:\boldsymbol{w_{\mathrm{now}}}\big) q t=q(st,at;wnow)和q t+1=q(st+1,a~t+1;wnow)
- 计算 TD 目标和 TD 误差:
y ^ t = r t + γ ⋅ q ^ t + 1 和 δ t = q ^ t − y ^ t . \widehat y_{t}\:=\:r_{t}+\gamma\cdot\widehat q_{t+1}\quad\text{和}\quad\delta_{t}\:=\:\widehat q_{t}-\widehat y_{t}. y t=rt+γ⋅q t+1和δt=q t−y t.
- 更新价值网络:
w n e w ← w n o w − α ⋅ δ t ⋅ ∇ w q ( s t , a t ; w n o w ) . w_{\mathrm{new}}\:\leftarrow\:w_{\mathrm{now}}\:-\:\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}q\big(s_{t},a_{t};\:\boldsymbol{w_{\mathrm{now}}}\big). wnew←wnow−α⋅δt⋅∇wq(st,at;wnow).
- 更新策略网络:
θ n e w ← θ n o w + β ⋅ q ^ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) . \theta_{\mathrm{new}}\:\leftarrow\:\theta_{\mathrm{now}}\:+\:\beta\cdot\widehat{q}_{t}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta}_{\mathrm{now}}). θnew←θnow+β⋅q t⋅∇θlnπ(at∣st;θnow).
用目标网络改进训练
第 6.2 节讨论了 Q 学习中的自举及其危害,以及用目标网络 (target network) 缓解自举造成的偏差。SARSA 算法中也存在自举一一即用价值网络自己的估值 q ^ t + 1 \widehat{q}_{t+1} q t+1 去更新价值网络自己;我们同样可以用目标网络计算 TD 目标,从而缓解偏差。把目标网络记作 q ( s , a ; w − ) q(s,a;\boldsymbol{w}^-) q(s,a;w−),它的结构与价值网络相同,但是参数不同。使用目标网络计算 TD 目标,那么 actor-critic 的训练就变成了:
-
观测到当前状态 s t s_t st,根据策略网络做决策 : a t ∼ π ( ⋅ ∣ s t ; θ n o w ) :a_t\sim\pi(\cdot|s_t;\theta_\mathrm{now}) :at∼π(⋅∣st;θnow), 并让智能体执行动作 a t a_t at。
-
从环境中观测到奖励 r t r_t rt 和新的状态 s t + 1 s_{t+1} st+1。
-
根据策略网络做决策 : a ~ t + 1 ∼ π ( ⋅ ∣ s t + 1 ; θ n o w ) :\tilde{a}_{t+1}\sim\pi(\cdot|s_{t+1};\theta_{\mathrm{now}}) :a~t+1∼π(⋅∣st+1;θnow),但是不让智能体执行动作 a ~ t + 1 \tilde{a}_{t+1} a~t+1。
-
让价值网络给 ( s t , a t ) (s_t,a_t) (st,at) 打分:
q ^ t = q ( s t , a t ; w n o w ) . \widehat q_{t}\:=\:q(s_{t},a_{t};\:\boldsymbol{w_{\mathrm{now}}}). q t=q(st,at;wnow).
- 让目标网络给 ( s t + 1 , a ~ t + 1 ) (s_{t+1},\tilde{a}_{t+1}) (st+1,a~t+1) 打分:
q ^ t + 1 − = q ( s t + 1 , a ~ t + 1 ; w n o w ~ ) . \widehat q_{t+1}^{-}\:=\:q\big(s_{t+1},\tilde{a}_{t+1};\:\tilde{w_{\mathrm{now}}}\big). q t+1−=q(st+1,a~t+1;wnow~).
- 计算 TD 目标和 TD 误差:
y ^ t − = r t + γ ⋅ q ^ t + 1 − 和 δ t = q ^ t − y ^ t − . \widehat y_{t}^{-}\:=\:r_{t}+\gamma\cdot\widehat q_{t+1}^{-}\quad\text{和}\quad\delta_{t}\:=\:\widehat q_{t}-\widehat y_{t}^{-}. y t−=rt+γ⋅q t+1−和δt=q t−y t−.
- 更新价值网络:
w n e w ← w n o w − α ⋅ δ t ⋅ ∇ w q ( s t , a t ; w n o w ) . w_{\mathrm{new}}\:\leftarrow\:w_{\mathrm{now}}-\:\alpha\cdot\delta_{t}\cdot\nabla_{\boldsymbol{w}}q\big(s_{t},a_{t};\:\boldsymbol{w}_{\mathrm{now}}\big). wnew←wnow−α⋅δt⋅∇wq(st,at;wnow).
- 更新策略网络:
θ n e w ← θ n o w + β ⋅ q ^ t ⋅ ∇ θ ln π ( a t ∣ s t ; θ n o w ) . \theta_{\mathrm{new}}\:\leftarrow\:\theta_{\mathrm{now}}\:+\:\beta\cdot\widehat{q}_{t}\cdot\nabla_{\boldsymbol{\theta}}\ln\pi(a_{t}\:|\:s_{t};\:\boldsymbol{\theta}_{\mathrm{now}}). θnew←θnow+β⋅q t⋅∇θlnπ(at∣st;θnow).
- 设 τ ∈ ( 0 , 1 ) \tau\in(0,1) τ∈(0,1) 是需要手动调整的超参数。做加权平均更新目标网络的参数:
w n e w − ← τ ⋅ w n e w + ( 1 − τ ) ⋅ w n o w − . w_{\mathrm{new}}^{-}\:\leftarrow\:\tau\cdot w_{\mathrm{new}}\:+\:\left(1-\tau\right)\cdot\boldsymbol{w_{\mathrm{now}}^{-}}. wnew−←τ⋅wnew+(1−τ)⋅wnow−.
本章总结
-
可以用神经网络 π ( a ∣ s ; θ ) \pi(a|s;\theta) π(a∣s;θ) 近似策略函数。策略学习的目标函数是 J ( θ ) = E S [ V π ( S ) ] J(\theta)=\mathbb{E}_S[V_\pi(S)] J(θ)=ES[Vπ(S)], 它的值越大,意味着策略越好。
-
策略梯度指的是 J ( θ ) J(\theta) J(θ) 关于策略参数 θ \theta θ 的梯度。策略梯度定理将策略梯度表示成
g ( s , a ; θ ) ≜ Q π ( s , a ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) \boldsymbol{g}(s,a;\boldsymbol{\theta})\:\triangleq\:Q_{\pi}(s,a)\:\cdot\:\nabla_{\boldsymbol{\theta}}\ln\pi(a\:|\:s;\:\boldsymbol{\theta}) g(s,a;θ)≜Qπ(s,a)⋅∇θlnπ(a∣s;θ)
的期望。
- REINFORCE 算法用实际观测的回报 u u u 近似 Q π ( s , a ) Q_\pi(s,a) Qπ(s,a) , 从而把 g ( s , a ; θ ) g(s,a;\theta) g(s,a;θ) 近似成:
g ~ ( s , a ; θ ) ≜ u ⋅ ∇ θ ln π ( a ∣ s ; θ ) . \tilde{\boldsymbol{g}}(s,a;\boldsymbol{\theta})\triangleq\:u\:\cdot\:\nabla_{\boldsymbol{\theta}}\ln\pi(a\:|\:s;\:\boldsymbol{\theta}). g~(s,a;θ)≜u⋅∇θlnπ(a∣s;θ).
REINFORCE 算法做梯度上升更新策略网络: θ ← θ + β ⋅ g ~ ( s , a ; θ ) \theta\leftarrow\theta+\beta\cdot\tilde{\boldsymbol{g}}(s,a;\boldsymbol{\theta}) θ←θ+β⋅g~(s,a;θ)。
- Actor-critic 用价值网络 q ( s , a ; w ) q(s,a;\boldsymbol{w}) q(s,a;w) 近似 Q π ( s , a ) Q_{\pi}(s,a) Qπ(s,a), 从而把 g ( s , a ; θ ) g(s,a;\boldsymbol{\theta}) g(s,a;θ) 近似成:
g ^ ( s , a ; θ ) ≜ q ( s , a ; w ) ⋅ ∇ θ ln π ( a ∣ s ; θ ) \widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta})\:\triangleq\:q(s,a;\boldsymbol{w})\:\cdot\:\nabla_{\boldsymbol{\theta}}\ln\pi(a\:|\:s;\:\boldsymbol{\theta}) g (s,a;θ)≜q(s,a;w)⋅∇θlnπ(a∣s;θ)
Actor-critic 用 SARSA 算法更新价值网络 q q q, 用梯度上升更新策略网络 : θ ← θ + β ⋅ g ^ ( s , a ; θ ) :\theta\gets\theta+\beta \cdot \widehat{\boldsymbol{g}}(s,a;\boldsymbol{\theta}) :θ←θ+β⋅g (s,a;θ)。
后记
截至2024年1月27日17点25分,学习完强化学习中的Actor-Critic算法。