前言
约数也是很重要的基础数学知识,希望大家能够完全掌握!!!
一、约数的知识
简介
约数,又称因数。整数a除以整数b(b≠0) 除得的商正好是整数而没有余数,就说a能被b整除,或b能整除a。a称为b的倍数,b称为a的约数。在大学之前,"约数"一词所指的一般只限于正约数。约数和倍数都是二元关系的概念,不能孤立地说某个整数是约数或倍数。一个整数的约数是有限的。同时,它可以在特定情况下成为公约数。
范例
在自然数(0和正整数)的范围内,
4的正约数有:1、2、4。
6的正约数有:1、2、3、6。
10的正约数有:1、2、5、10。
12的正约数有:1、2、3、4、6、12。
15的正约数有:1、3、5、15。
18的正约数有:1、2、3、6、9、18。
20的正约数有:1、2、4、5、10、20。
注意:一个数的约数必然包括1及其本身。
相关概念
如果一个数c既是数a的因数,又是数b的因数,那么c叫做a与b的公因数。
两个数的公因数中最大的一个,叫做这两个数的最大公因数。
约数,也叫因数。
二、例题及模板
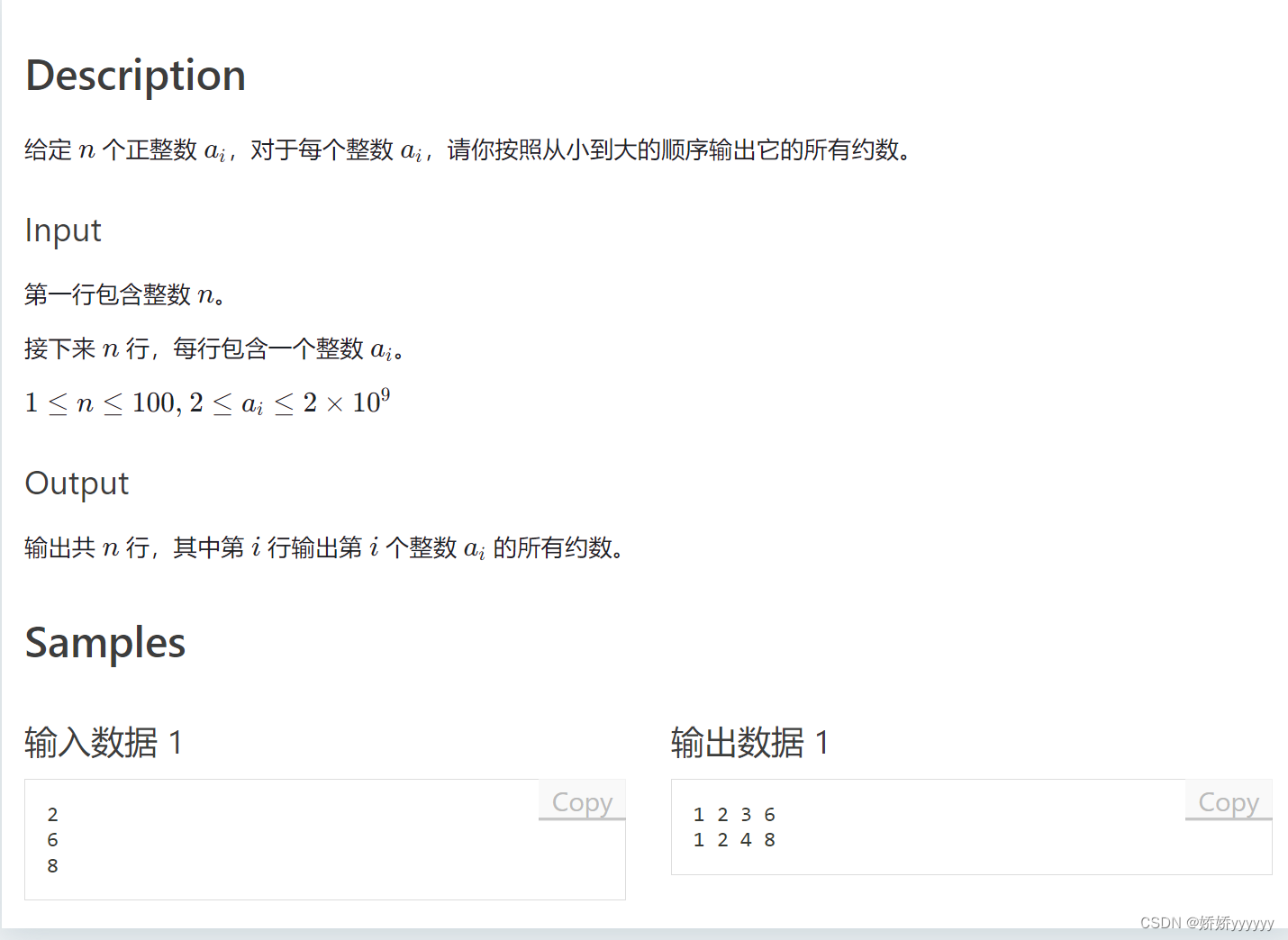
1.试除法求约数
模板:
vector<int> get_divisors(int x)
{
vector<int> res;
for (int i = 1; i <= x / i; i ++ )
if (x % i == 0)
{
res.push_back(i);
if (i != x / i) res.push_back(x / i);
}
sort(res.begin(), res.end());
return res;
}AC代码:
#include <bits/stdc++.h>
using namespace std;
void solve(int n)
{
vector<int> res;
for (int i = 1; i <= n / i; i ++ )
{
if (n % i == 0)
{
res.push_back(i);
if (i != n / i) res.push_back(n / i);
}
}
sort(res.begin(), res.end());
for (auto &i : res)
printf("%d ", i);
puts("");
}
int main()
{
int m;
scanf("%d", &m);
while (m -- )
{
int x;
scanf("%d", &x);
solve(x);
}
return 0;
}
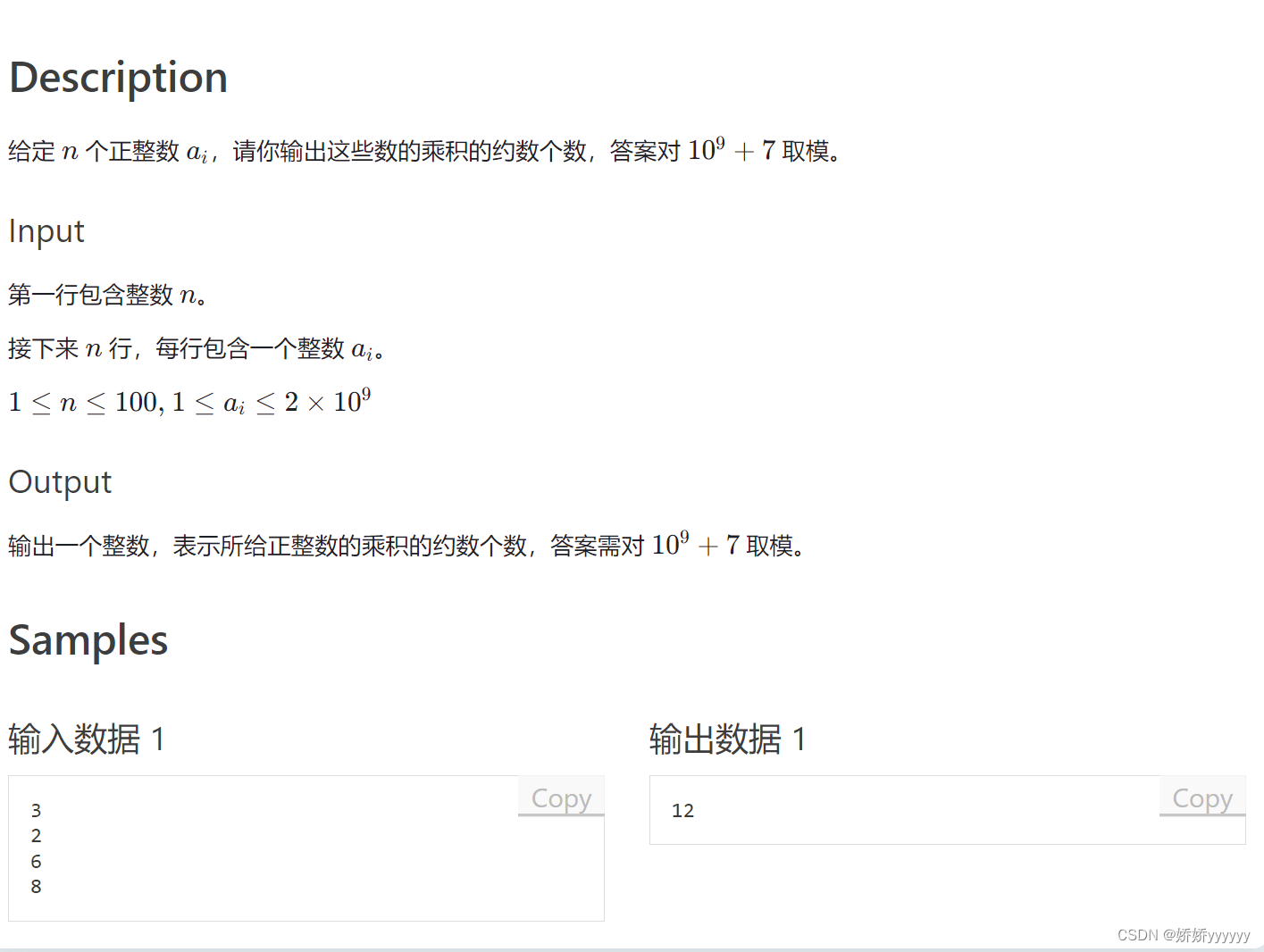
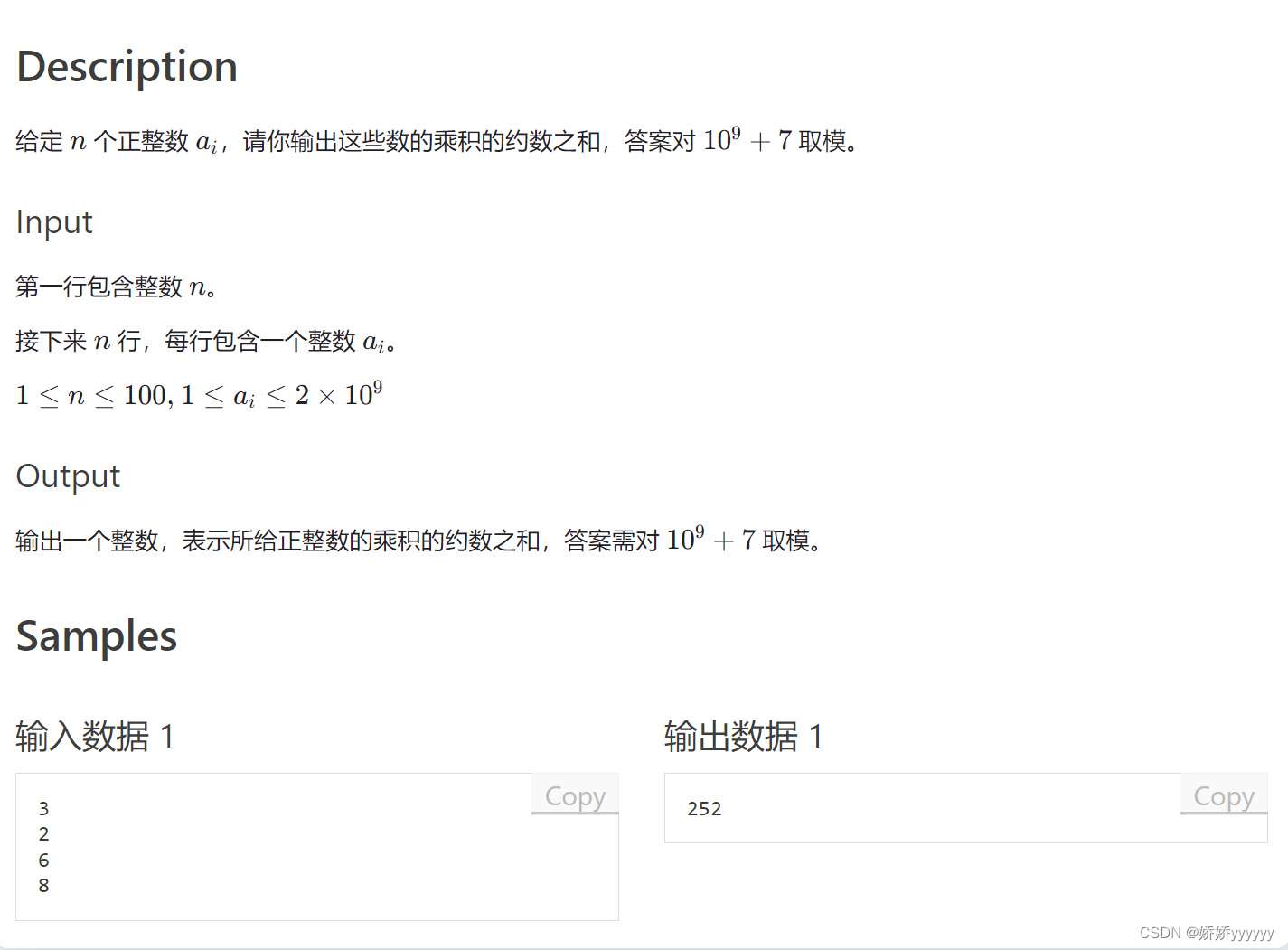
2.约数个数和约数之和
模板:
如果 N = p1^c1 * p2^c2 * ... *pk^ck
约数个数: (c1 + 1) * (c2 + 1) * ... * (ck + 1)
约数之和: (p1^0 + p1^1 + ... + p1^c1) * ... * (pk^0 + pk^1 + ... + pk^ck)约数个数:
约数之和
AC代码:
1约数个数:
#include <bits/stdc++.h>
using namespace std;
const int P = 1e9 + 7;
using LL = long long ;
unordered_map<int, int> primes;
void solve(int n) // 分解质因子
{
for (int i = 2; i <= n / i; i ++ )
{
while (n % i == 0)
{
primes[i] ++ ;
n /= i;
}
}
if (n > 1) primes[n] ++ ;
}
int main()
{
int m;
scanf("%d", &m);
while (m -- )
{
int x;
scanf("%d", &x);
solve(x);
}
LL ans = 1;
for (auto &it : primes)
ans = ans * (it.second + 1) % P;
printf("%lld\n", ans);
return 0;
}
2约数之和:
#include <bits/stdc++.h>
using namespace std;
const int P = 1e9 + 7;
using LL = long long ;
unordered_map<int, int> primes;
void solve(int n) // 分解质因子
{
for (int i = 2; i <= n / i; i ++ )
{
while (n % i == 0)
{
primes[i] ++ ;
n /= i;
}
}
if (n > 1) primes[n] ++ ;
}
int main()
{
int m;
scanf("%d", &m);
while (m -- )
{
int x;
scanf("%d", &x);
solve(x);
}
LL ans = 1;
for (auto &it : primes)
{
// p是质因子,s是该质因子的个数
LL p = it.first, s = it.second, t = 1;
while (s -- )
t = (t * p + 1) % P;
ans = ans * t % P;
}
printf("%lld\n", ans);
return 0;
}
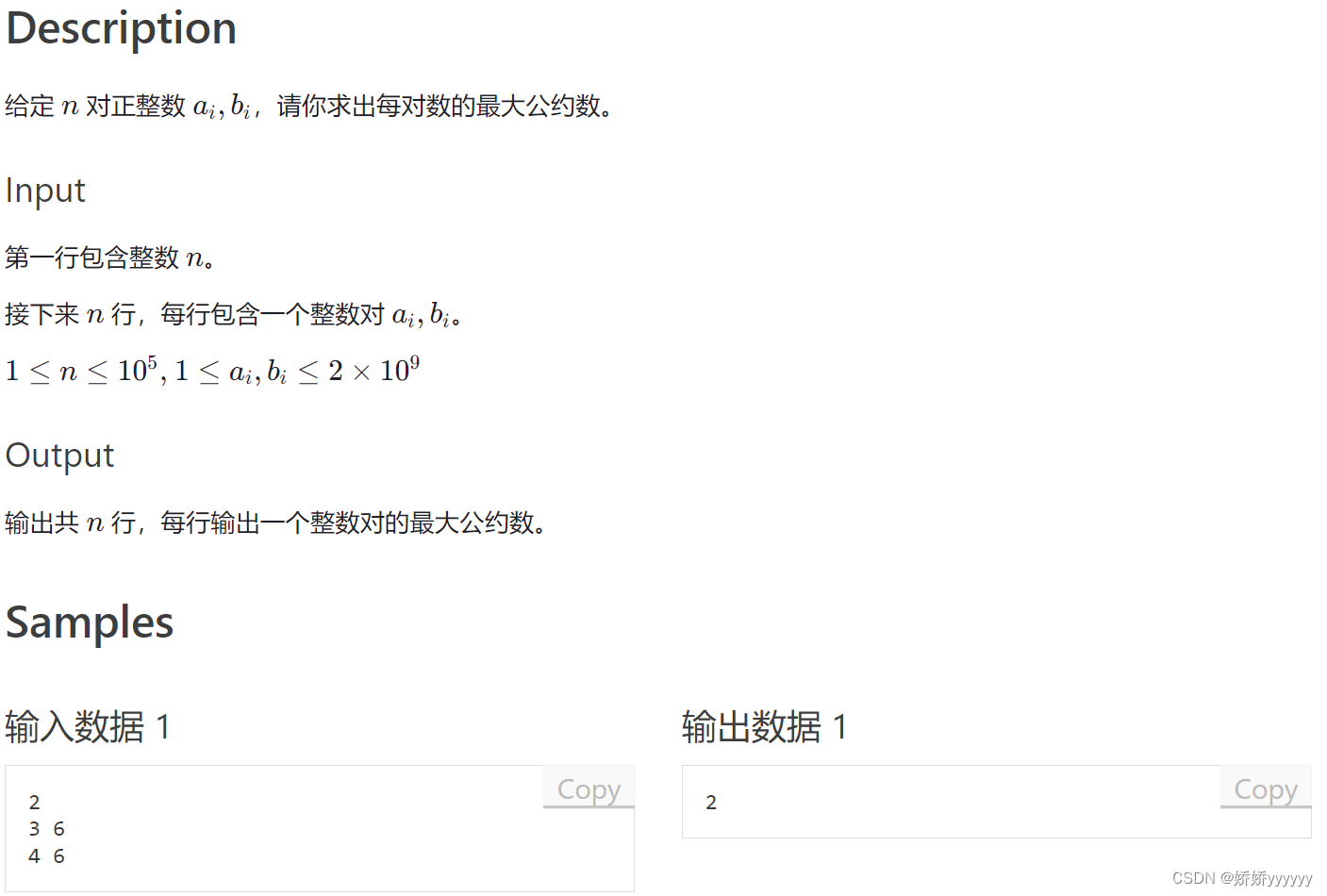
3、最大公约数
模板:
int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}AC代码:
#include <bits/stdc++.h>
using namespace std;
inline int gcd(int a, int b)
{
return b ? gcd(b, a % b) : a;
}
int main()
{
int m;
scanf("%d", &m);
while (m -- )
{
int a, b;
scanf("%d%d", &a, &b);
printf("%d\n", gcd(a, b));
}
return 0;
}