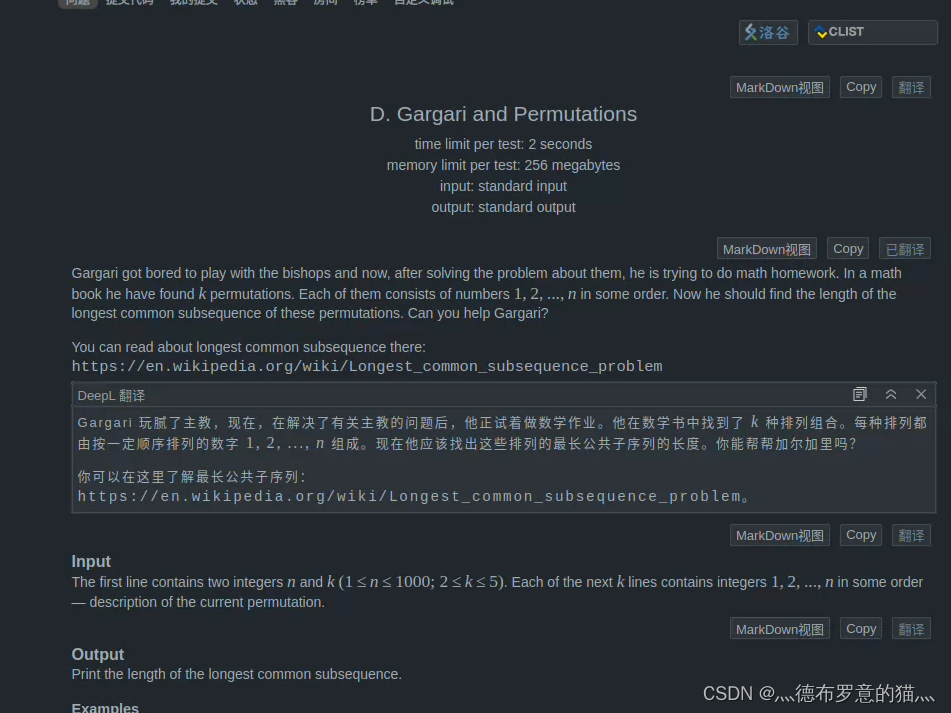
很好玩的一道类似LCS的DP 问题

定义dp(i) 为考虑最后一个字符串，且选择a（i）得到的最大LIS值

然后枚举所有小于i的位置，可以更新的条件是 所有的字符串中都有a[j]<a[i] 这个用map一处理就好了

#include<bits/stdc++.h>
using namespace std;
using ll = long long;
const int N = 3e5+10;

int n,m;
map<int,int>mp[10];
int a[N];
int dp[N];
void solve()
{	

	cin>>n>>m;
	for(int i=1;i<=m-1;i++)
	 for(int j=1;j<=n;j++){
	 	int x;cin>>x;mp[i][x] = j;
	 }
	 
	for(int i=1;i<=n;i++)cin>>a[i];
	for(int i=1;i<=n;i++)dp[i] = 1;
	int ans = 1;
	for(int i=1;i<=n;i++){
		for(int j=1;j<i;j++){
		  bool st = true;
		  for(int k=1;k<=m-1;k++)//mp[k][a[j]]<mp[k][a[i]]
		 	if(mp[k][a[j]]>mp[k][a[i]])st = false;	
			
		  if(st)dp[i] = max(dp[i],dp[j]+1);
	 }		
	 ans  = max(ans,dp[i]);
	}
	
	//for(int i=1;i<=n;i++)cout<<dp[i]<<" "<<" \n"[i==n];

	 
	 
	 cout<<ans<<"\n";
		

	
	
}

int main()
{
	ios::sync_with_stdio(0),cin.tie(0),cout.tie(0);
	int _;_ = 1;
	while(_--)solve();
}