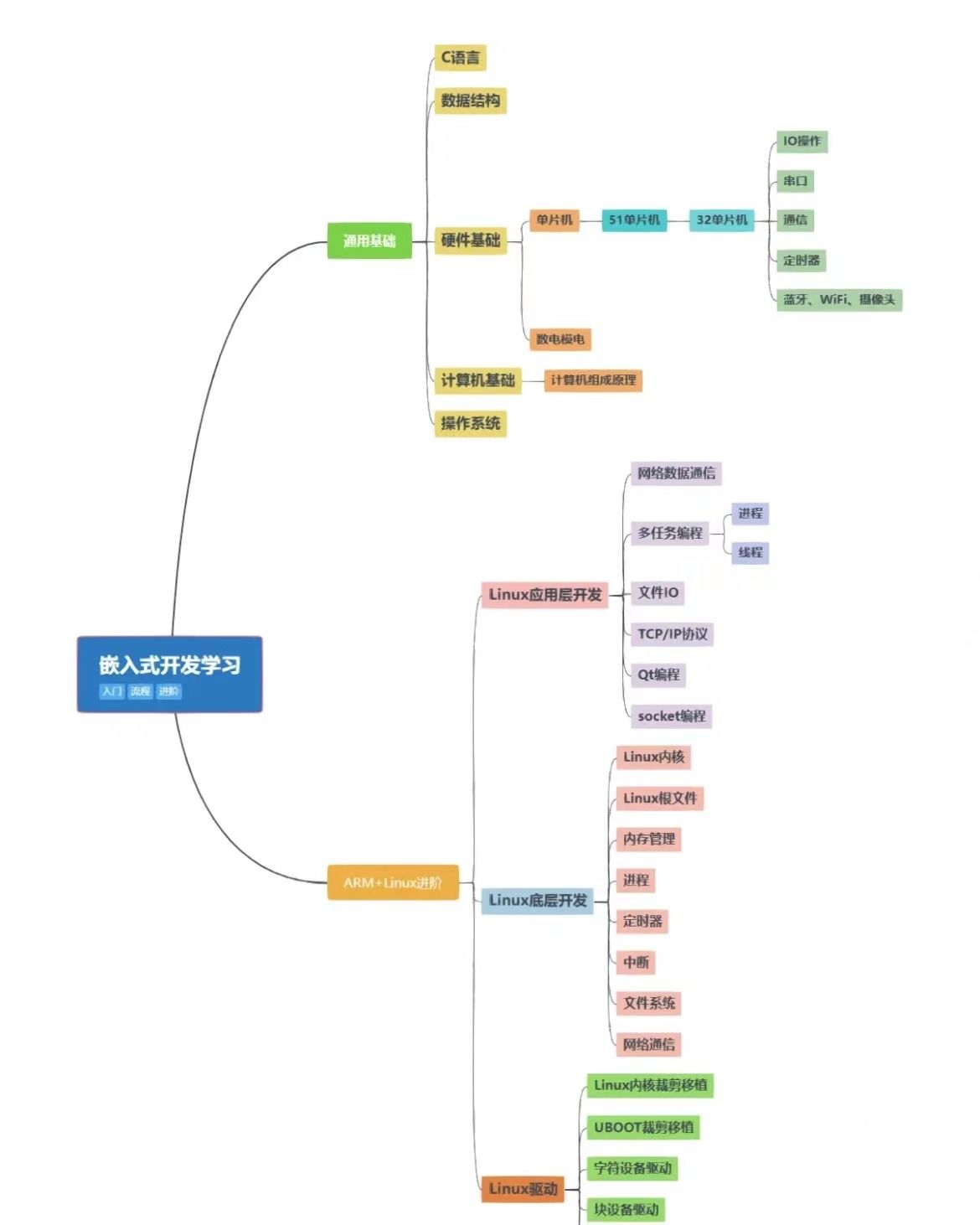
地图染色与时间表制定
“优化问题中的颜色选择和课程安排:最小颜色数和时间冲突的解决”
设想你正在绘制一幅地图,地图上分成了若干区域,你希望为这些区域选取颜色。你可能想选用尽可能少的颜色,但同时还希望避免任意两块相邻区域使用相同的颜色。再设想你正在安排大学课程的时间表。课程有很多门,但可供安排的总时间段有限,所以会有某些门课程时间冲突。哪些学生选了哪些课程已经登记在列,你希望尽可能合理安排,仅当两门课程没有学生同时选择时才可以时间冲突。
“图论中的颜色分配和时间冲突问题:对象属性的数学模型”
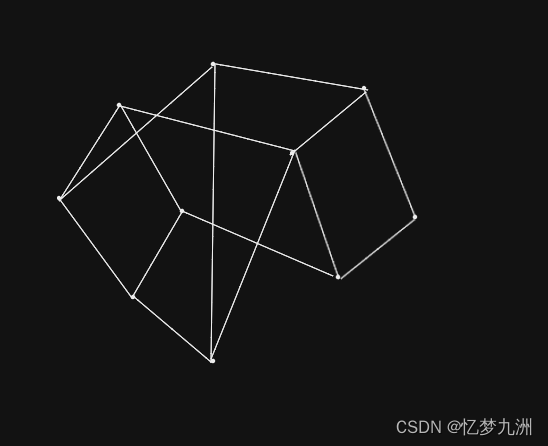
这两个问题看似截然不同,但一种合理的模型能够说明,从数学的观点来看它们其实是一样的。在这两个问题中,都需要给一些对象(国家、课程)赋予一些属性(颜色、时间)。对象中有某些两两组合(相邻的国家,不能冲突的课程)是不能相容的,也就是说它们不能被赋予相同的属性。在这两个问题中,我们其实并不关心具体的对象是什么、要赋予的属性是什么,所以我们也可以仅用点来表示它们。为了表示那些不相容的成对的点,我们可以将它们用线段连结起来。这样一组边和边连结起来的点的集合,就是“图”这种数学结构。下图给出了一个简单的例子。通常称图中的点为顶点,称线段为边。
“统一问题:图论中的顶点分组问题和模型简化的优势”
一旦我们将问题用这种形式表示出来,我们在两个例子中的任务就统一为:将顶点分成尽可能少的几组,使得每组中不包含由同一条边相连的两顶点。(上图所表示的图可以分成三组,但不可能分成两组。)这也就说明了使模型尽可能简化的另一个充足理由:如果幸运的话,同样的模型可以用来一次性研究很多不同的现象。
总结
地图染色问题和时间表制定问题在数学观点上可以统一为图论中的顶点分组问题。无论是为地图的不相邻区域选取颜色,还是为课程安排时间表,我们都需要将对象(区域或课程)赋予特定属性(颜色或时间),并确保相邻的对象不具有相同的属性。通过将问题转化为图的形式,我们可以用顶点和边来表示对象和对象之间的关系。我们的目标是将顶点分成尽可能少的组,使得每组中不存在由同一条边相连的顶点。这种统一模型的好处是,我们可以利用图论的相关算法和技巧来解决这类问题。同时,通过简化模型,我们可以更广泛地应用同一套方法,研究不同领域的现象。