文章目录
- 题目
- 考察点
- 代码实现
- 实现总结
- 扩展
- 用迭代的方式判断是否为对称二叉树
- 递归和迭代的对比
- 可能的扩展提问
坚持刷题,老年痴呆追不上我,今天真的好累,就不难为自己了,刷个简单级别的吧:对称二叉树
题目
101.对称二叉树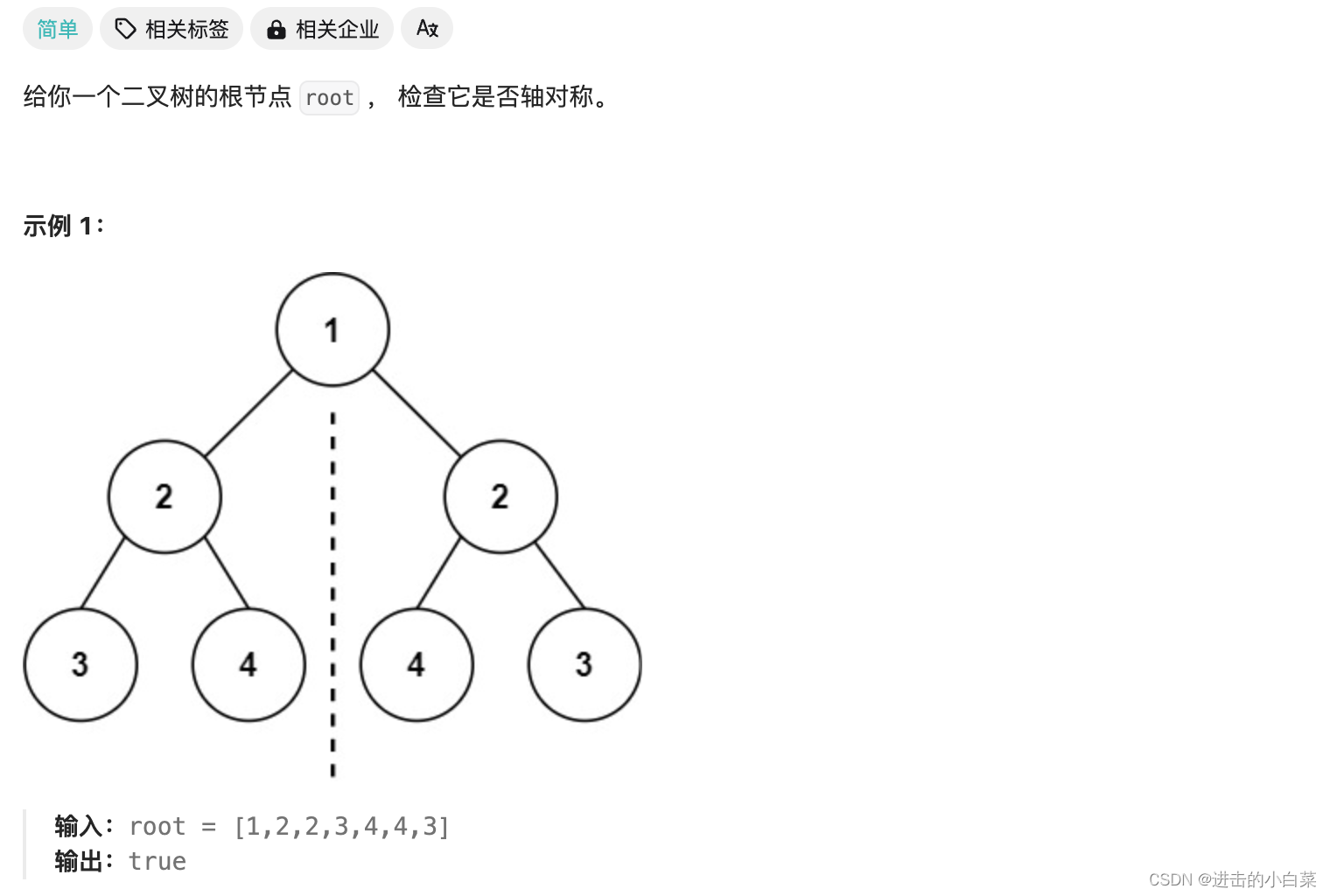
考察点
- 递归能力: 能否使用递归来解决问题。
- 树的基本操作:能否正确地访问节点的值,左子树,右子树等。
- 边界条件处理: 能否正确处理空树的情况。
- 镜像对称性的理解: 能否理解对称二叉树的定义。
- 时间和空间复杂度: 解决问题的方法是否具有合理的时间和空间复杂度。
代码实现
class TreeNode {
int val;
TreeNode left, right;
public TreeNode(int val) {
this.val = val;
this.left = this.right = null;
}
}
public class SymmetricBinaryTree {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true; // 空树是对称的
}
return isMirror(root.left, root.right);
}
private boolean isMirror(TreeNode left, TreeNode right) {
if (left == null && right == null) {
return true; // 左右子树都为空,是对称的
}
if (left == null || right == null) {
return false; // 一个为空,一个不为空,不对称
}
// 判断当前节点值相等,并且左子树的左子树与右子树的右子树镜像对称,
// 且左子树的右子树与右子树的左子树镜像对称
return (left.val == right.val) &&
isMirror(left.left, right.right) &&
isMirror(left.right, right.left);
}
public static void main(String[] args) {
// 创建一个对称二叉树的例子
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(2);
root.left.left = new TreeNode(3);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(4);
root.right.right = new TreeNode(3);
SymmetricBinaryTree checker = new SymmetricBinaryTree();
boolean isSymmetric = checker.isSymmetric(root);
System.out.println("Is the tree symmetric? " + isSymmetric);
}
}
实现总结
- 边界条件处理: 空树是对称的。
- 镜像对称性的理解: 要正确理解对称二叉树的定义,即左子树和右子树镜像对称。
- 时间复杂度:O(n)。递归的实现是通过深度优先遍历,每个节点只访问一次。在最坏情况下,需要访问二叉树的所有节点,因此时间复杂度是线性的,与节点数成正比。
- 空间复杂度:O(n)。空间复杂度主要取决于递归调用的深度,因为每一层递归调用都会占用一定的栈空间。在这个对称二叉树的递归实现中,递归调用的深度最多为树的高度。对于平衡二叉树来说,树的高度近似 log(n),其中 n 是节点数。但在最坏情况下,如果二叉树是一条链,树的高度就是节点数 n。
扩展
用迭代的方式判断是否为对称二叉树
使用迭代的方式通常需要借助队列(Queue)来模拟递归的过程。具体思路是利用队列按层遍历二叉树,并逐层判断是否对称:
import java.util.LinkedList;
import java.util.Queue;
class TreeNode {
int val;
TreeNode left, right;
public TreeNode(int val) {
this.val = val;
this.left = this.right = null;
}
}
public class SymmetricBinaryTree {
public boolean isSymmetric(TreeNode root) {
if (root == null) {
return true; // 空树是对称的
}
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root.left);
queue.offer(root.right);
while (!queue.isEmpty()) {
TreeNode leftNode = queue.poll();
TreeNode rightNode = queue.poll();
if (leftNode == null && rightNode == null) {
continue; // 左右子树都为空,继续下一层比较
}
if (leftNode == null || rightNode == null) {
return false; // 一个为空,一个不为空,不对称
}
if (leftNode.val != rightNode.val) {
return false; // 节点值不相等,不对称
}
// 将左子树的左节点、右子树的右节点和左子树的右节点、右子树的左节点加入队列,以便下一层比较
queue.offer(leftNode.left);
queue.offer(rightNode.right);
queue.offer(leftNode.right);
queue.offer(rightNode.left);
}
return true;
}
public static void main(String[] args) {
// 创建一个对称二叉树的例子
TreeNode root = new TreeNode(1);
root.left = new TreeNode(2);
root.right = new TreeNode(2);
root.left.left = new TreeNode(3);
root.left.right = new TreeNode(4);
root.right.left = new TreeNode(4);
root.right.right = new TreeNode(3);
SymmetricBinaryTree checker = new SymmetricBinaryTree();
boolean isSymmetric = checker.isSymmetric(root);
System.out.println("Is the tree symmetric? " + isSymmetric);
}
}
在这个实现中,我们使用一个队列来模拟递归的过程,不断将每一层的左子树和右子树的对应节点入队,并比较它们的值。如果出现不对称的情况,直接返回 false。最终,如果队列为空,则说明整个二叉树是对称的,返回 true。
递归和迭代的对比
| 方式 | 优势 | 劣势 |
|---|---|---|
| 递归 | 简洁、直观 、可读性好 | 栈空间占用,可能导致栈溢出 |
| 迭代 | 性能较好 | 代码可能相对冗长,需要显式数据结构维护 |
- 如果树规模较小且对代码简洁性有要求,可以选择递归。 递归在解决对称二叉树问题时通常能够提供简洁而清晰的解决方案。
- 如果树规模较大或者对性能有要求,可以选择迭代。 迭代通常在大规模数据的情况下性能更好,尤其是当树的深度较大时。
可能的扩展提问
是否可以对递归实现进行优化,减少不必要的调用或重复计算呢?
早期终止条件: 在递归函数的开始,可以加入一些早期终止条件,以尽早地判断当前子树是否不对称,从而避免进一步的递归调用。例如,如果左右节点值不相等,可立即返回 false。
private boolean isMirror(TreeNode left, TreeNode right) {
if (left == null && right == null) {
return true;
}
if (left == null || right == null || left.val != right.val) {
return false;
}
// 继续递归判断
return isMirror(left.left, right.right) && isMirror(left.right, right.left);
}
还有没有其他或者更好的优化思路呢🤔,评论区一起开麦讨论🎤吧