本文主要分为两部分,第一部分介绍什么是GCN,第二部分将进行详细的数学推导。
一、什么是GCN
1、GCN 概述

本文讲的GCN 来源于论文:SEMI-SUPERVISED CLASSIFICATION WITH GRAPH CONVOLUTIONAL NETWORKS,这是在GCN领域最经典的论文之一。
我们可以根据这个GCN的图看到,一个拥有C个input channel的graph作为输入,经过中间的hidden layers,得到F个 output channel的输出。(注意本文讲的图都特指无向无权重的图。)
图卷积网络主要可以由两个级别的作用变换组成:
(1)graph level
例如说通过引入一些形式的pooling 操作 (see, e.g. Duvenaud et al., NIPS 2015),然后改变图的结构。但是本次讲过GCN并没有进行这个级别的操作。所以看到上图我们的网络结构的输出和输出的graph的结构是一样的。
(2)node level
通常说node level的作用是不改变graph的结构的,仅通过对graph的特征/(features/signals)X作为输入:一个的矩阵(
: 输入图的nodes的个数,
输入的特征维度) ,得到输出
:一个
的矩阵(
输出的特征维度)。
a) 一个特征描述(feature description) : 指的是每个节点
的特征表示
b) 每一个graph 的结构都可以通过邻接矩阵 表示(或者其他根据它推导的矩阵)
我们可以很容易的根据一个邻接矩阵重构出一个graph。 例如下图:,其中
代表节点,
代表边

我们通过构造的矩阵可以得到邻接矩阵
, 其中
如果节点
和节点
相连,否则
, 我们根据graph可以得到
, 同理通过
也可以得到graph 的结构。

所以网络中间的每一个隐藏层可以写成以下的非线性函数:
其中输入层, 输出层
,
是层数。 不同的GCN模型,采用不同
函数。
2、模型定义
论文中采用的函数如下:
刚开始看的时候,都会被吓到!这个函数未免也太抽象了。但是我们先了解一下它在起的作用,然后再从头一步一步引出这个公式,以及为什么它起到了这些作用。
首先物理上它起的作用是,每一个节点下一层的信息是由前一层本身的信息以及相邻的节点的信息加权加和得到,然后再经过线性变换以及非线性变换
。
我们一步一步分解,我们要定义一个简单的 函数,作为基础的网络层。
我们可以很容易的采用最简单的层级传导( layer-wise propagation )规则
我们直接将做矩阵相乘,然后再通过一个权重矩阵
做线性变换,之后再经过非线性激活函数
, 比如说 ReLU,最后得到下一层的输入
。
我们需要特别注意的是做矩阵相乘,这代表了什么意思呢?
我们先看看,对于下图。

假设每个节点, 那么在经过矩阵相乘之后,它会变成什么呢。
输入层的 , 根据矩阵的运算公式我们可以很容易地得到下一层的该节点的表示
, 也很容易发现
,而
就是节点1的相邻节点。具体计算结果可以参考下面的代码。
A = torch.tensor([
[0,1,0,0,1,0],
[1,0,1,0,1,0],
[0,1,0,1,0,0],
[0,0,1,0,1,1],
[1,1,0,1,0,0],
[0,0,0,1,0,0]
])
H_0 = torch.tensor([
[1,1,1,1],
[2,2,2,2],
[3,3,3,3],
[4,4,4,4],
[5,5,5,5],
[6,6,6,6]
])
A.matmul(H_0)
>>>tensor([[ 7, 7, 7, 7],
[ 9, 9, 9, 9],
[ 6, 6, 6, 6],
[14, 14, 14, 14],
[ 7, 7, 7, 7],
[ 4, 4, 4, 4]])
所以我们直到就是把通过邻接矩阵快速的方式,快速将相邻的节点的信息相加得到自己下一层的输入。
但是这就完美了吗?
- 问题一:我们虽然获得了周围节点的信息了,但是自己本身的信息却没了(除非自己有一条边指向自己)。
我们采用的解决方案是,对每个节点手动增加一条self-loop 到每一个节点,即 , 其中
是单位矩阵identity matrix。
- 问题二:从上面的结果也可以看出,在经过一次的
矩阵变换后,得到的输出会变大,即特征向量
的scale会改变,在经过多层的变化之后,将和输入的scale差距越来越大。
所以我们是否可以将邻接矩阵做归一化使得最后的每一行的加和为1,使得
获得的是weighted sum。
我们可以将的每一行除以行的和,这就可以得到normalized的
。而其中每一行的和,就是每个节点的度degree。用矩阵表示则为:
, 对于
我们还是按照上面图的graph来看。
import torch
A = torch.tensor([
[0,1,0,0,1,0],
[1,0,1,0,1,0],
[0,1,0,1,0,0],
[0,0,1,0,1,1],
[1,1,0,1,0,0],
[0,0,0,1,0,0]
], dtype=torch.float32)
D = torch.tensor([
[2,0,0,0,0,0],
[0,3,0,0,0,0],
[0,0,2,0,0,0],
[0,0,0,3,0,0],
[0,0,0,0,3,0],
[0,0,0,0,0,1],
], dtype=torch.float32)
hat_A = D.inverse().matmul(A)
>>>hat_A
tensor([[0.0000, 0.5000, 0.0000, 0.0000, 0.5000, 0.0000],
[0.3333, 0.0000, 0.3333, 0.0000, 0.3333, 0.0000],
[0.0000, 0.5000, 0.0000, 0.5000, 0.0000, 0.0000],
[0.0000, 0.0000, 0.3333, 0.0000, 0.3333, 0.3333],
[0.3333, 0.3333, 0.0000, 0.3333, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 1.0000, 0.0000, 0.0000]])但是在实际运用中我们采用的是对称的normalization:
对于
这跟Laplacian Matrix 有关,下一部分会介绍。 我们可以发现
D_minus_sqrt = D.inverse().sqrt()
D_minus_sqrt.matmul(A).matmul(D_minus_sqrt)
>>>
tensor([[0.0000, 0.4082, 0.0000, 0.0000, 0.4082, 0.0000],
[0.4082, 0.0000, 0.4082, 0.0000, 0.3333, 0.0000],
[0.0000, 0.4082, 0.0000, 0.4082, 0.0000, 0.0000],
[0.0000, 0.0000, 0.4082, 0.0000, 0.3333, 0.5774],
[0.4082, 0.3333, 0.0000, 0.3333, 0.0000, 0.0000],
[0.0000, 0.0000, 0.0000, 0.5774, 0.0000, 0.0000]])
把这两个tricks结合起来,我们可以得到
其中 ,
是
的degree matrix。 而
是对
做了一个对称的归一化。
二、数学推导
1、Graph Laplacian
首先我们表示一个graph的方式有很多,我们可以用邻接矩阵,也可以用Incidence matrix。 这个matrix 中,每一行表示一个边,每一列表示一个节点。每一行中,边的节点的起点用记为1,边的终点记为-1。 我们将这个metrix 记为 , 具体如下图。

那么 graph Laplacian 定义为:
C = torch.tensor([
[1,-1,0,0],
[1,0,-1,0],
[1,0,0,-1],
[0,-1,1,0],
[0,0,1,-1],
[0,-1,0,1],
])
C.T.matmul(C)
>>>tensor(
[[ 3, -1, -1, -1],
[-1, 3, -1, -1],
[-1, -1, 3, -1],
[-1, -1, -1, 3]])我们可以发现,对角线的值![]() , 其中如果
, 其中如果 , 则其积 = 0,如果
或者
, 则其积 = 1。所以我们可以知道对角线代表的是每个节点的度(Degree)
对于非对角线的值 ![]() , 我们可以看出来,如果节点
, 我们可以看出来,如果节点 和
没有相连,那么
否则
, 于是知道非对角线的值就是邻接矩阵的负值。
所以我们可以推导得到
如下图(注意这边W表示的是邻接矩阵)

总结来说:

具体计算参考下面的代码
C = torch.tensor([
[-1,1,0,0,0,0], # 1-2
[-1,0,0,0,1,0], # 1-5
[0,-1,1,0,0,0], # 2-3
[0,-1,0,0,1,0], # 2-5
[0,0,-1,1,0,0], # 3-4
[0,0,0,-1,1,0], # 4-5
[0,0,0,-1,0,1], # 5-6
])
C.T.matmul(C)
>>>
tensor([[ 2, -1, 0, 0, -1, 0],
[-1, 3, -1, 0, -1, 0],
[ 0, -1, 2, -1, 0, 0],
[ 0, 0, -1, 3, -1, -1],
[-1, -1, 0, -1, 3, 0],
[ 0, 0, 0, -1, 0, 1]])我们需要知道 laplacian 的性质:
-
是对称矩阵
有实数的,非负的特征值(eigen values)
有实数的,正交的特征矩阵(eigen vectors), i.e.
对此,我们假设 的特征值为
特征向量为
:

- 对于特征值我们有
- 对称归一化的Laplacian (Symmetric normalized Laplacian)
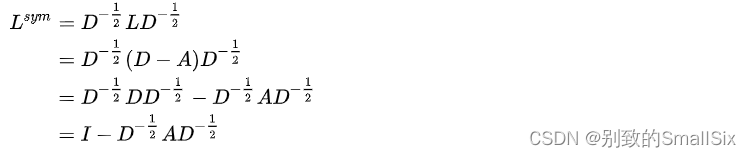
其元素值,对角线为1,非对角线为

我们要知道两个函数的卷积可以由以下公式得到,具体参考
![]()
其中 代表傅立叶变换
而Graph Fourier变换对应的就是以下:
![]()
其中Graph Fourier 逆变换对应的就是以下:
![]()
其中是laplacian
的特征矩阵 具体的对应关系:

我们知道普通的卷积公式:

那么相应的图卷积的公式为:

作为图的特征的filter,我们希望它的作用域跟CNN一样,都是在中心节点附近的区域,所以我们定义
是一个laplacian的函数
, 那么作用一次相当于传播一次周围邻居节点的信息。
又因为 , 所以我们可以把
看成是laplacian 特征值的函数
, 参数为
。
所以图卷积在Fourier域上可以表示为:
![]()
我们知道 需要先计算laplacian matrix
的特征值,这涉及到大量的矩阵运算,所以文章借用了Chebyshev polynomials进行近似计算:

- 其中
,
代表的是
次Laplacian,即它取决于中心节点的最近的
order 的邻居节点(邻居节点和中心节点的距离最大为K)。
, 其中
以及
。
我们回到最初的图卷积计算:

其中
我们知道论文中采用的传播邻居层数为1, 所以取 , 并且我们假设
, 可以得到:

实际运用中,为了防止overfitting以及减少操作,我们令
得到:
![]()
我们令 , 以及
![]()
得到:
![]()
再加上激活函数, 我们获得了
![]()
其中对应输入
,
对应参数
。
三、ref
- https://en.wikipedia.org/wiki/Laplacian_matrix
- T. N. Kipf, M. Welling, Semi-Supervised Classification with Graph Convolutional Networks(ICLR 2017) [Link, PDF (arXiv), code, blog]
- https://math.stackexchange.com/questions/1113467/why-laplacian-matrix-need-normalization-and-how-come-the-sqrt-of-degree-matrix