所有的LeetCode题解索引，可以看这篇文章——【算法和数据结构】LeetCode题解。

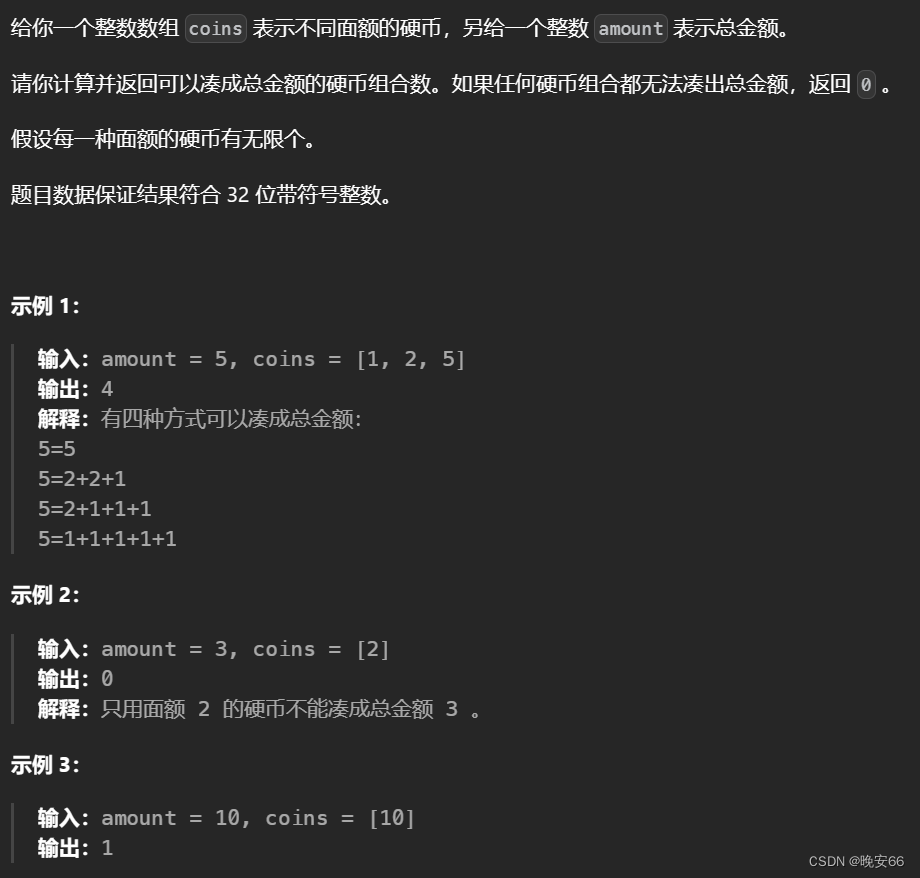
一、题目

二、解法

  思路分析：本题的硬币是无数的，因此本题可以抽象成一个完全背包问题。完全背包和01背包的不同之处在于完全背包式从前往后遍历的。在本题的完全背包问题中，amount代表背包的最大重量，coins数组代表物品的重量和价值。$dp[i]$代表背包重量为$i$时，硬币凑成的组合（2 2 1 和 2 1 2这两个是不同排列，但是它们属于一个组合）总数为$dp[i]$。我们将$dp[0]$初始化为1，不需要找零也是一种组合。$dp[j]$可以由$dp[j-coins[i]]$得出。因为求的是组合总数，所以递归公式为：$dp[j]+=dp[j-coins[i]]$。特别需要注意的是，因为题目要求的是组合数而不是排列数，所以本题循环采取的是先遍历物品，后遍历背包容量的形式。如果说题目要求的是排列数，例如【算法与数据结构】377、LeetCode组合总和 Ⅳ这道题要求的就是排列数，遍历顺序则需要用先遍历背包容量，后遍历物品的方式，保证每个背包容量所有的排列数都被遍历到。
  程序如下：

class Solution {
public:
	int change(int amount, vector<int>& coins) {
		vector<int>dp(amount + 1, 0);
		dp[0] = 1;
		// 先遍历物品，再遍历背包
		for (int i = 0; i < coins.size(); i++) { // 遍历物品
			for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
				dp[j] += dp[j - coins[i]];
			}
		}
		return dp[amount];
	}
};

复杂度分析：

• 时间复杂度： $O(n\ast m)$， n=amount，m是coin数组的大小。
• 空间复杂度：$O(n)$。

三、完整代码

# include <iostream>
# include <vector>
# include <algorithm>
using namespace std;

class Solution {
public:
	int change(int amount, vector<int>& coins) {
		vector<int>dp(amount + 1, 0);
		dp[0] = 1;
		// 先遍历物品，再遍历背包
		for (int i = 0; i < coins.size(); i++) { // 遍历物品
			for (int j = coins[i]; j <= amount; j++) { // 遍历背包容量
				dp[j] += dp[j - coins[i]];
			}
		}
		return dp[amount];
	}
};

int main() {
	Solution s1;
	int amount = 5;
	vector<int> coins = { 1, 2, 5 };
	int result = s1.change(amount, coins);
	cout << result << endl;
	system("pause");
	return 0;
}

end