目录

1.1梯度下降

1.2随机梯度下降

1.3小批量随机梯度下降

1.4冲量法

1.5 Adam

---

损失值也就是预测值与真实值之间的差值是f(x)，x是所有超参数组成的一条向量，c是可以限制的，比如说权重大于等于0。

使用迭代优化算法求解一般只能保证找到局部最小值，因为一到局部最小的地方，用梯度下降算法的话此时的梯度就已经等于0了。

凸集的意思就是在一个区域里面找一根线，这条线的任意一个点都在这个区域里面。

凸函数最简单的理解就是，在函数上画两个点，这两个点连起来，保证整个函数都在连线的下面。

1.1梯度下降

1.2随机梯度下降

随机梯度下降就是随机选取单个样本上的损失来近似全局的损失。单个样本损失梯度的期望等于全局损失梯度的均值，虽然有噪音，但是整体的方向是差不多的。

1.3小批量随机梯度下降

减小了方差就是减小了抖动，蓝色就是梯度下降，一开始就很好，紫色是随机梯度下降，随机梯度下降比梯度下降要慢的原因是，每次算一个样本用不了硬件的并行度，加批量。批量大小在一个合适的区间是比较好的。

1.4冲量法

也就是更平滑的改变方向，不要让方向变得过于大。原理就是不只是看当前时刻的梯度，也看过去时刻的梯度。如果和特别不一样的话，就会抵消掉一些，让变化不那么剧烈。如果取等于0.99的话，大概可以看过去几十个梯度的平均。如果样本比较大娶个0.99也是比较正常的。0.5就是看过去的两三个梯度。

1.5 Adam

Adam可以认为是非常平滑的SGD，非常平滑的话对学习率就不太敏感了。如果想去调参的话用sgd加其他的算法会比用Adam效果好一丁点。当t比较小的时候有用，修正t较小的时候偏零的趋势。t比较大的时候无所谓，因为是大于0小于1的，在t时刻很大的时候，就变成0了。所以修正是针对比较小的t做的。

重新调整的梯度是对每一个权重的维度除以梯度的平方的和（过去的所有梯度加起来），就把所有的特征都拉到一个比较平均的地方，这样好调学习率。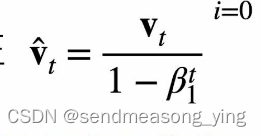，使得过去的梯度方向比较平滑，是使得每个维度的值都在合适的范围里面，做维度的调整。

Adam对学习率比较稳定，调参容易一点。