华南理工大学数字信号处理实验实验一（薛y老师版本）matlab源码

news2025/1/12 8:04:41

一、实验目的

1、加深对离散信号频谱分析的理解；

2、分析不同加窗长度对信号频谱的影响；

3、理解频率分辨率的概念，并分析其对频谱的影响；

4、窗长和补零对DFT的影响

实验源码：

第一题：

% 定义离散信号 x[n]
n = 0:1000; % 离散时间范围
x = cos(pi*n/10) + sin(pi*n/6) + cos(2*pi*n/5); % 信号定义

% 计算频谱
X = fft(x); % 应用离散傅里叶变换

% 绘制频谱图
f = (0:length(X)-1)*(1/length(X)); % 频率范围
figure(1);
plot(f, abs(X)); % 绘制频谱图
xlabel('Frequency'); % x轴标签
ylabel('Magnitude'); % y轴标签
title('Spectrum'); % 图标题

% 窗口长度为 N = 16
N1 = 16;
window1 = rectwin(N1); % 矩形窗口
x1 = x(1:N1) .* window1'; % 截取信号并应用窗口
X1 = fft(x1); % 计算频谱

% 窗口长度为 N = 60
N2 = 60;
window2 = rectwin(N2); % 矩形窗口
x2 = x(1:N2) .* window2'; % 截取信号并应用窗口
X2 = fft(x2); % 计算频谱

% 窗口长度为 N = 120
N3 = 120;
window3 = rectwin(N3); % 矩形窗口
x3 = x(1:N3) .* window3'; % 截取信号并应用窗口
X3 = fft(x3); % 计算频谱

pic1=[1:16];
pic2=[1:60];
pic3=[1:120];
% 绘制不同窗口长度截取后的频谱图
figure(2);
subplot(3, 1, 1);
stem(pic1, abs(X1));
xlabel('Frequency');
ylabel('Magnitude');
title('Spectrum (N = 16)');

subplot(3, 1, 2);
stem(pic2, abs(X2));
xlabel('Frequency');
ylabel('Magnitude');
title('Spectrum (N = 60)');

subplot(3, 1, 3);
stem(pic3, abs(X3));
xlabel('Frequency');
ylabel('Magnitude');
title('Spectrum (N = 120)');

% 窗口长度为 N = 120
N = 120;
n = 0:N-1;

% 矩形窗口
window_rect = rectwin(N);
x_rect = x(1:N) .* window_rect';
X_rect = fft(x_rect);

% 汉宁窗
window_hann = hann(N);
x_hann = x(1:N) .* window_hann';
X_hann = fft(x_hann);

% 黑曼窗
window_hamming = hamming(N);
x_hamming = x(1:N) .* window_hamming';
X_hamming = fft(x_hamming);

% 绘制不同窗口对频谱的影响
figure(3);
subplot(3, 1, 1);
stem(pic3, abs(X_rect));
xlabel('Frequency');
ylabel('Magnitude');
title('Spectrum (Rectangular Window)');

subplot(3, 1, 2);
stem(pic3, abs(X_hann));
xlabel('Frequency');
ylabel('Magnitude');
title('Spectrum (Hann Window)');

subplot(3,1,3);
stem(pic3, abs(X_hamming));
xlabel('Frequency');
ylabel('Magnitude');
title('Spectrum (Hamming Window)');

运行效果：

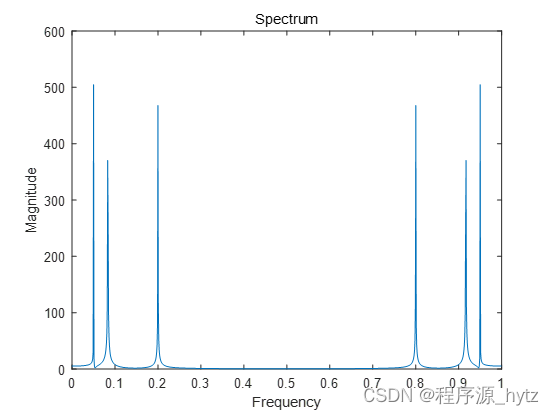
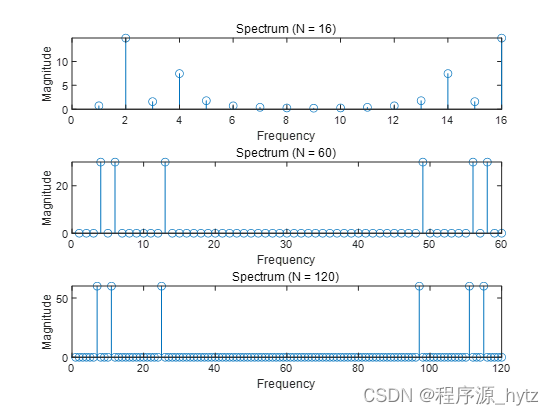
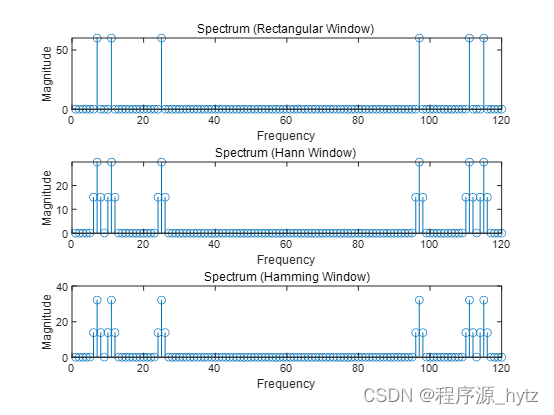
第二题：

（1）首先，我们需要确定对连续信号 x(t) 进行采样时的最大采样间隔和频域采样的最少采样点数，以满足要求的频率分辨率。

确定最大采样间隔：

根据奈奎斯特采样定理，连续信号的最大频率成分应小于采样频率的一半。在这种情况下，我们需要确定连续信号的最大频率成分。

给定的信号 x(t) 包含了三个频率成分：200 Hz、100 Hz 和 50 Hz。因此，连续信号的最大频率成分为 200 Hz。根据奈奎斯特采样定理，我们需要选择的采样频率应大于 2 * 200 Hz = 400 Hz。

所以，最大采样间隔为 T = 1 / 400 Hz = 0.0025 秒，即采样频率为 400 Hz。

确定频域采样的最少采样点数：

频域采样的最少采样点数取决于所需的频率分辨率和采样频率。在这种情况下，要求的频率分辨率为 1 Hz，采样频率为 400 Hz。

根据频率分辨率和采样频率的关系，最少采样点数 N 可以通过以下公式计算：

N = 采样频率 / 频率分辨率

N = 400 Hz / 1 Hz = 400

（2）（3）

% 参数设置
Fs = 400; % 采样频率
T = 1/Fs; % 采样间隔
N = 400; % 采样点数
f = (0:N-1) * Fs/N; % 频率轴

% 生成信号
t = (0:N-1) * T; % 时间轴
x = cos(200*pi*t) + sin(100*pi*t) + cos(50*pi*t); % 信号

% 进行频谱分析
X = abs(fft(x, N)); % DFT

% 绘制幅频特性
figure;
plot(f, X);
xlabel('Frequency (Hz)');
ylabel('Magnitude');
title('Amplitude Spectrum');

% 分析频域采样点数对频谱的影响
figure;
N_values = [100, 200, 400, 800]; % 不同的采样点数
for i = 1:length(N_values)
    N = N_values(i);
    f = (0:N-1) * Fs/N;
    X = abs(fft(x, N));
    subplot(length(N_values), 1, i);
    plot(f, X);
    xlabel('Frequency (Hz)');
    ylabel('Magnitude');
    title(['N = ' num2str(N)]);
end

第三题：

（1）计算周期

信号 x[n] 的周期可以通过求两个频率成分的最小公倍数来确定。

对于频率成分 0.48π 和 0.52π，它们的周期分别是 2π/0.48π ≈ 4.1667 和 2π/0.52π ≈ 3.8462。

要找到两个周期的最小公倍数，我们可以计算它们的倒数，然后取它们的最大公约数的倒数。

最小公倍数 = 1 / (最大公约数的倒数)

计算最大公约数的倒数：

1 / 4.1667 ≈ 0.24

1 / 3.8462 ≈ 0.26

计算最大公约数的倒数：

1 / (最大公约数的倒数) ≈ 1 / 0.02 = 50

因此，信号 x[n] 的周期为 50。

% 参数设置
N = 50; % 一个周期的信号长度
n = 0:N-1; % 时间轴
x = cos(0.48*pi*n) + cos(0.52*pi*n); % 一个周期的信号

% 计算一个周期的 DFT
X_periodic = fft(x);

% 补零并计算 DFT
x_padded = [x zeros(1, 100-N)]; % 补零
X_padded = fft(x_padded);

N100=100;
n100=0:N100-1;
x100=cos(0.48*pi*n100) + cos(0.52*pi*n100); 
% 取 0 ≤ n ≤ 99 并计算 DFT
x_truncated = x100; % 补零使得长度为 100
X_truncated = fft(x_truncated); % 不指定 DFT 点数，使用默认值

% 绘制幅频特性
figure;
subplot(3, 1, 1);
stem(abs(X_periodic));
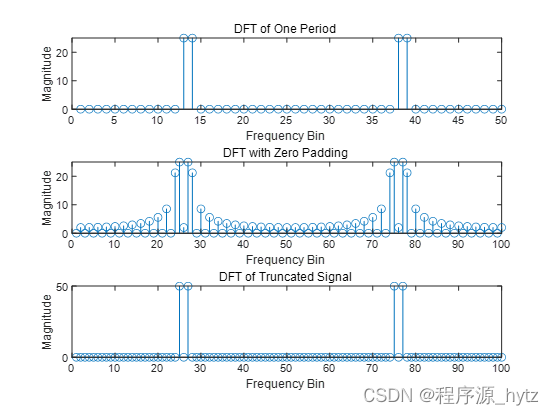
title('DFT of One Period');
xlabel('Frequency Bin');
ylabel('Magnitude');

subplot(3, 1, 2);
stem(abs(X_padded));
title('DFT with Zero Padding');
xlabel('Frequency Bin');
ylabel('Magnitude');

subplot(3, 1, 3);
stem(abs(X_truncated));
title('DFT of Truncated Signal');
xlabel('Frequency Bin');
ylabel('Magnitude');