文章目录
- 计算高可用
- 存储高可用
- 高可用状态决策
- 小结

今天,我们聊聊复杂度的第二个来源高可用。
参考维基百科,先来看看高可用的定义。
系统无中断地执行其功能的能力,代表系统的可用性程度,是进行系统设计时的准则之一。
这个定义的关键在于“无中断”,但恰好难点也在“无中断”上面,因为无论是单个硬件还是单个软件,都不可能做到无中断,硬件会出故障,软件会有 bug;硬件会逐渐老化,软件会越来越复杂和庞大……
除了硬件和软件本质上无法做到“无中断”,外部环境导致的不可用更加不可避免、不受控制。例如,断电、水灾、地震,这些事故或者灾难也会导致系统不可用,而且影响程度更加严重,更加难以预测和规避。
所以,系统的高可用方案五花八门,但万变不离其宗,本质上都是通过“冗余”来实现高可用。通俗点来讲,就是一台机器不够就两台,两台不够就四台;一个机房可能断电,那就部署两个机房;一条通道可能故障,那就用两条,两条不够那就用三条(移动、电信、联通一起上)。高可用的“冗余”解决方案,单纯从形式上来看,和之前讲的高性能是一样的,都是通过增加更多机器来达到目的,但其实本质上是有根本区别的:高性能增加机器目的在于“扩展”处理性能;高可用增加机器目的在于“冗余”处理单元。
通过冗余增强了可用性,但同时也带来了复杂性,我会根据不同的应用场景逐一分析。
计算高可用
这里的“计算”指的是业务的逻辑处理。计算有一个特点就是无论在哪台机器上进行计算,同样的算法和输入数据,产出的结果都是一样的,所以将计算从一台机器迁移到另外一台机器,对业务并没有什么影响。既然如此,计算高可用的复杂度体现在哪里呢?最简单的单机变双机为例进行分析。先来看一个单机变双机的简单架构示意图。
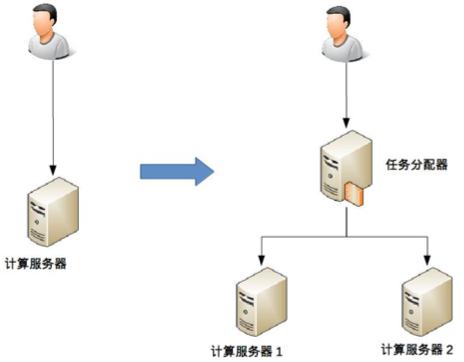
你可能会发现,这个双机的架构图和上期“高性能”讲到的双机架构图是一样的,因此复杂度也是类似的,具体表现为:
- 需要增加一个任务分配器,选择合适的任务分配器也是一件复杂的事情,需要综合考虑性能、成本、可维护性、可用性等各方面因素。
- 任务分配器和真正的业务服务器之间有连接和交互,需要选择合适的连接方式,并且对连接进行管理。例如,连接建立、连接检测、连接中断后如何处理等。
- 任务分配器需要增加分配算法。例如,常见的双机算法有主备、主主,主备方案又可以细分为冷备、温备、热备。
上面这个示意图只是简单的双机架构,我们再看一个复杂一点的高可用集群架构。
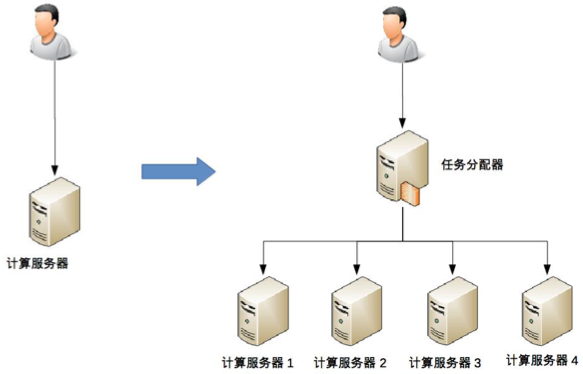
这个高可用集群相比双机来说,分配算法更加复杂,可以是 1 主 3 备、2 主 2 备、3 主 1 备、4 主 0 备,具体应该采用哪种方式,需要结合实际业务需求来分析和判断,并不存在某种算法就一定优于另外的算法。例如,ZooKeeper 采用的就是 1 主多备,而 Memcached 采用的就是全主 0 备。
存储高可用
对于需要存储数据的系统来说,整个系统的高可用设计关键点和难点就在于“存储高可用”。存储与计算相比,有一个本质上的区别:将数据从一台机器搬到到另一台机器,需要经过线路进行传输。线路传输的速度是毫秒级别,同一机房内部能够做到几毫秒;分布在不同地方的机房,传输耗时需要几十甚至上百毫秒。例如,从广州机房到北京机房,稳定情况下 ping 延时大约是 50ms,不稳定情况下可能达到 1s 甚至更多。
虽然毫秒对于人来说几乎没有什么感觉,但是对于高可用系统来说,就是本质上的不同,这意味着整个系统在某个时间点上,数据肯定是不一致的。按照“数据 + 逻辑 = 业务”这个公式来套的话,数据不一致,即使逻辑一致,最后的业务表现就不一样了。以最经典的银行储蓄业务为例,假设用户的数据存在北京机房,用户存入了 1 万块钱,然后他查询的时候被路由到了上海机房,北京机房的数据没有同步到上海机房,用户会发现他的余额并没有增加 1 万块。想象一下,此时用户肯定会背后一凉,马上会怀疑自己的钱被盗了,然后赶紧打客服电话投诉,甚至打 110 报警,即使最后发现只是因为传输延迟导致的问题,站在用户的角度来说,这个过程的体验肯定很不好。
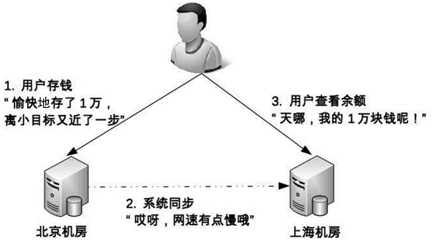
除了物理上的传输速度限制,传输线路本身也存在可用性问题,传输线路可能中断、可能拥塞、可能异常(错包、丢包),并且传输线路的故障时间一般都特别长,短的十几分钟,长的几个小时都是可能的。例如,2015 年支付宝因为光缆被挖断,业务影响超过 4 个小时;2016 年中美海底光缆中断 3 小时等。在传输线路中断的情况下,就意味着存储无法进行同步,在这段时间内整个系统的数据是不一致的。
综合分析,无论是正常情况下的传输延迟,还是异常情况下的传输中断,都会导致系统的数据在某个时间点或者时间段是不一致的,而数据的不一致又会导致业务问题;但如果完全不做冗余,系统的整体高可用又无法保证,所以存储高可用的难点不在于如何备份数据,而在于如何减少或者规避数据不一致对业务造成的影响。
分布式领域里面有一个著名的 CAP 定理,从理论上论证了存储高可用的复杂度。也就是说,存储高可用不可能同时满足“一致性、可用性、分区容错性”,最多满足其中两个,这就要求我们在做架构设计时结合业务进行取舍。
高可用状态决策
无论是计算高可用还是存储高可用,其基础都是“状态决策”,即系统需要能够判断当前的状态是正常还是异常,如果出现了异常就要采取行动来保证高可用。如果状态决策本身都是有错误或者有偏差的,那么后续的任何行动和处理无论多么完美也都没有意义和价值。但在具体实践的过程中,恰好存在一个本质的矛盾:通过冗余来实现的高可用系统,状态决策本质上就不可能做到完全正确。下面我基于几种常见的决策方式进行详细分析。
- 独裁式
独裁式决策指的是存在一个独立的决策主体,我们姑且称它为“决策者”,负责收集信息然后进行决策;所有冗余的个体,我们姑且称它为“上报者”,都将状态信息发送给决策者。
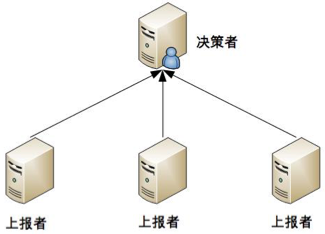
独裁式的决策方式不会出现决策混乱的问题,因为只有一个决策者,但问题也正是在于只有一个决策者。当决策者本身故障时,整个系统就无法实现准确的状态决策。如果决策者本身又做一套状态决策,那就陷入一个递归的死循环了。
- 协商式
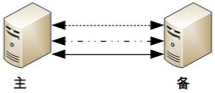
协商式决策指的是两个独立的个体通过交流信息,然后根据规则进行决策,最常用的协商式决策就是主备决策。
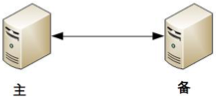
这个架构的基本协商规则可以设计成:
- 2 台服务器启动时都是备机。
- 2 台服务器建立连接。
- 2 台服务器交换状态信息。
- 某 1 台服务器做出决策,成为主机;另一台服务器继续保持备机身份。
协商式决策的架构不复杂,规则也不复杂,其难点在于,如果两者的信息交换出现问题(比如主备连接中断),此时状态决策应该怎么做。
- 如果备机在连接中断的情况下认为主机故障,那么备机需要升级为主机,但实际上此时主机并没有故障,那么系统就出现了两个主机,这与设计初衷(1 主 1 备)是不符合的。
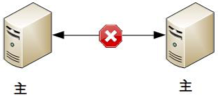
- 如果备机在连接中断的情况下不认为主机故障,则此时如果主机真的发生故障,那么系统就没有主机了,这同样与设计初衷(1 主 1 备)是不符合的。
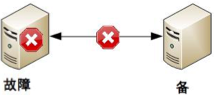
- 如果为了规避连接中断对状态决策带来的影响,可以增加更多的连接。例如,双连接、三连接。这样虽然能够降低连接中断对状态带来的影响(注意:只能降低,不能彻底解决),但同时又引入了这几条连接之间信息取舍的问题,即如果不同连接传递的信息不同,应该以哪个连接为准?实际上这也是一个无解的答案,无论以哪个连接为准,在特定场景下都可能存在问题。
综合分析,协商式状态决策在某些场景总是存在一些问题的。
- 民主式
民主式决策指的是多个独立的个体通过投票的方式来进行状态决策。例如,ZooKeeper 集群在选举 leader 时就是采用这种方式。
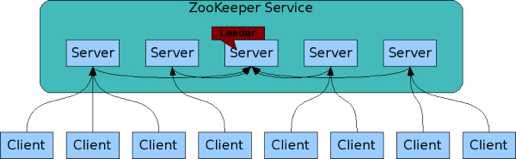
民主式决策和协商式决策比较类似,其基础都是独立的个体之间交换信息,每个个体做出自己的决策,然后按照“多数取胜”的规则来确定最终的状态。不同点在于民主式决策比协商式决策要复杂得多,ZooKeeper 的选举算法 Paxos,绝大部分人都看得云里雾里,更不用说用代码来实现这套算法了。
除了算法复杂,民主式决策还有一个固有的缺陷:脑裂。这个词来源于医学,指人体左右大脑半球的连接被切断后,左右脑因为无法交换信息,导致各自做出决策,然后身体受到两个大脑分别控制,会做出各种奇怪的动作。例如:当一个脑裂患者更衣时,他有时会一只手将裤子拉起,另一只手却将裤子往下脱。脑裂的根本原因是,原来统一的集群因为连接中断,造成了两个独立分隔的子集群,每个子集群单独进行选举,于是选出了 2 个主机,相当于人体有两个大脑了。
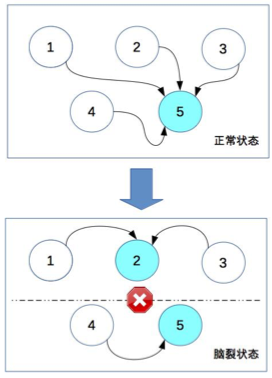
从图中可以看到,正常状态的时候,节点 5 作为主节点,其他节点作为备节点;当连接发生故障时,节点 1、节点 2、节点 3 形成了一个子集群,节点 4、节点 5 形成了另外一个子集群,这两个子集群的连接已经中断,无法进行信息交换。按照民主决策的规则和算法,两个子集群分别选出了节点 2 和节点 5 作为主节点,此时整个系统就出现了两个主节点。这个状态违背了系统设计的初衷,两个主节点会各自做出自己的决策,整个系统的状态就混乱了。
为了解决脑裂问题,民主式决策的系统一般都采用“投票节点数必须超过系统总节点数一半”规则来处理。如图中那种情况,节点 4 和节点 5 形成的子集群总节点数只有 2 个,没有达到总节点数 5 个的一半,因此这个子集群不会进行选举。这种方式虽然解决了脑裂问题,但同时降低了系统整体的可用性,即如果系统不是因为脑裂问题导致投票节点数过少,而真的是因为节点故障(例如,节点 1、节点 2、节点 3 真的发生了故障),此时系统也不会选出主节点,整个系统就相当于宕机了,尽管此时还有节点 4 和节点 5 是正常的。
综合分析,无论采取什么样的方案,状态决策都不可能做到任何场景下都没有问题,但完全不做高可用方案又会产生更大的问题,如何选取适合系统的高可用方案,也是一个复杂的分析、判断和选择的过程。
小结
今天我们聊了复杂度来源之一的高可用,分析了计算高可用和存储高可用两个场景,给出了几种高可用状态决策方式,希望对你有所帮助。
【星猿杂谈】:在这里我们共同探索科技新趋势,分享积累的点滴,从编程语言到系统架构,从人工智能到高性能计算,我们追求技术的进步,同时珍视分享的力量。欢迎关注我们,在技术的精彩世界中一起遨游,发现更多未知!


![[网络编程]UDP协议,基于UDP协议的回显服务器](https://img-blog.csdnimg.cn/direct/e369e33746cd4867bc532f82b2e9577c.png)