Key Concept
蒙特卡罗方法(Monte Carlo Method),也称为统计模拟方法,是一种基于概率和统计的数值计算方法。该方法使用随机数(或更常见的伪随机数)来解决可能非常复杂的数学或物理问题。蒙特卡罗方法广泛应用于金融、物理、工程、运筹学等领域。
建模思路
-
定义问题的概率模型:
- 确定问题的数学或物理模型,并将其转化为可以通过概率方法解决的形式。
-
生成随机数:
- 根据问题的概率分布生成随机数或伪随机数序列。
-
进行模拟实验:
- 利用随机数进行大量模拟实验或计算,得到问题的近似解。
-
收集结果并分析:
- 收集和记录每次模拟实验的结果,对这些数据进行统计分析。
-
结果的估计和验证:
- 通过模拟实验结果的分析得到问题的统计特性,如均值、方差等,并据此估计问题的解。
- 可以通过多次模拟实验来提高结果的准确度。
-
误差估计:
- 评估模拟结果的误差范围,通常误差与模拟次数的平方根成反比。
示例
1.模拟求解圆周率
用随机投掷的点数来模拟计算圆周率
#使用蒙特卡罗方法近似求解圆周率
import random
import math
import time
#这里我们设置圆的半径为1,那么圆的面积就是pi
#而正方形的面积就是4
#那么圆的面积和正方形的面积的比值就是pi/4
#我们可以随机产生一些点,然后判断这些点是否在圆内
#如果在圆内,那么就计数,计数的值和总数的比值就是S(圆)/S(正方形)=pi*r^2/4r^2=pi/4 =》 pi = 4*S(圆)/S(正方形) =》 pi = 4*hits/DARTS
DARTS = 100000000#抛洒点的总数
hits = 0.0
start = time.perf_counter()#计时开始
for i in range(1, DARTS+1):
x, y = random.random(), random.random()#随机产生一个0~1的浮点数
dist = math.sqrt(x**2 + y**2)#计算点到圆心的距离
#判断点是否在圆内
if dist <= 1.0:
hits += 1
pi = 4 * (hits/DARTS)
print("Pi的值是:{}".format(pi))
2.模拟三门问题
蒙提霍尔问题(英文:Monty Hall problem),亦称为蒙特霍问题、山羊问题或三门问题,是一个源自博弈论的数学游戏问题,参赛者会看见三扇门,其中一扇门的里面有一辆汽车,选中里面是汽车的那扇门,就可以赢得该辆汽车,另外两扇门里面则都是一只山羊。当参赛者选定了一扇门,主持人会开启另一扇是山羊的门;并问:“要不要换一扇门?”依照玛丽莲·沃斯·莎凡特的见解,参赛者应该换,换门的话,赢得汽车的概率是2/3。这问题亦被叫做蒙提霍尔悖论:因为该问题的答案虽在逻辑上并无矛盾,但十分违反直觉。
蒙提霍尔问题得名于主持人蒙蒂·霍尔,他主持美国的电视游戏节目《Let's Make a Deal》时,会有这样的游戏,他也确实会先开启另一扇是山羊的门,来吸引观众眼球;但他不会允许参赛者换门。蒙提霍尔问题首次出现,可能是在1889年约瑟夫·贝特朗所著的Calcul des probabilités一书中。在这本书中,这条问题被称为“贝特朗箱子悖论”(Bertrand's Box Paradox)。另一种形式则是三囚问题(Three prisoners problem),原理是一模一样的,1959年出现在马丁·加德纳的《数学游戏》专栏中,其后被改编成各种语言的版本。
某校某系概率论期中考试题
#用蒙特卡洛方法求解三门问题
import random
def hall(simulation,change_door):
win_count=0
for i in range(simulation):
prize_door=random.randint(0,2)
choice_door=random.randint(0,2)
host=[i for i in range(3) if i!=choice_door and i!=prize_door][0]
if change_door:
choice_door=[i for i in range(3) if i!=choice_door and i!=host][0]
if choice_door==prize_door:
win_count+=1
return win_count/simulation
simulation=1000000
change_rate=hall(simulation,True)
no_change_rate=hall(simulation,False)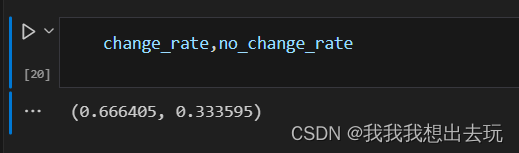
这里看出一定要换门..........
这个问题实在是反人类直觉,贝叶斯公式也能推导这个问题的