文章目录
- 1. 前言
- 2. 算法题
- 1046.最后一块石头的重量
- 703.数据流中的第K大元素
- 2.5 如何选择大根堆 与 小根堆? + 为什么选择大根堆(小根堆)?
- 692.前K个高频单词
- 295.数据流的中位数
1. 前言
我们知道:优先级队列是一种常用的数据结构,用于解决许多算法问题。基于堆(Heap)实现,在每次操作中能够快速找到最大或最小值。
使用优先级队列的典型算法问题包括:
- Top K 问题:查找列表中前 K 个最大或最小的元素。
- 合并 K 个排序数组:将 K 个已排序的数组合并为一个有序数组。
- Dijkstra 算法:在加权图中找到从起点到目标节点的最短路径。
- Huffman 编码:使用最小堆构建前缀编码树来压缩数据。
下面会挑选一些算法题并使用优先级队列进行解题。
2. 算法题
1046.最后一块石头的重量

思路
- 解法:大根堆
- 大根堆:每个节点都大于等于其子节点,则堆顶节点为最大的
- 将数组中所有元素加入堆中,并进行循环,直至堆为空
- 循环每次 取两次堆顶元素,即当前最重的两石头
- 将两元素差继续入堆,重复过程直至循环结束
- 如果堆中还剩一个元素,返回该元素
- 如果已经没有元素,返回0
代码
int lastStoneWeight(vector<int>& stones) {
priority_queue<int> heap; // 创建大根堆
// 将数组所有元素添加到堆中
for(int stone : stones) heap.push(stone);
while(heap.size() > 1)
{
// 每次取最大的两个数
int a = heap.top(); heap.pop();
int b = heap.top(); heap.pop();
if(a > b) heap.push(a - b);
}
return heap.size() ? heap.top() : 0;
}
703.数据流中的第K大元素

思路
- 题意分析:根据题目,可以看出来该题是一道topK类型题
- 解法:全局变量 + 小根堆
- 使用全局变量可以省去函数之间传参的过程,也方便编写代码
- 创建全局变量标记k和创建全局小根堆
- 关于为什么选择小根堆,可以看后面的解释。
- 由于add函数要求添加数字后返回第k大的元素,对于构造函数KthLargest,我们直接将数组中前k大的元素插入
- 对于add函数,直接将val插入到堆中并判断是否堆内元素超出k个
- 如果超出,则pop掉,后直接返回堆顶元素(即为第K大)
2.5 如何选择大根堆 与 小根堆? + 为什么选择大根堆(小根堆)?

代码
class KthLargest {
public:
// 小根堆
priority_queue<int, vector<int>, greater<int>> heap;
int _k;
KthLargest(int k, vector<int>& nums) {
_k = k;
for(int num : nums){
heap.push(num);
if(heap.size() > _k) heap.pop();
}
}
int add(int val) {
heap.push(val);
if(heap.size() > _k) heap.pop();
return heap.top();
}
};
692.前K个高频单词

思路
- 题意分析:即返回数组中出现次数最多的字符串(单词)
- 解法:哈希表 + 优先级队列
- 哈希表统计每个单词的出现次数
- 根据题目要求,当单词的频率相同时,按照字典序排列,则我们自定义优先级队列的比较函数。则:
- 当单词频率不同时,用小堆的比较方式
- 当单词频率相同时,按照字典序,用大堆的比较方式
- 将哈希表中统计的前k高的 字母以及频率 加入到队列
- 最后返回结果,遍历堆,每次加入到结果集result中并pop即可。
代码
vector<string> topKFrequent(vector<string>& words, int k) {
// 统计单词出现频率
unordered_map<string, int> freq;
for (const string& word : words) {
freq[word]++;
}
// 自定义优先队列的比较函数
auto cmp = [](const pair<string, int>& a, const pair<string, int>& b) {
// 比较出现次数,如果相同则按照字母顺序
return a.second > b.second || (a.second == b.second && a.first < b.first);
};
// 优先队列,默认是大顶堆,用于存储频率最高的 k 个单词
priority_queue<pair<string, int>, vector<pair<string, int>>, decltype(cmp)> pq(cmp);
// 遍历统计好的频率,将单词加入优先队列
for (const auto& entry : freq) {
pq.push(entry);
if (pq.size() > k) {
pq.pop(); // 如果队列大小超过 k,则弹出频率最小的单词
}
}
// 从优先队列中取出结果
vector<string> result(k);
for (int i = k - 1; i >= 0; --i) {
result[i] = pq.top().first; // 逆序存储结果
pq.pop();
}
return result;
}
295.数据流的中位数

思路
-
题意分析:题目要求实现一个类,类中包含一个构造函数、一个add函数用于添加元素、以及一个find函数
-
解法一:排序 sort

- 对于本题,使用该排序法是会超时的
-
解法二:插入排序的思想
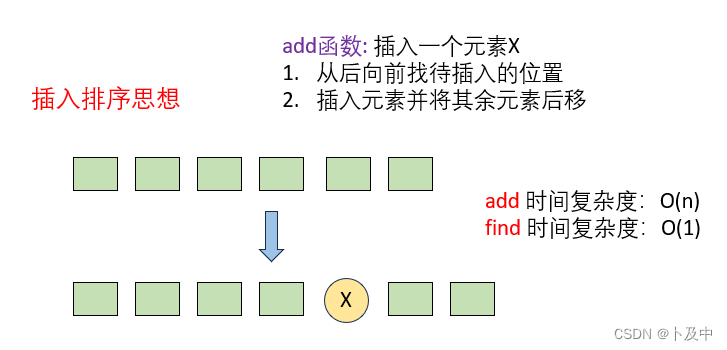
- 插入排序思想解本题是有可能超时的,但依然需要了解这种解题思想。
-
解法三:大小堆维护
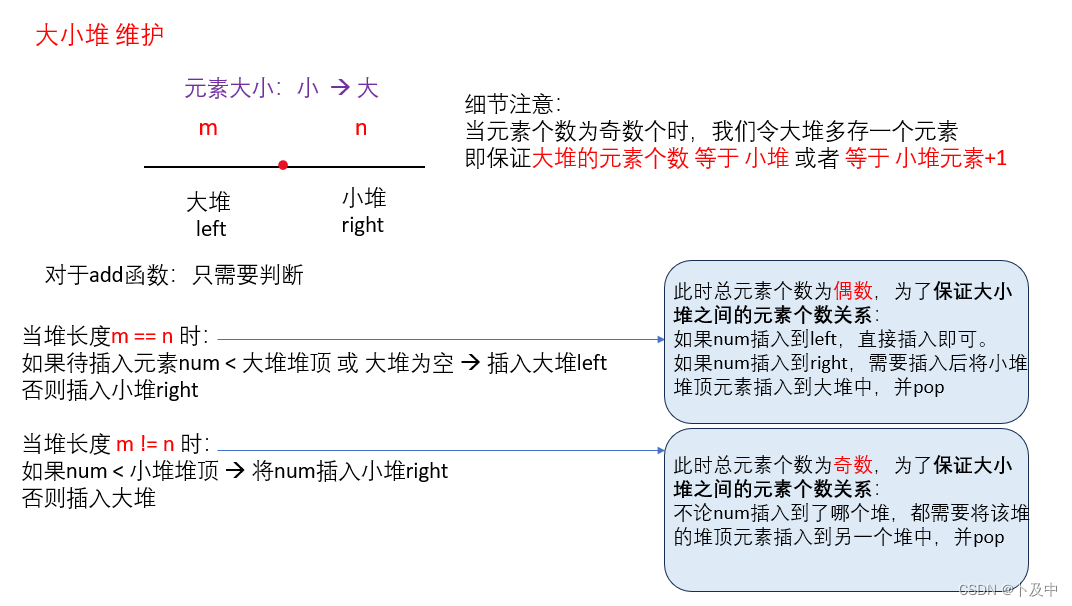
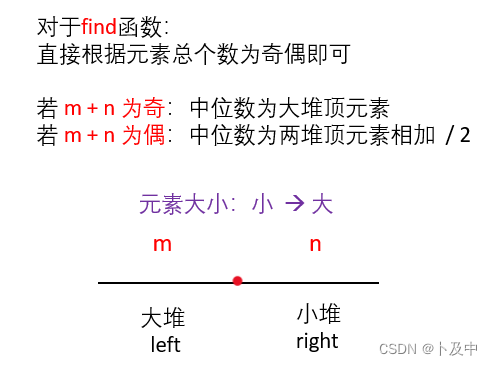
- 上图解释了方法思路,具体细节看下面代码即可。
代码
class MedianFinder {
public:
// 大小堆,左大堆,右小堆
// 且当共有奇数个元素时,左存多一个元素
priority_queue<int, vector<int>> left;
priority_queue<int, vector<int>, greater<int>> right;
MedianFinder() {} // 构造
void addNum(int num) {
if(left.size() == right.size())
{
if(left.empty() || num <= left.top())
{
left.push(num);
}
else
{
right.push(num);
left.push(right.top());
right.pop();
}
}
else
{
if(num <= left.top())
{
left.push(num);
right.push(left.top());
left.pop();
}
else
{
right.push(num);
}
}
}
double findMedian() {
return (left.size() == right.size()) ? (left.top() + right.top()) / 2.0 : left.top();
}
};