1. 概述
在本教程中,我们将研究卷积神经网络背后的理论及其架构。
我们将首先讨论通常使用卷积神经网络 (CNN) 执行的任务和特征提取问题。然后,我们将讨论为什么需要CNN,以及为什么传统的前馈神经网络是不够的。
然后,我们将在矩阵运算的上下文中讨论卷积的操作。这将使我们很好地理解卷积神经网络的运行机制。
最后,我们将讨论卷积层以外的卷积神经网络的特征,重点是池化和辍学。
在本教程结束时,我们将知道什么是卷积神经网络以及它解决了哪些问题。
2. 我们什么时候使用CNN
2.1. 为什么图像识别如此困难?
CNN用于解决一类特定的问题,其中包括提取和识别数据集中的抽象特征。让我们通过一个简单的例子看看这在实践中意味着什么:

我们可以看到,上图中包含的所有图像都代表了不同形状、大小和颜色的苹果。人类不难将它们识别为苹果,尽管它们略有不同。但是,对于计算机来说,这些图像似乎彼此完全不同:
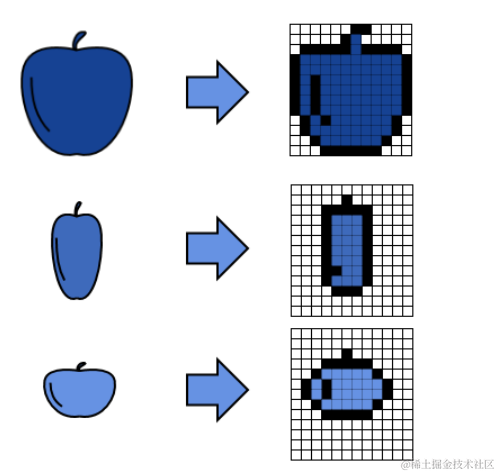
这些图像,无论它们看起来多么相似,但对计算机来说几乎没有共同点。这是因为对人类来说,它似乎是一个明确定义的对象,对计算机来说只是数字的集合。人类感知系统实际上使用上下文线索来识别对象,但不幸的是,计算机无法使用这些线索。
这意味着计算机需要完全依赖数据来执行诸如识别图像中的物体之类的任务。然而,这些数据可能会有很大差异,正如我们在上面的示例图像中看到的那样。那么,我们如何才能构建一个能够处理变化如此之大的数据的系统呢?
2.2. 解决方案是抽象
识别苹果的任务变得困难,因为太多的像素可以承担太多的值。然而,它们中的每一个都单独携带很少的信息。这意味着图像是高度熵的,除非我们以某种方式显着降低这种熵,否则我们无法使用它。
但是,如果我们有一种方法来学习输入的抽象特征,这反过来又会使分类变得明显更容易。让我们想象一下,我们可以将苹果描述为一个有茎的物体,加上足够平坦的底部,当然还有一个圆形:
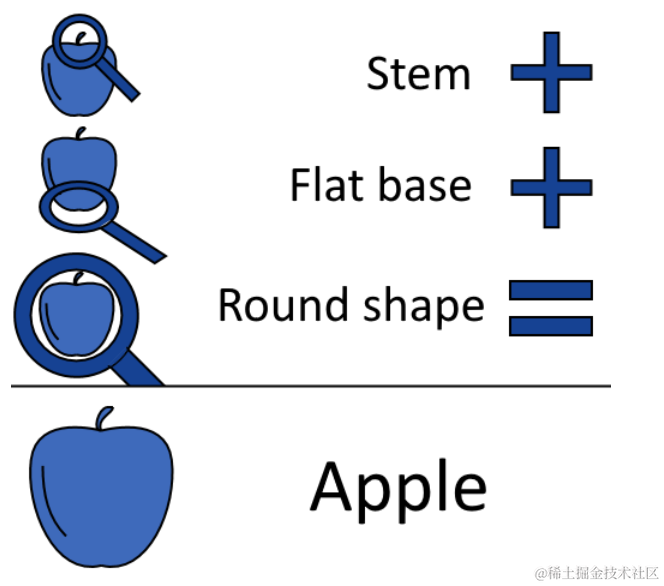
如果我们可以在分类算法中对这些特征进行编码,这将反过来使看不见的图像的分类更容易。在这种情况下,我们可以创建一个模型来编码我们正在寻找的特征,并将拥有所有这些特征的图像归类为“苹果”:
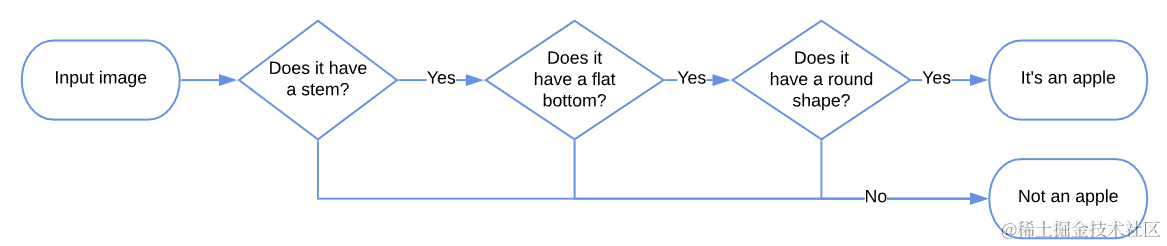
卷积神经网络以这种方式工作;只有,他们才能自动学习这些功能。事实上,它们是一种通过算法学习数据集抽象表示的方法。这反过来又促进了分类任务,并有助于解决所谓的维度诅咒,正如我们稍后将看到的那样。
3. 神经网络及其诅咒
3.1. CNN解决的问题
根据我们关于机器学习相关主题的介绍性文章的传统,我们还将开始研究卷积神经网络(以下简称 CNN),对嵌入在此机器学习模型中的先验或隐式知识进行少量分析。最好的解释是问自己一个问题:
- “我们为什么不简单地使用前馈神经网络进行图像分类呢?”
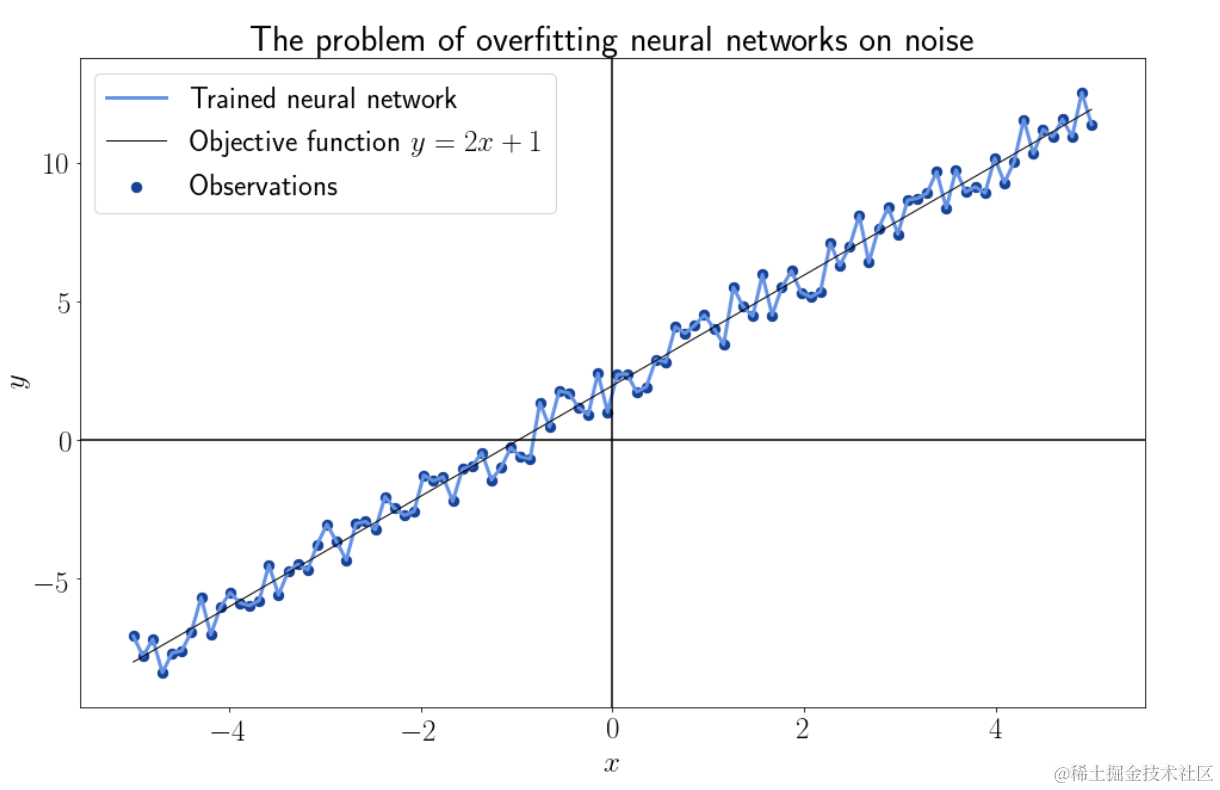
事实上,我们知道前馈神经网络可以近似于形式 的任何连续函数。然而不能保证神经网络可以学习该功能。作为一般规则,如果我们有疑问,可以安全地假设神经网络会过度拟合其训练数据的噪声,并且永远不会学习任何给定的目标函数:
的任何连续函数。然而不能保证神经网络可以学习该功能。作为一般规则,如果我们有疑问,可以安全地假设神经网络会过度拟合其训练数据的噪声,并且永远不会学习任何给定的目标函数:
3.2. 卷积和正则化
减少数据集中用于神经网络训练的噪声的尝试被称为正则化。卷积是一种特殊类型的正则化,它利用特征或观测值的线性依赖性。反过来,这让我们可以减少噪声并恢复与先前关于特征线性独立性的假设的一致性,正如我们稍后将看到的那样。
从广义上讲,正则化包括将数据集的特征映射到具有较低熵的新特征。在形式上,这意味着我们变换特征 ,使得如果
,使得如果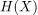 是熵
是熵 ,那么。这让我们学习一个新的目标函数,它不太容易受到过拟合的影响:
,那么。这让我们学习一个新的目标函数,它不太容易受到过拟合的影响:

卷积本质上是通过用更复杂的版本替换观测中的高熵特征来执行这项任务。这是由于某些类别的数据系统地违反了使用神经网络的一个重要先决条件,即特征的线性独立性这一事实成为可能。
3.3. 特征的线性(非)依赖性
现在让我们更详细地了解特征线性独立的含义。我们可以通过一个例子来做到这一点,方法是将两个变量X分布的建模扩展到第三维Y,如上所述。
对于这个例子,我们想象两个变量之间存在线性关系,使得一个变量可以用形式y=f(x)的函数近似另一个变量。特别是,我们假设这个函数具有任意选择参数的形式Y=2X+1。因此,我们可以说,通过构造,这两个变量是线性依赖的。
现在让我们看看如果我们使用两个线性因变量作为某个目标函数Z=g(X,Y)的输入会发生什么。下面的动画显示了从表单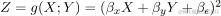 的目标函数采样的训练数据:
的目标函数采样的训练数据:

3.4. 将依赖特征转换为独立特征
对于图像中显示的特定分布,我们分配了值 ,但这仅用于说明目的。
,但这仅用于说明目的。
关于我们将用于回归的模型的结构,我们可以先验地预测它的一些特征。我们知道目标函数具有二次形式,因为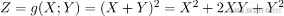 。由于Y是线性依赖
。由于Y是线性依赖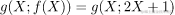 的。我们现在可以想象对这个函数执行多项式回归,以便学习它的参数。如果我们不用它的等价物f(X)替换Y,那么我们必须学习模型的五个参数:
的。我们现在可以想象对这个函数执行多项式回归,以便学习它的参数。如果我们不用它的等价物f(X)替换Y,那么我们必须学习模型的五个参数: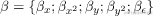 但是,由于这两个特征XY不是线性独立的,因此它们的线性组合也不是线性独立的。
但是,由于这两个特征XY不是线性独立的,因此它们的线性组合也不是线性独立的。
这意味着,我们可以学习一组对应于它们的线性组合的参数Y,而不是学习两个输入变量X的参数。因此,我们可以学习包含参 的更简单的模型。这在代数上对应于学习函数在投影向量空间
的更简单的模型。这在代数上对应于学习函数在投影向量空间 上的表示:
上的表示:

正如我们所看到的,在这个特定示例中,我们不需要两个输入特征,只需要一个。这是因为我们事先了解对输入特征的线性依赖性。反过来,这种先验知识使我们能够减少模型输入的维数及其参数,而不会通过代数变换损失任何代表性。
3.5. 维度的诅咒
这意味着,如果我们有充分的理由相信模型的输入特征不是线性独立的,我们可以减少模型所需的参数数量。这是通过利用我们的先验知识来完成的,即某些类别的数据(但不是全部)具有同时具有高维且彼此线性依赖的特征。
通常用CNN处理的数据通常具有高度的线性依赖性。最常见的示例是文本、音频、图像和视频信号:
- 对于文本数据,特征通常是单词,每个特征都在很大程度上取决于它之前和之后的特征
- 对于音频,频率大部分时间都在连续变化
- 相反,图像是对应于颜色的像素集合,其中每种颜色在大多数情况下都与其周围的一个像素相同
- 视频是一系列图像,如果它们包含真实世界的信息,这些图像只会由于对象的持久性而部分更改。
所有这些类型的数据都适合用CNN处理,以降低其维数。具有我们认为线性独立的特征的数据,例如关于引擎特征的数据集,并不适合CNN。
3.6. CNN的优势
通过在高维数据上使用CNN,我们可以帮助解决神经网络中的维数诅咒。这个问题是指神经网络增加其参数大小的趋势明显快于其输入大小的增加。
在上面的例子中,我们注意到,对于多项式回归的特定问题,可以将所需的参数数量减少 40%。对于现实世界的问题,这种下降要高得多,这使得使用卷积等降维技术成为一种必要而不是选择。
4. 神经网络中的卷积
4.1. 卷积的数学定义
我们现在明白了,如果我们的数据是线性相关的,并且具有高维的特征,我们需要使用方法来降低它的熵。其中一种方法就是卷积,cnn的名字就是来源于卷积运算。
神经网络中的卷积公式需要对输入数据进行识别。这是通过首先将我们执行卷积的数据(比如图像)分配到维度为(x,y)的矩阵Ax,y来完成的。然后,我们定义一个核矩阵k,它的元素会影响我们从卷积中得到的结果类型,我们将在下一节中看到。
卷积运算定义为矩阵A中的一个元素及其所有局部邻域的值,乘以核矩阵k中相应的元素:
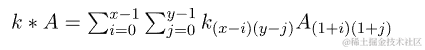
4.2. 卷积对矩阵的作用
现在让我们看看卷积在实际中对图像有什么作用。出于这个目的,我们将使用一个示例图像,看看如果我们改变核k,它会发生什么变化:

该图像由一个像素数组组成,我们可以通过首先定义一个核矩阵来应用卷积。存在各种内核,可用于不同的目的。在这里,我们将看到一些,从模糊的内核开始:
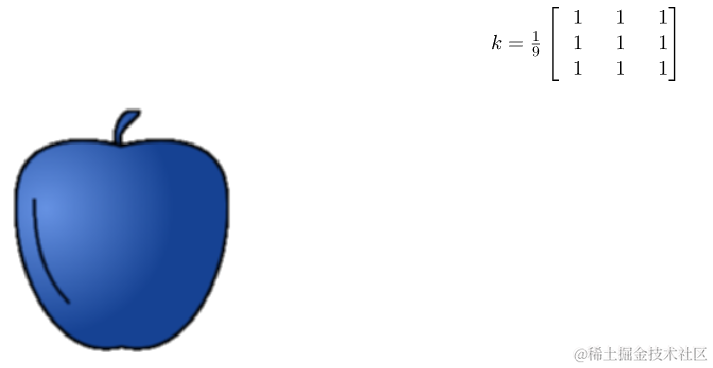
另一个内核是用于边缘检测的内核:
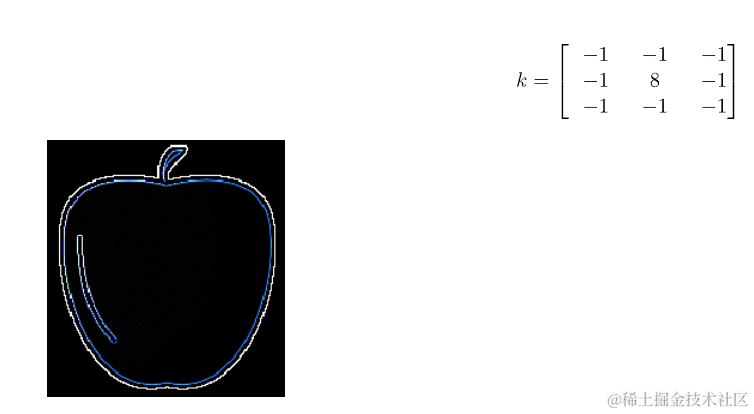
另一个是用于锐化功能的内核:

不同的卷积内核允许从相同的数据中提取不同的特征,这反过来又有助于CNN的训练。虽然卷积是CNN最典型的操作,架构本身就是从CNN得名的,但它并不是这个网络唯一独特的特征。
5. 卷积神经网络的其他特征
5.1. CNN 的一般架构
尽管被称为“卷积”神经网络,但CNN也具有一些与卷积无关的特殊特征。CNN与前馈神经网络区分开来的主要特征是:
- Pooling 层
- Dropout 层
- 还有一些特殊的激活功能
CNN 的典型架构通常包括一系列卷积层、池化层和辍学层,根据需要重复多次。然后,根据我们正在执行的任务,最后一层是分类或回归层。
让我们按顺序查看前两个的简短描述。我们可以参考我们的教程ReLU 作为 CNN 的激活函数来讨论最后一点。
5.2. 池化层
CNN的一个特殊特征是池化层,它进行池化的同名数学运算。池化包括从给定矩阵中提取具有较低维数的新矩阵,并且原始矩阵的每个聚类或邻域仅包含一个元素。最常见的池化方法是所谓的最大池化,其工作原理如下。
我们像以前一样采用矩阵Ax,y,它表示图像或其他输入数据。然后,我们将矩阵划分为固定大小的邻域。在本例中,我们选择了分布在池化窗口中的四个元素之间的(2,2)池化:

然后,我们确定给定邻域中最大的元素,并将其分配给我们为此目的创建的新矩阵:
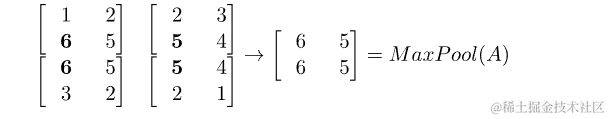
结果是一个新矩阵,仅由原始矩阵中邻居中的最大值组成。这会将输入数据的维度降低到使其更易于管理的水平,即使我们因此丢失了信息内容。然而,如上所述,输入要素的线性依赖性证明了这种权衡是合理的。
5.3. Dropout 层
卷积神经网络还实现了所谓的Dropout 层,将遗忘能力引入机器学习模型。这是基于这样一种观点,即关于某一现象的过多先前知识实际上可能阻碍而不是支持获得关于同一主题的未来知识。
辍学层通过随机停用给定层中的一些神经元来工作,从而迫使网络适应信息较少的信号进行学习。虽然违反直觉,但已经证明,当高阶交互是虚假的时,具有辍学层的卷积神经网络通常学习得更好。这是因为部分信号的无效有利于学习其抽象特征,这些特征在网络的更高层中表示。
对于给定的 dropout 参数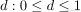 ,我们通过随机将值 0 分配给矩阵A的每个元素
,我们通过随机将值 0 分配给矩阵A的每个元素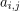 来获得 Dropout 函数的输出
来获得 Dropout 函数的输出 。如果
。如果
,那么形式就是: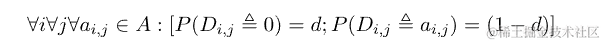
如果我们以上一节中的矩阵A为例,并且dropout的概率d = 0.4,我们可以得到这样的输出:

我们将在这个部分无效的矩阵上学习的模式对过拟合不太敏感。




![ElasticSearch扫盲概念篇[ES系列] - 第500篇](https://img-blog.csdnimg.cn/img_convert/aba21b37d7995dfb8a954ef15ed02eda.jpeg)