卷积神经网络（Convolutional Neural Networks）是一种深度学习模型或类似于人工神经网络的多层感知器，常用来分析视觉图像。

一.卷积神经网络基础概念

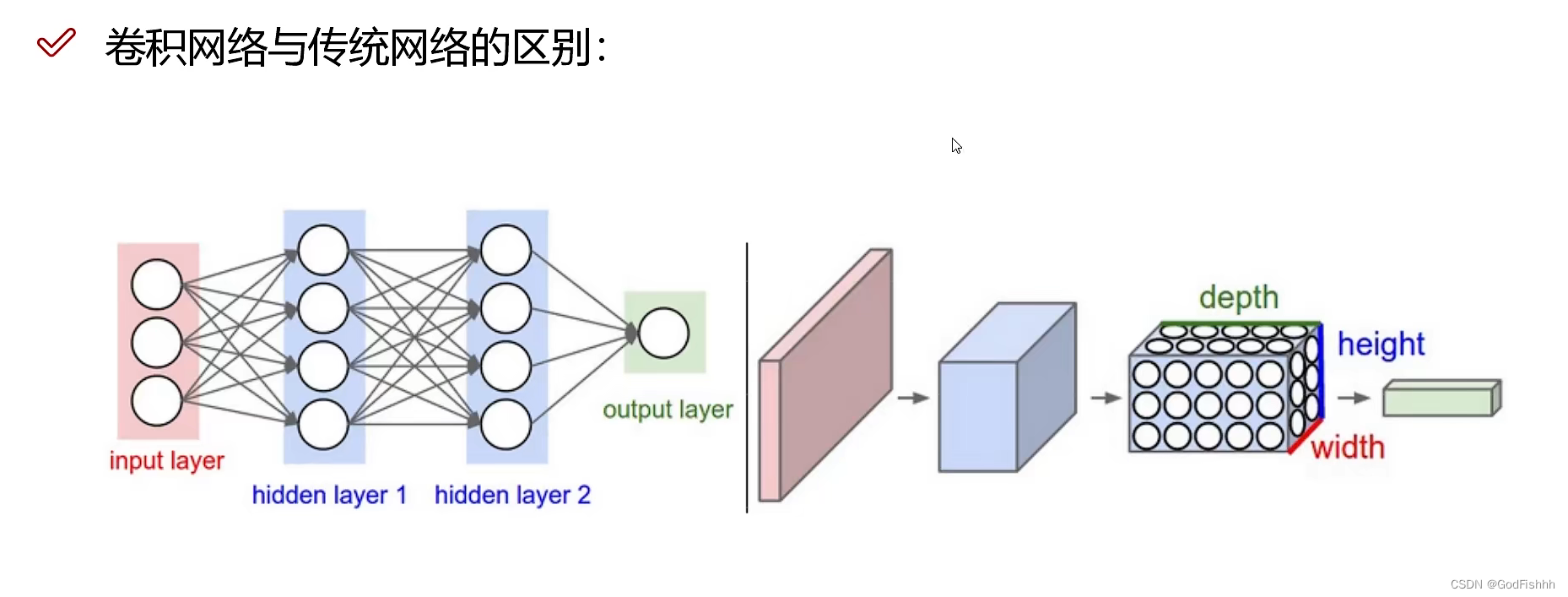
传统网络是二维的，而卷积网络是三维的。

例如32x32x3的图片，在传统网络中的输入是3072个像素点组合的矩阵，而在卷积网络中则是直接接受该特征图作为输入。

(1). 卷积是为了提取图像特征，通过卷积层，可以自动提取图像的高维度且有效的特征

(2). 池化主要是为了减少卷积层提取的特征个数，增加特征的鲁棒性或是为了降维

二.输入层 

数据输入层的主要目的是对原始图像数据进行预处理，其中包括：

1.去均值：把输入数据各个维度都中心化为0，如下图所示，其目的就是把样本的中心拉回到坐标系原点上。

2.归一化：幅度归一化到同样的范围，如下所示，即减少各维度数据取值范围的差异而带来的干扰，比如，我们有两个维度的特征A和B，A范围是0到10，而B范围是0到10000，如果直接使用这两个特征是有问题的，好的做法就是归一化，即A和B的数据都变为0到1的范围。

原图→去均值→归一化过程

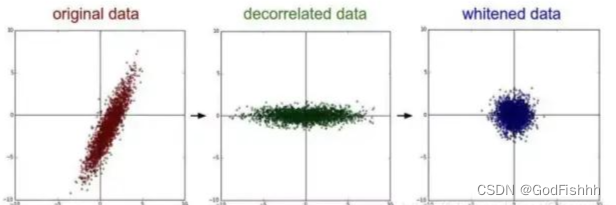
3.PCA/白化：用PCA降维；白化是对数据各个特征轴上的幅度归一化。

PCA降维参考资料:

【机器学习】降维——PCA（非常详细） - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/77151308原图→PCA降维→白化过程

三.卷积层

卷积的计算：

(1).左侧的三张图表示的是输入图片的三种颜色通道表示（eg.R,G,B），对应的卷积过程中使用的权重矩阵也需要有三种颜色通道（输入矩阵和权重矩阵的颜色通道参数应当相同） 。

(2).原始图像中选择的矩阵大小取决于Filter权重矩阵的大小，即取决于权重矩阵的前两个参数。

(3).同一个输入数据在不同的颜色通道中的像素点是不同的，对于每个颜色通道的数据需要设置不同的权重矩阵来进行过滤。

(4).输入矩阵和权重矩阵的计算通过内积来完成：即矩阵上的对应位置相乘然后再相加。

(5).通过权重矩阵过滤后得到的输出值应当是三个颜色通道分别计算出的过滤值相加再加上偏置值。

eg.如图对Input进行Filter W0计算，对于第一块选中的3x3的矩阵，Input的三个颜色通道矩阵和W0的三个颜色通道矩阵分别进行内积，得到的结果为0+2+0=2，再加上偏置值，此处设置为1，所以得到的Output矩阵中的第一个位置的值为2+1=3。

(6).每一个过滤器都能获得一个特征图，因此特征图的数量与过滤器的数量是相同的。

卷积层涉及参数：

(1).滑动窗口步长：选取的矩阵每次上下平移的单元格数量

(2).卷积核尺寸：即选择的卷积核的大小。

(3).边缘填充：边界的点对结果的影响较小，中间的点对结果的影响较大，为了使边界的点能够起到的作用更大，增加边缘填充（加一圈0，对结果没有影响），使原本边界的点能够利用的次数增多，对结果起到更大的作用。

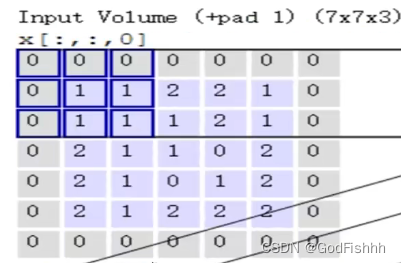
如图，原始矩阵应当是一个5x5x3的矩阵，通过+pad 1即增加一层边缘填充，扩大成一个7x7x3的矩阵。

(4).卷积核个数：与想要得到的特征图个数相同，每个卷积核的数据都是不同的。

卷积结果计算公式：

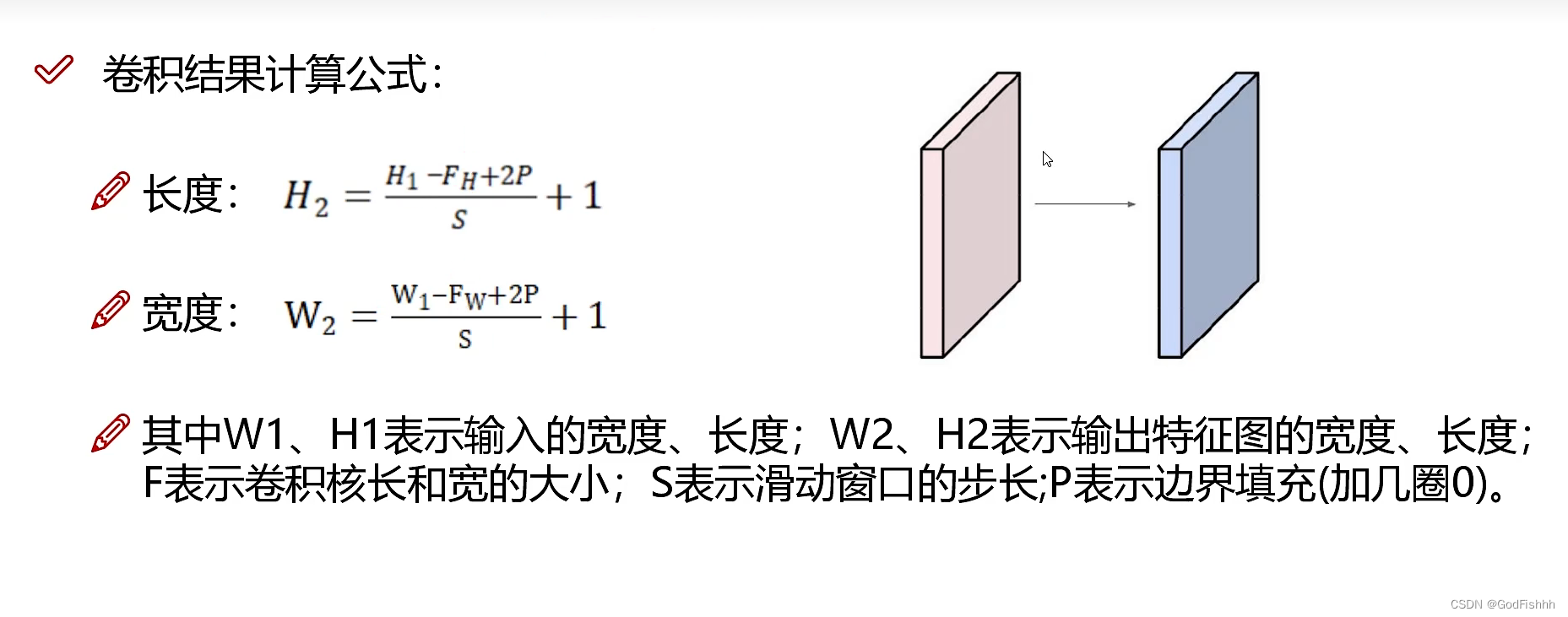
(1).通过卷积结果计算公式计算输出特征图的长度和宽度。

(2).输出特征图的深度和卷积核的个数相同。

四.池化层

池化层夹在连续的卷积层中间， 用于压缩数据和参数的量，减小过拟合。

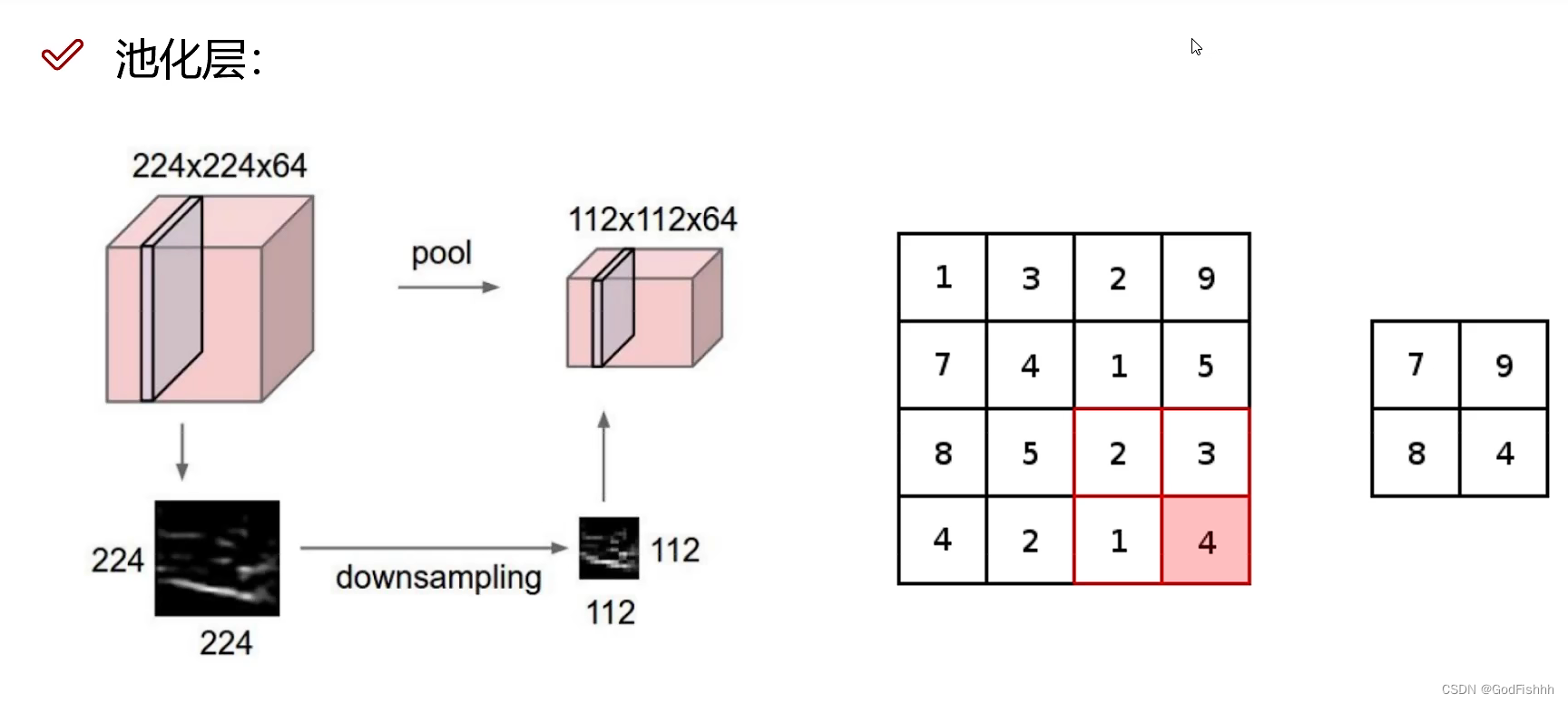
常用的池化方法：MAX POOLING

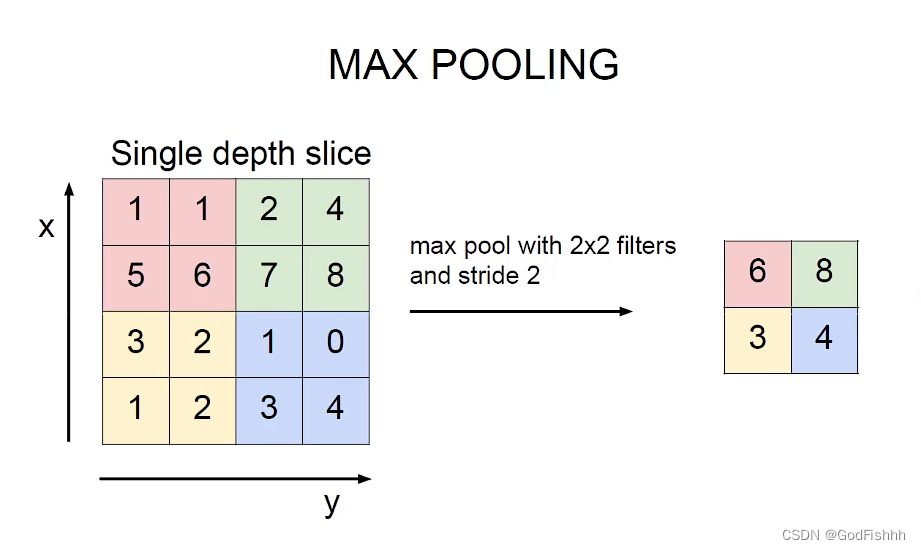 选择分块矩阵中最大的特征值作为压缩矩阵的值。(较大的特征值更加重要）

五.整体网络架构

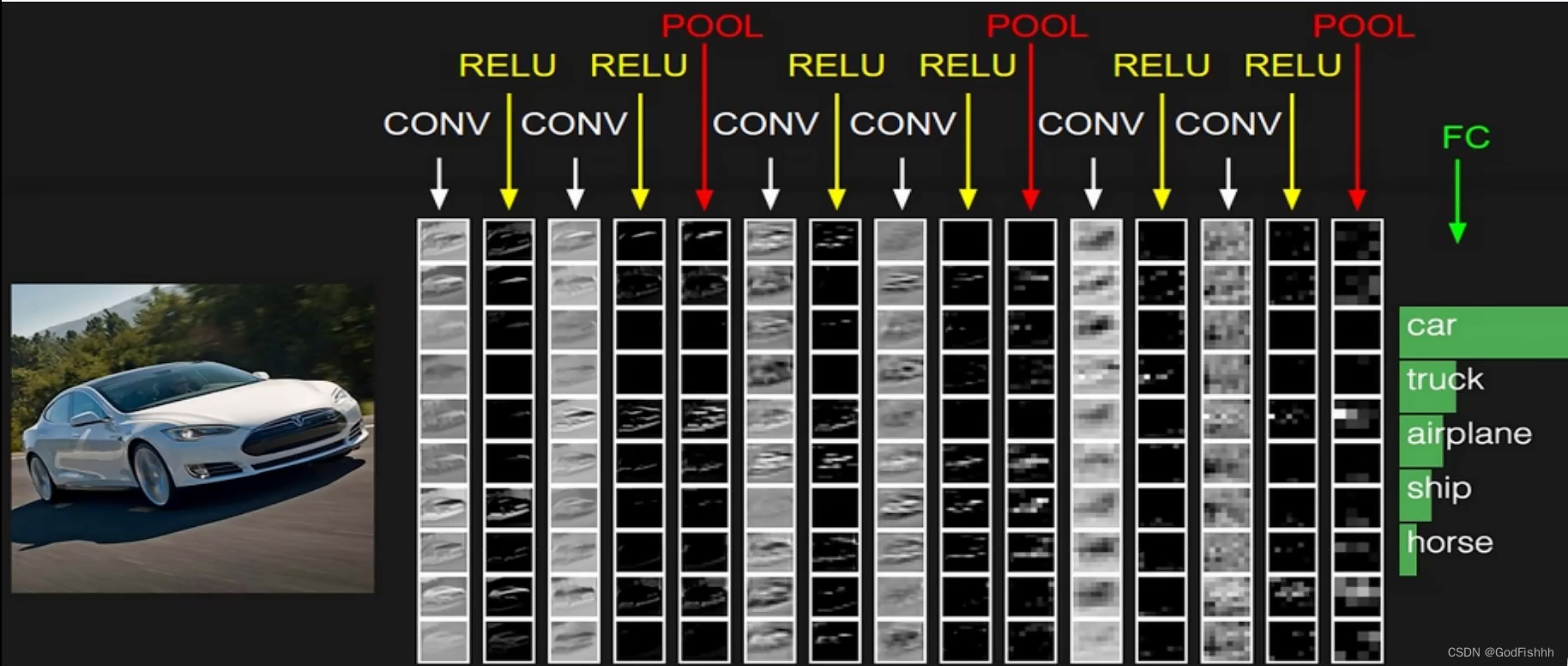
1.经过每个卷积层计算后都需要进行一次非线性变换（CONV → RELU)。

2.执行了几次卷积过程后，得到较大的特征图，再进行池化POOLING压缩。

3.最后一层通过全连接层（Fully Connected Layer）将特征值转换为对应类别的概率值。

eg.卷积最后得到一个32x32x10的三维特征图，而全连接层不是三维的，所以要将三维特征图拉长成一个[1,10240]的向量，全连接向量为[10240,5]，两者向量相乘得到最后的分类结果。

4.层数一般就是指具有权重/参数的层数总和，即卷积层+全连接层，上图中的卷积神经网络中有6（卷积层) + 1（全连接层）=7 层。

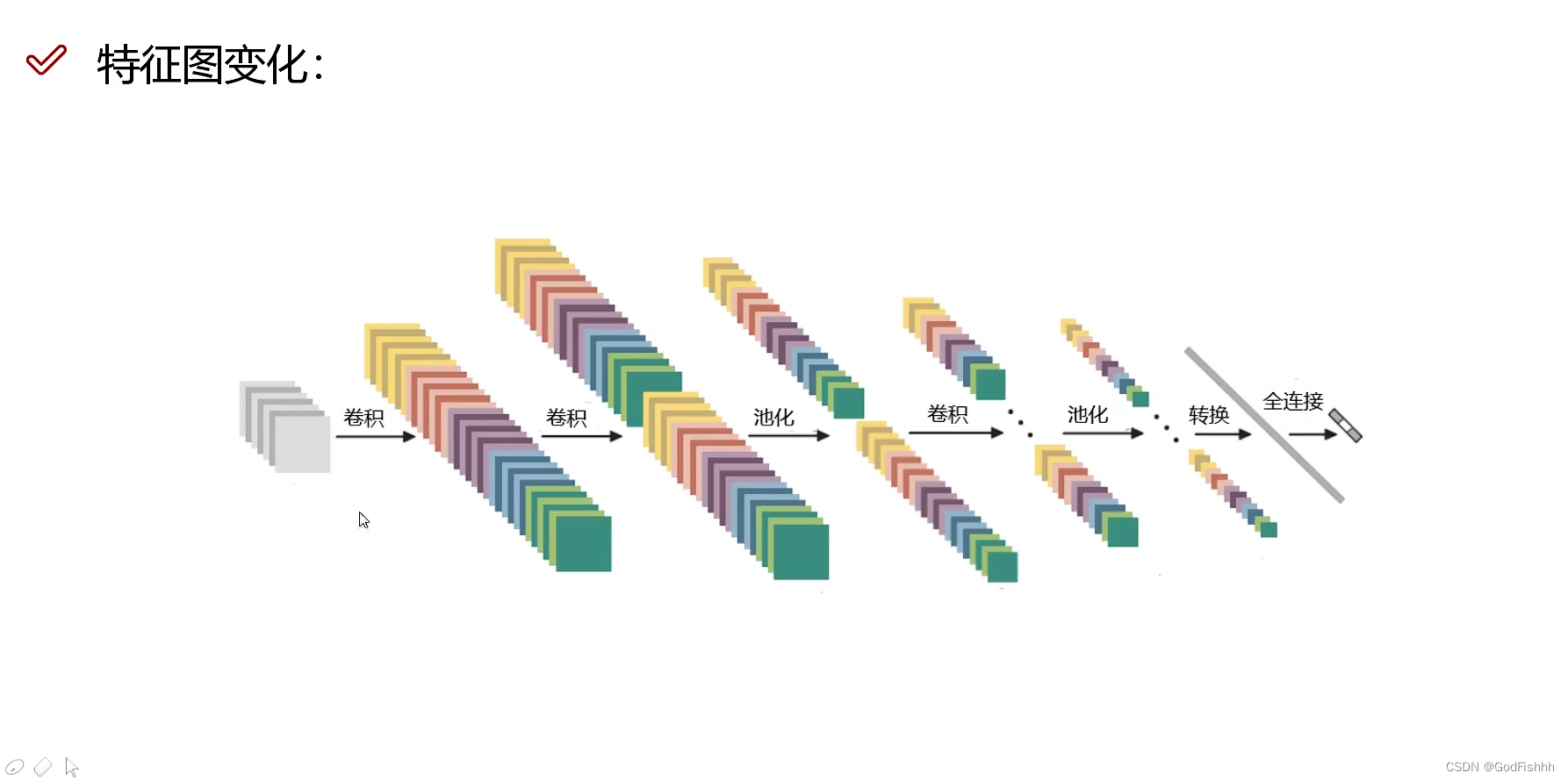
 六.感受野

感受野（Receptive Field）的定义：卷积神经网络每一层输出的特征图（feature map）上的像素点映射回输入图像上的区域大小

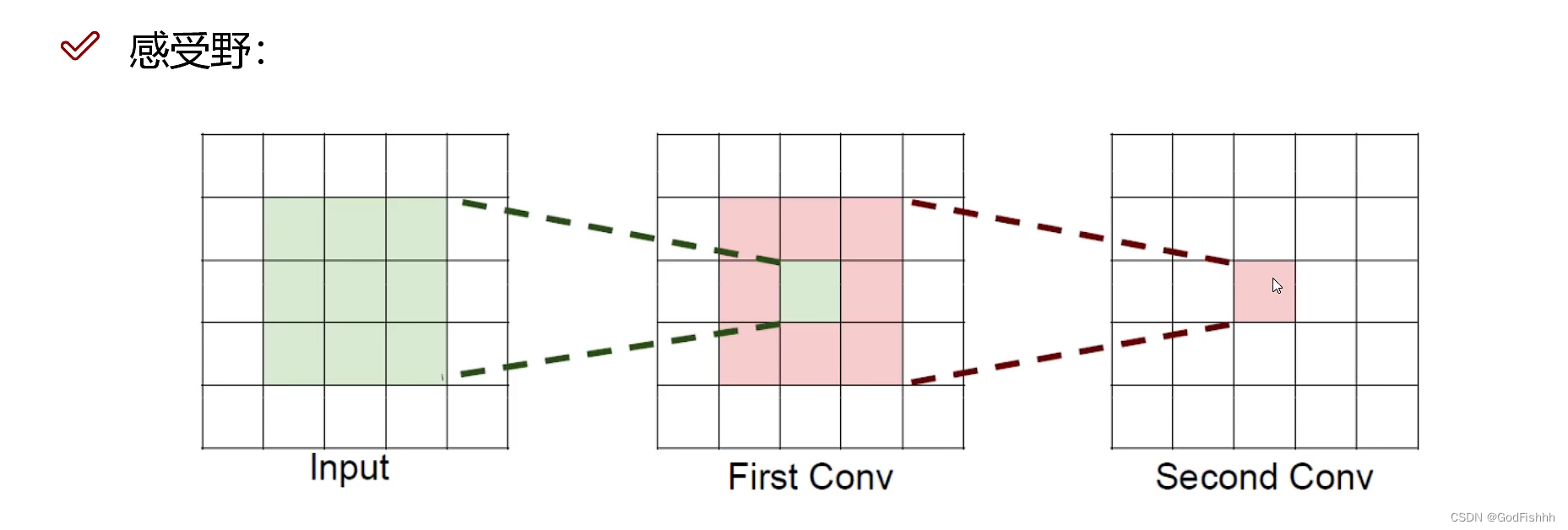
如上图所示，第二次卷积得到的1x1的图像的感受野为5x5：Second Conv对应的First Conv的部分为3x3，First Conv对应Input的部分为5x5，所以Second Conv得到的图像的感受野为5x5。

感受野的计算：

由卷积计算公式反推出感受野计算公式：

N=(W-F+2P)/S+1 → W+2P=(N-1)*S+F（从下往上逐层递推）

其中N为输出特征图的长/宽，W为输入的长/宽，F表示本层卷积核的长/宽，P表示边界填充，S为滑动窗口步长。

eg.Second Conv → First Conv：(W+2P)1 = (1-1) * 0 + 3 = 3 ，所以感受野为3x3，First Conv → Input ：(W+2P)2 = （3-1）*1 + 3 = 5，所以最终的感受野为5x5。

1.感受野大小的计算是从最后一层feature map开始，从下往上逐层递推进行计算，即先计算最深层在前一层上的感受野，然后以此类推逐层传递到第一层。

2.感受野大小的计算不考虑padding的大小。

3.最后一层的特征图感受野的大小等于其卷积核的大小。(最后一层特征图的大小为1x1)

4.第i层特征图的感受野大小和第i层的卷积核大小和步长有关系，同时也与第（i+1）层特征图的感受野大小有关。

感受野的作用：

1.堆叠小的卷积核所需要的参数更少一些。

eg.假设输入大小均为h*w*c,并且都使用c个卷积核（得到c个特征图）

一个7*7卷积核所需参数：C x (7x7xC) = 49C^2 -- 一次卷积

三个3*3卷积核所需参数：3 x C x (3x3xC) = 27C^2 -- 三次卷积

2.卷积过程越多，特征提取的也更加细致，过程中使用的非线性变换也更多。(每次卷积后需要使用激活函数进行一次非线性变换）