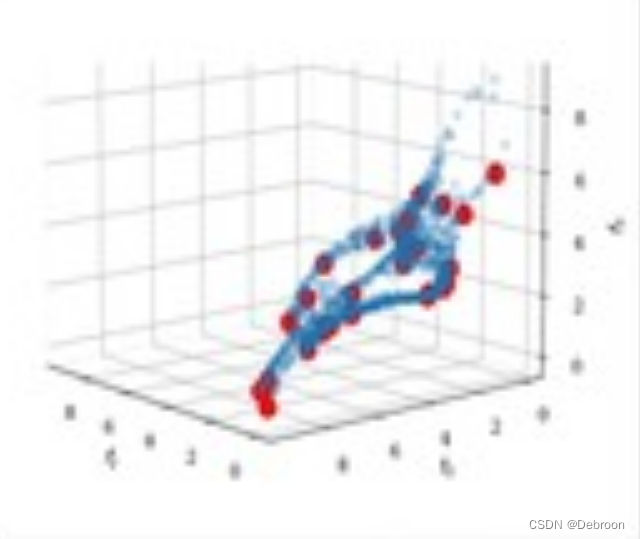
构建函数又名构造函数，是欧系数学的重要解题方法。构建函数最成功的范例是“1/n＞ln(1+1/n)”，它来自欧拉，其手段极其卑劣下作！随心所欲、目空一切是欧拉的习惯

欧拉证明1/n＞ln(1+1/n)的操作有两步：①先构建函数“ln(1+x)”，显见x＞ln(1+x)成立；②设“x=1/n”，由第一步易得1/n＞ln(1+1/n)成立。——如果我生在18世纪，我一定会指着欧拉的鼻子破口大骂：你这不叫解题！你这是在恬不知耻地耍流氓！

不了解欧拉的人，不知道欧拉做学问潦草如儿戏；了解了欧拉，就能发现潦草作弊是他的风格，在证明1/n＞ln(1+1/n)问题上，他的方法就是放肆地作弊：为了实现Σ1/n＞lnn目标，欧拉需要1/n＞ln(1+1/n)；为了获得1/n＞ln(1+1/n)，就构造一个函数“ln(1+x)”、并令x＞ln(1+x)，尔后再设x=1/n，于是就得到了1/n＞ln(1+1/n)。这就好比我不是大学生，假设我家里是一所大学，于是我就是大学生。不经历上流社会生活，你根本臆想不到上层人的龌龊，见识了欧拉的造假操作，方知这个“神中之神”有多么得猥琐！

自欺欺人尺是欧拉惯用的工具

 有以下几点可以看出“1/n＞ln(1+1/n)”的造假是故意欺诈：第一，ln(1+x)毫无意义，因为ln(1+x)就是lnx；构建ln(1+x)的唯一目的是扯出ln(1+1/n)，那为何不直接构建ln(1+1/n)？因为ln(1+1/n)涉及到小数，小数之下“1/n＞ln(1+1/n)”一眼就有违和感、糊弄不了观众；那么构建ln(1+x)能避开小数吗？显然不可能，x取集范围是“＞0”，用构建ln(1+x)、以避开小数的用心乃痴心妄想！第二，本命题x、n为同一个定义或数集，设x=1/n就是设x=1/x，这在任意层面都绝对不允许；就数学规则而言，对x成立、对1/x必然不成立(别拿x=1说事儿)；第三，y=x的函数图像，从0→1与从1→n是截然相反的两种趋势，1→n无限趋近x轴、0→1无限趋近y轴，换言之：ln(1+x)的取集必须界定x≥1、0＜x＜1，否则构建ln(1+x)可以，想“易得x＞ln(1+x)”没门！

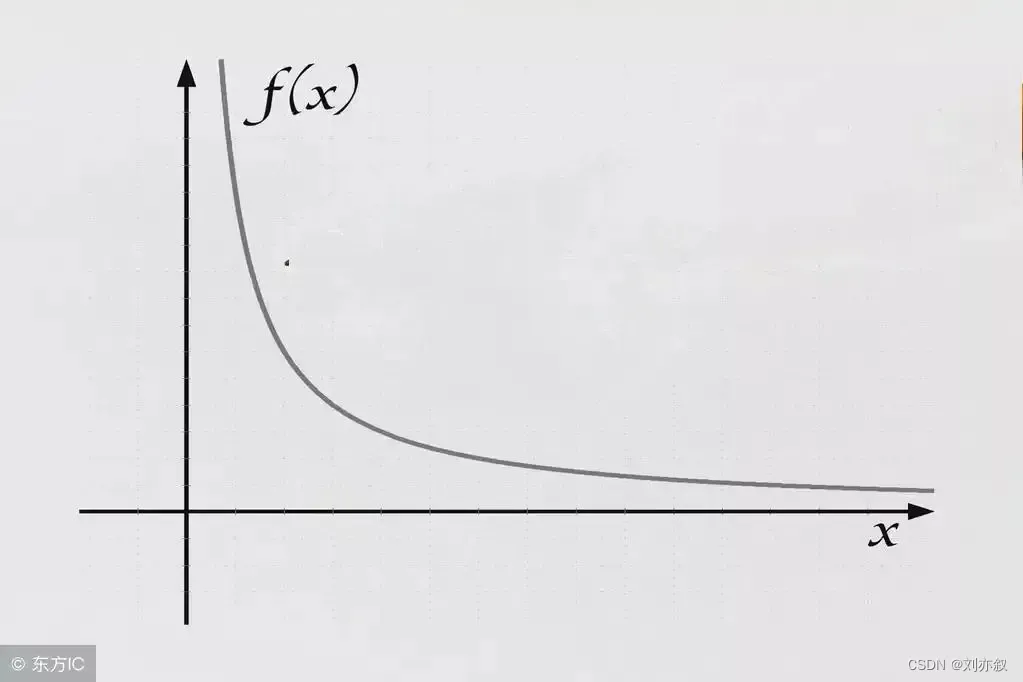x＜1与x＞1是反函数，不能混为一谈

 x＞ln(1+x)成立只能限于x≥1，1/n＞ln(1+1/n)并不一定成立。欧拉构建函数“ln(1+x)”的表演用自我愚弄已不能概括本质，它就是彻头彻尾的造假！

x与ln(1+x)、1/n与ln(1+1/n)趋势相反

 “1/n＞ln(1+1/n)”涉嫌故意造假，证据①.1/n→0、ln(1+1/n)→常数，0＞常数反常识反数理；证据②.运用硬算累加法，每一个e^6.93级或者10³级，ln(1+1/n)较1/n多增值0.0223…，ln(1+n)将在n=e^60或者10^26时上穿Σ1/n；证据③.利用算式求和法，ln(1+1/n)的基础数值每翻1倍，积分值恒提升1倍，而对应的1/n基础值每翻1倍，和值分别提升0.8333…、0.7595…、0.7253…、……，显然彼此不是对等趋势，1/n下穿ln(1+1/n)是必然的。

铁证如山，欧拉用构建函数猫腻搞出来的“1/n＞ln(1+1/n)”实锤为学术欺诈！