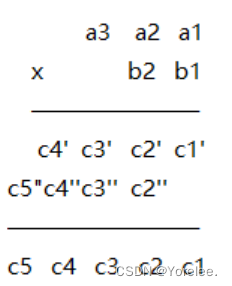代码的第一遍真的很重要,在第一次打的时候尽量把问题思考全面,不要漏打少打,尽量不要留bug给之后de。
一、基础方面
一、处理输出的结束问题
scanf和cin默认都不会读取空格
①scanf():如果从文件中读取数据,当scanf()返回值是EOF时,则读取结束。
while(scanf("%d",&num)!=EOF) {}②cin>>:cin是有返回值的,若是从文件中读取数据,到达文件末尾就读取结束了,读取到文件尾部,cin返回值是false。
while(cin>>num) {}
二、读取带空格的字符串
①scanf:使用[],[]内是匹配的字符,^表示求反集。
char s[100]; scanf("%[^\n]",s);可以读取[^\n]表示所有字符里面去掉换行符
②cin:使用string类中的getline()函数
string s; getline(cin,s);③gets()或getchar()
三、超大数据类型
__int128:16个字节、占用128bit的整数存储类型。由于是二进制,范围就是 -2^127~2^127-1,如果使用了
unsigned __int128,则范围变成 0 ~ 2^128-1,即约十进制39位数。在不超过该数据范围时,可以用它来替代高精度计算。它只能使用+、-、*、/四则运算,不能使用cin、cout等,要输入这样的数据则必须先输入为字符串,然转换成数据。
四、string
string s;
s.size()是一个无符号整型,如果在进行减法时,比如s.size()-t,t>s.size(),则会溢出,得不到需要的负数。
二、算法方面
一、高精度
long long只能表示大约19位十进制数,如果位数高于19位,那么普通的整型已经不够存储了,我们需要使用高精度存储和计算来解决这样的问题。
高精度算法本质上是用字符串模拟数字进行计算,再利用类似于数学里的竖式的形式,一位一位进行相关计算 .
C++ 算法 高精度(较详细.)_c++高精度-CSDN博客
高精度算法
在进行高精度计算时,除了除法之后,其余的+、-、*都需要对数字进行逆序存储,因为两个数的位数可能是不一样的,这导致在计算的时候下标会不一样,逆序存储就可以解决这样的问题,也可以解决进位问题。
①加法:
加法存在进位,我们将进位存储在x中,对于位数更小的数,补充0,这样这种算法可以直接进行计算,用0加就行了!
int x=0; int a[100]={}; int b[100]={}; int c[101]={}; 逆序存储a和b while(c_len<=a_len||c_len<=b_len){ c[c_len]=a[c_len]+b[c_len]; x=c[c_len]/10; c[c_len]%=10; c_len++; } if(x) c[c_len]=x; else c_len--; //至此0~c_len就是 逆序的结果
对于不明长度时的加法:用while去遍历到临界条件是最好的方式(包括其他问题),然后再判断是谁的临界,然后再进行一次操作即可。ps:while循环一定要记得++i,--i的操作!
vector<int> cur; vector<int> now; //cur和now已经逆序存放,目的将cur+now结果存入cur中 int x=0; int i=0; while(i<cur.size()&&i<now.size()){ cur[i]=cur[i]+now[i]+x; x=cur[i]/10; cur[i]=cur[i]%10; ++i; } //cur小的时候 if(i==cur.size()){ for(;i<now.size();++i){ int temp=now[i]+x; cur.push_back(temp%10); x=temp/10; } } if(x) cur.push_back(x);②减法:
减法存在借位问题,同样逆序存储,借位直接加在本位上,即使借位让高位变成-1也没关系,因为它还会继续借位变成9,当然我们需要判断大小,被减数当最大的,然后添负号即可。
int a[100]={}; int b[100]={}; int c[100]={}; 逆序存储a和b if(a<b){//伪代码 flag=true; swap(a,b); } while(c_len<=a_len||c_len<=b_len){ if(a[c_len]<b[c_len]{ a[c_len]+=10; a[c_len+1]--; } c[c_len]=a[c_len]-b[c_len]; c_len++; } while(c[c_len]==0&&c_len>0) --c_len;//前面的0是无效的,如果结果是0需要保存 if(flag) 添加负号③乘法:
乘法和加法一样有进位,乘法可以理解为,多次进行被乘数乘以一位乘数,然后把多次结果相加得到最终结果。
int a[100]={}; int b[100]={}; int c[200]={}; 逆序存储a和b for(int i=0;i<a_len;++i){//让a当做乘数,一位一位乘 int x=0; //每次乘都有一个进位 for(int j=0;j<b_len;++j){ c[i+j]+=x+a[i]*b[j];//c[k]表示结果中逆序第k+1位的数字,需要累加起来 x=c[i+j]/10; c[i+j]%=10; } c[i+b_len]+=x;//最后的进位,当时进位可以是0,少个判断直接相加。 } c_len=a_len+b_len-1;//最大位数-1 但是不一定 while(c[c_len]==0&&c_len>0) --c_len; //至此0~c_len为所求结果④除法:
(1)高精度除以低精度
高精度除以低精度,低精度的数可以直接存储在一个整型中,从高精度最高位开始除,除不够上商上0(对于前导0最后直接忽略即可),除得够就上商上1~9,余数在下一次除时乘以10加上下一位,继续除。
int a[200]={}; int b; int c[100]={}; 正序存储a,确保b不为0 int x=0; for(int i=0;i<a_len;++i){ c[i]=(x+a[i])/b; x=(x+a[i])%b; x*=10; } int j=0; while(c[j]==0&&j<a_len-1) ++j; //至此j~a_len-1为所求结果(2)高精度除以高精度
高精度除法,在做除法的时候只能用高精度减法模拟,可以减多少次就上商为几,余下来的就是余数。我们可以善用vector比较大小的特性,比较大小的时候必须是长度相等的时候才有意义。
#include<bits/stdc++.h> using namespace std; vector<int> a; vector<int> b; int divide(vector<int> & res,vector<int> & b){//保证够减,高精度减 模拟 一次除法 int num=0; vector<int> x=b; reverse(x.begin(),x.end()); while(res.size()>b.size()||(res.size()==b.size()&&res>=b)){ reverse(res.begin(),res.end()); vector<int> c; ++num; for(int i=0;i<res.size();++i){ if(res[i]<x[i]){ res[i]+=10; res[i+1]--; } c.push_back(res[i]-x[i]); } while(c.size()>0&&c[c.size()-1]==0) c.pop_back();//为0的余数不要了,原因是我们的res会继续为后面的除法做贡献,前导0对后续除法来说无意义,甚至影响判断~ res=c; reverse(res.begin(),res.end()); } return num; } int main(void){ /*--------------初始化-----------------*///确保初始化没有前导0。 string s; cin>>s; for(int i=0;i<s.size();++i) a.push_back(s[i]-'0'); cin>>s; for(int i=0;i<s.size();++i) b.push_back(s[i]-'0'); /*--------------除法-----------------*/ vector<int> res;//余数 vector<int> q;//商 for(int i=0;i<a.size();++i){ res.push_back(a[i]); if(res.size()<b.size()){//位数不够 q.push_back(0); }else{ if(res.size()==b.size()&&res<b){//位数刚好够,但是没它大 q.push_back(0); }else{ q.push_back(divide(res,b));//返回商,并且引用式参数,余数res会自动更改。 } } } printf("结果的余数是:"); if(res.size()){ for(int i=0;i<res.size();++i) cout<<res[i]; cout<<endl; }else{ cout<<0<<endl; } int j=0; while(j<q.size()-1&&q[j]==0) ++j; printf("结果的商是:"); for(;j<q.size();++j) cout<<q[j]; return 0; }
二、M进制转N进制
一、十进制转N进制基本思路
我们看十进制X转N进制,十进制在转成N进制的时候,我们可以这样考虑:
rn rn-1 rn-2 rn-3 ······· r4 r3 r2 r1 r0 <rn是结果最高位,r0是最低位>
①当前X%N,就是N进制的最低位r0,因为除了最低位的其他位对应的十进制权值都是最低位的N倍。
②然后我们让X=X/N,我们可以发现此时的十进制X转换成N进制的结果一定是:
rn rn-1 rn-2 rn-3 ······· r4 r3 r2 r1<rn是结果最高位,r1是最低位>
③循环①②步,直到X=0,去掉最高位0即可以得到答案。
二、M进制转N进制
M进制的X转N进制,可以这样考虑,对于一个M进制数:
an an-1 an-2 an-3 ······· a4 a3 a2 a1 a0 <an是最高位,a0是最低位>
其十进制值X1可以写为:
int x1=0; for(int i=n;i>=0;--i){ x1*=M; x1+=ai; }在往后遍历的过程中an的权值会不断乘以M倍,直到最后就变成了M^n。
我们再来看为其除以N:
an*M^(n)+an-1*M^(n-1)+an-2*M^(n-2)+····+a3*M^3 +a2 *M^2+a1*M+a0
——————————————————————————————————
N
我们注意到ai<M,则有an*M^(n)会包含十进制中的最高位,我们同样从高位除起,
①an/N=qn········rn [an*M^(n)=qn*N*M^(n)+rn*M^(n)]
可以知道qn*M^(n)也必然包含商中十进制的最高位,同时由于an<M,则qn必然<M。
rn留给后一位
②(rn*M+an-1)/N=qn-1····rn-1 [(rn*M+an-1)*M^(n-1)=qn-1*N*M^(n-1)+rn-1*M^(n-1)]
假设rn=M-1<N(拉到最大),则(M-1)*M+an-1=qn-1*N+rn-1,设qn-1=M(超过M的最小值),则(M-1)*M+an-1=M*N+rn-1,则an-1=(N-M+1)*M+rn-1,由于N+1>M,则N-M+1>0,整数下N-M+1>=1,则an-1>=M矛盾,所以qn-1=M不成立,换而言之qn-1<M。
rn-1留给后一位。
以此类推:
最终我们的值实际上是:
an*M^(n)+an-1*M^(n-1)+an-2*M^(n-2)+····+a3*M^3 +a2 *M^2+a1*M+a0
=(qn*M^(n)+qn-1*M^(n-1)+qn-2*M^(n-2)+····+q3*M^3 +q2 *M^2+q1*M+q0)*N+r0
由以上可知qn qn-1 ···q0 仍然是一个M进制的数。
在转换时,用上述等式来看,an除以N上商上qn,余数*M进入下一位
#include<bits/stdc++.h> using namespace std; int M,N; int main(void){ string s; cin>>M>>N; cin>>s; vector<int> nums; string res; //---------------------初始化---------------------------- for(int i=0;i<s.size();++i){ if(s[i]>='A') nums.push_back(s[i]-'A'+10); else nums.push_back(s[i]-'0'); } //--------------M进制转N进制:高精度除法------------------- while(nums.size()){ int x=0; for(int i=0;i<nums.size();++i){ nums[i]+=x*M; x=nums[i]%N; nums[i]/=N; } if(x<=9) res.push_back(x+'0'); else res.push_back(x-10+'a'); while(nums.size()&&nums[0]==0) nums.erase(nums.begin()); } if(res.back()=='0') res.pop_back(); //---------------------输出结果------------------------- for(int i=res.size()-1;i>=0;--i) cout<<res[i]; return 0; }
三、BUG方面
一、变量初始化
我们这里将的变量初始化,并不是指初始化变量让其不会表示一个内存中的随意数。我们指的是在一个每次循环的操作都意义一样时,有的变量需要每一次循环都初始化一次,如果不进行初始化,上一次循环的结果会影响下一次循环。
比如:在进行十进制转二进制高精度转换时,flag用来表判断数位中的1是借位,还是原来的1,对于每一次循环,target都是一个新的数,这个时候flag都需要重新赋值为false。一个常见的错误是把flag在定义时赋值为false,在循环开头没管了,之后debug也很难发现这一条问题。如果对这种赋值有警觉性,或者脑袋清醒,就不会犯这样的错误!
当时实际做题时,使用高精度除以低精度算法即可。
二、while循环条件变量
while(i>0&&q[i]==0) {q.pop_back();--i;}你忘了--i,你可以尝试养成一个习惯,当写这样的while语句时,先把++i,--i给写上,不然最后可能写完一长串内容,不再看一次循环就已经忘了还有++i这个东西。