文章目录
- 1.x 的平方根
- 2.第一个错误的版本
- 3.有效的完全平方数
- 4.猜数字大小
- 5.排列硬币
- 6. 寻找比目标字母大的最小字母
- 7. 二分查找
- 8.检查整数以及其两倍数是否存在
- 9. 两个数组间的距离值
- 10.特殊的数组的特征值
- 11.找出数组排序后的目标下标
- 12.和有限的最长子序列
- 13.正整数和负数的最大计数
- 14.最小公共值
- 15.统计和小于目标的下标对数目
- 16.LCP.早餐组合
- 16.LCP.采购方案
- 17.LCR.两数之和 || - 输入有序数组
- 18. LCR 搜索插入位置
- 19.LCR 山脉素组的峰顶索引
- 19.寻找旋转排序数组中的最小值
- 20.LCR.统计目标成绩出现的次数
- 21.LCR.点名
- 22.LCR.查找总价格为目标值的两个商品
- 23.魔术索引
本篇是二分枚举,其中所有题都可以用线性枚举做出来,还有的双指针也可以。
建议先线性枚举做一遍,然后知道求什么后,再去想着二分去求。
本篇的解法中只有二分枚举,没有线性枚举。
1.x 的平方根

- 不适用库函数哈。
- 我使用二分法,举两个例子,8和9。
- 使left 和 right 分别等于 1 和 x。
- 然后取其中间值mid,
- 如果mid*mid > x,right = mid;
- 如果mid*mid < x, left = mid;
- mid*mid = x ,return mid;
- 还有一种情况就是如果left + 1 == right 也就是说 left 和mid相邻的时候,直接返回left就好了
int mySqrt(int x)
{
long long left = 1,right = x,mid;
while(left + 1 != right)
{
mid = (left + right) / 2;
if(mid * mid > x)
{
right = mid;
}
else if(mid * mid < x)
{
left = mid;
}
else
{
return mid;
}
}
return left;
}
2.第一个错误的版本

- 首先得知道这个isBadVersion函数使质量合格返回false,不合格返回true。
- 然后对其进行二分查找就好了
int firstBadVersion(int n)
{
int left = 1, right = n;
while(left < right)
{
//防止溢出
int mid = left + (right - left) / 2;
if(isBadVersion(mid))
{
//不合格 [left,mid]
right = mid;
}
else
{
//[mid+1,right]
left = mid + 1;
}
}
return left;
}
3.有效的完全平方数

- 上面第一题ok了,下面这道题也就ok了
bool isPerfectSquare(int num)
{
long long left = 1,right = num;
while(left + 1 != right)
{
long long mid = (left + right) / 2;
if(mid * mid > num)
{
right = mid;
}
else if (mid * mid < num)
{
left = mid;
}
else
{
return true;
}
}
return false;
}
4.猜数字大小

- 嗯。。。。。。
int guessNumber(int n)
{
int left = 1,right = n;
while(left != right)
{
int mid = left + (right - left) / 2;
int flag = guess(mid);
if( flag == -1)
{
//比mid小
right = mid - 1;
}
else if(flag == 1)
{
//比mid大
left = mid + 1;
}
else
{
return mid;
}
}
return left;
}
5.排列硬币

- 在两个数中间去二分的查找一个合适的mid,找到mid后
- 求出mid所对应的等差数列和,(mid * (mid + 1))/ 2;
- 如果和 小于 硬币,就证明下一行可能继续放,所以left = mid
- 如果和 大于 硬币,就证明当前这一行,肯定使不行了,所以使right = mid
- 如果等于的话,返回mid就好了
- 最后就使介于两个数中间,left + 1 == right.
- 返回那个小的即可
int arrangeCoins(int n)
{
long long left = 1,right = n;
while(left + 1 != right)
{
long long mid = left + (right - left) / 2;
long long sum = (mid*(mid+1)) / 2; //等差数列
if(sum > n)
{
//放的多了
right = mid;
}
else if (sum < n)
{
left = mid;
}
else
{
return mid;
}
}
return left;
}
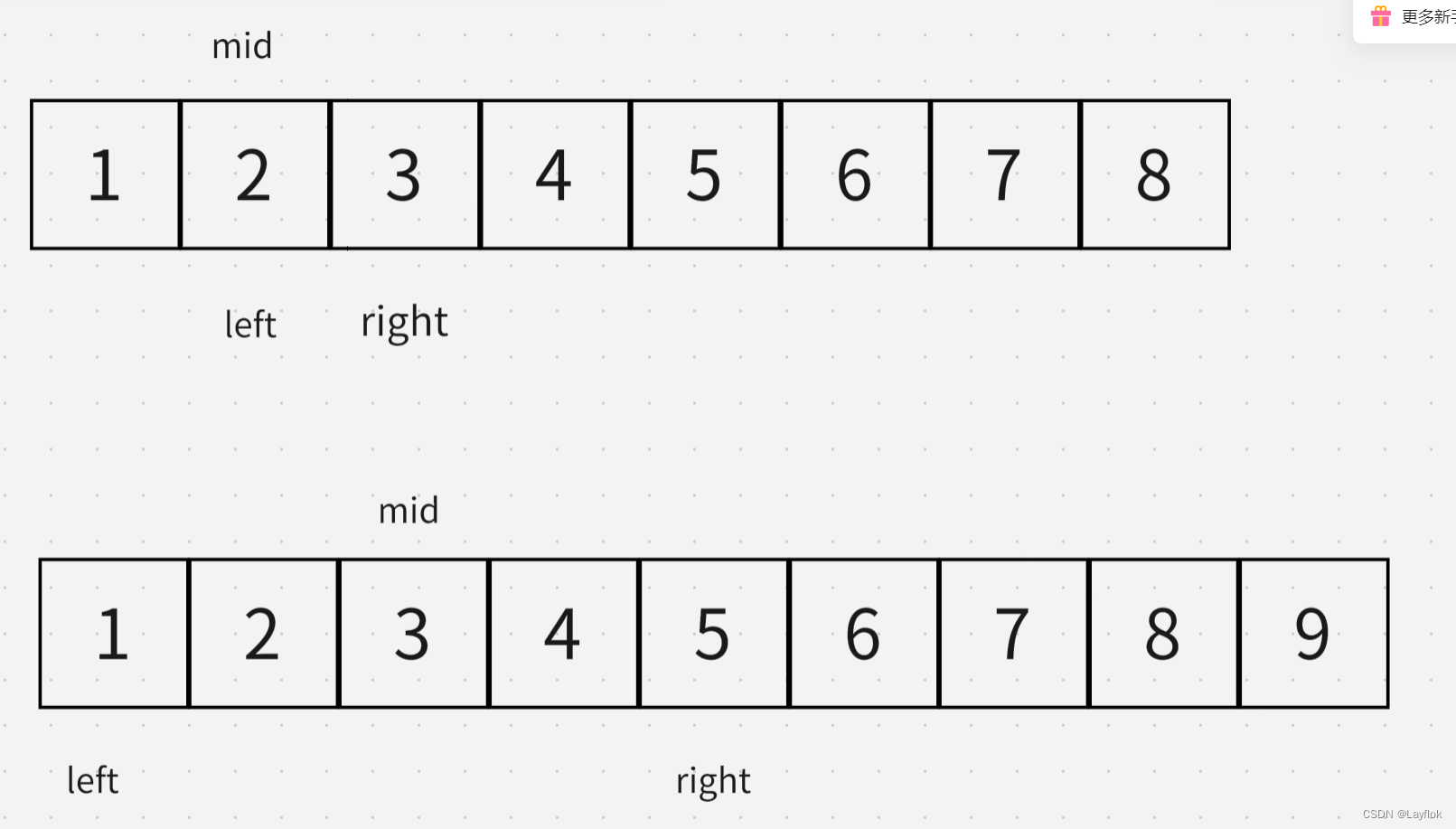
6. 寻找比目标字母大的最小字母

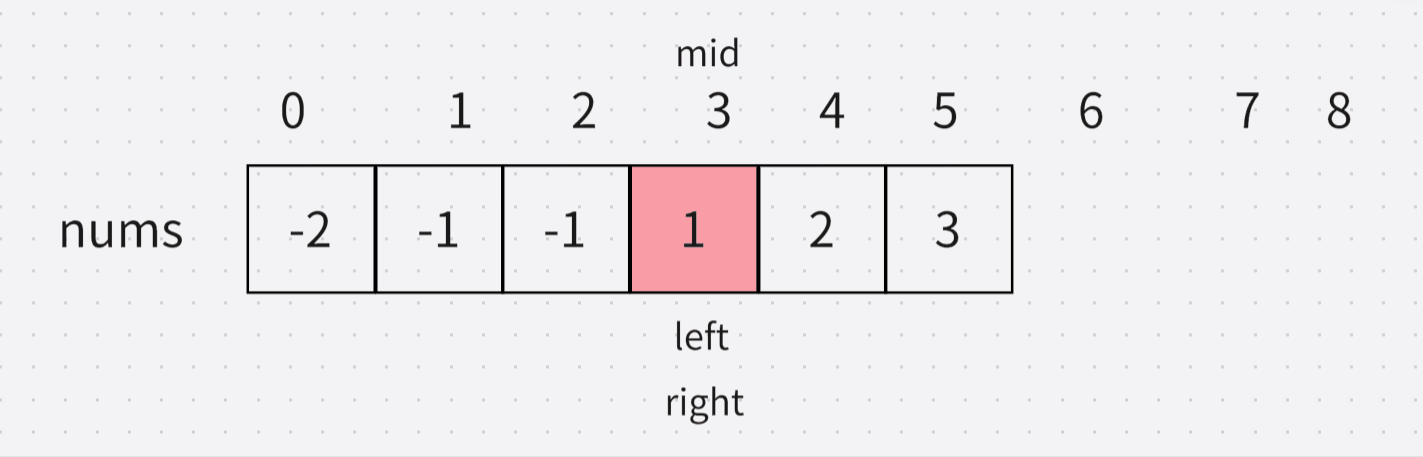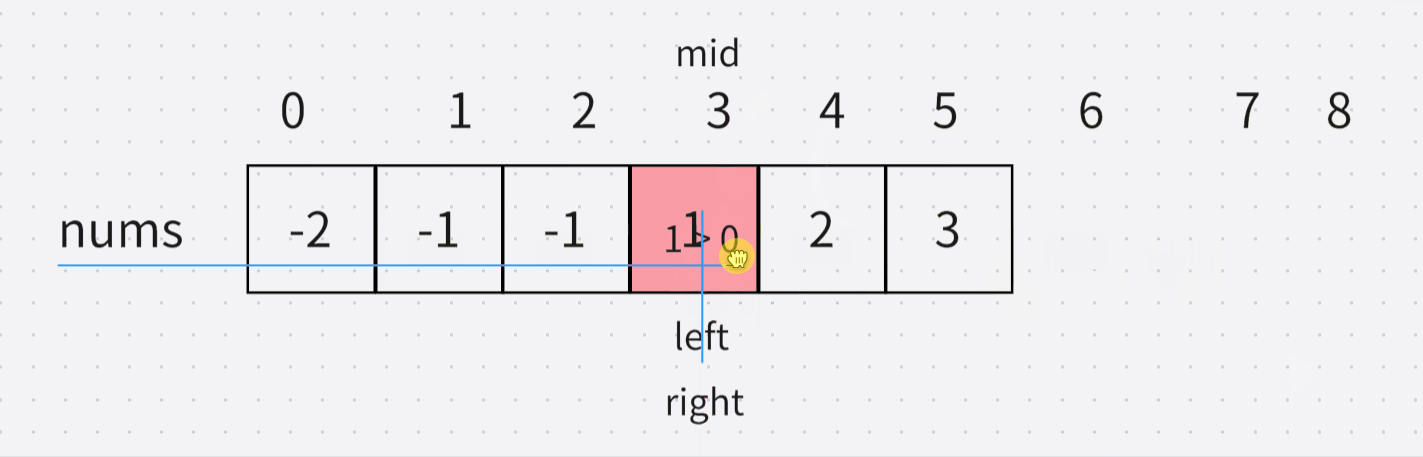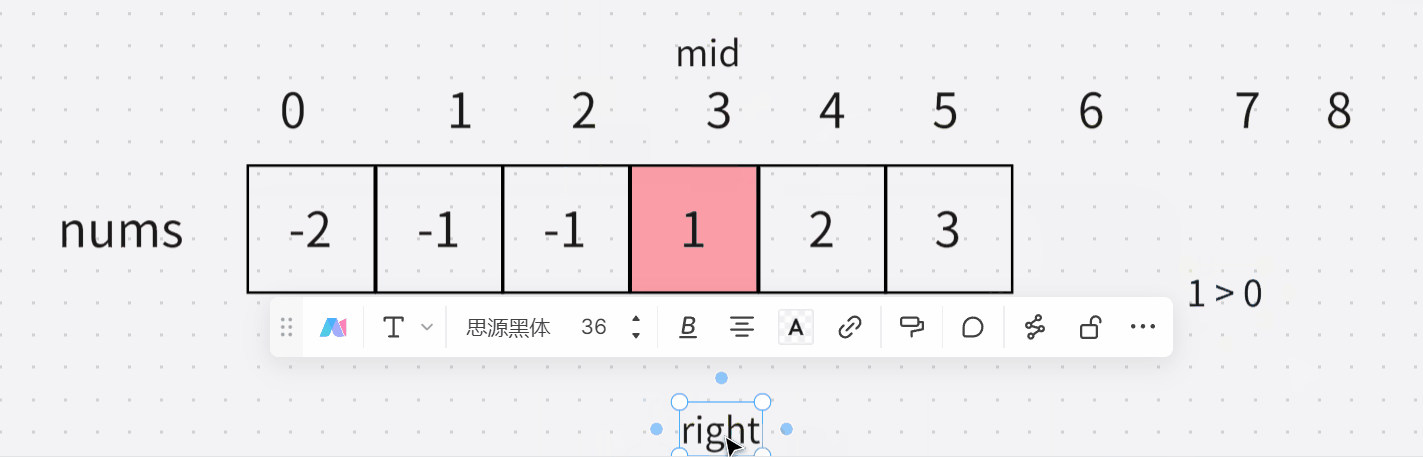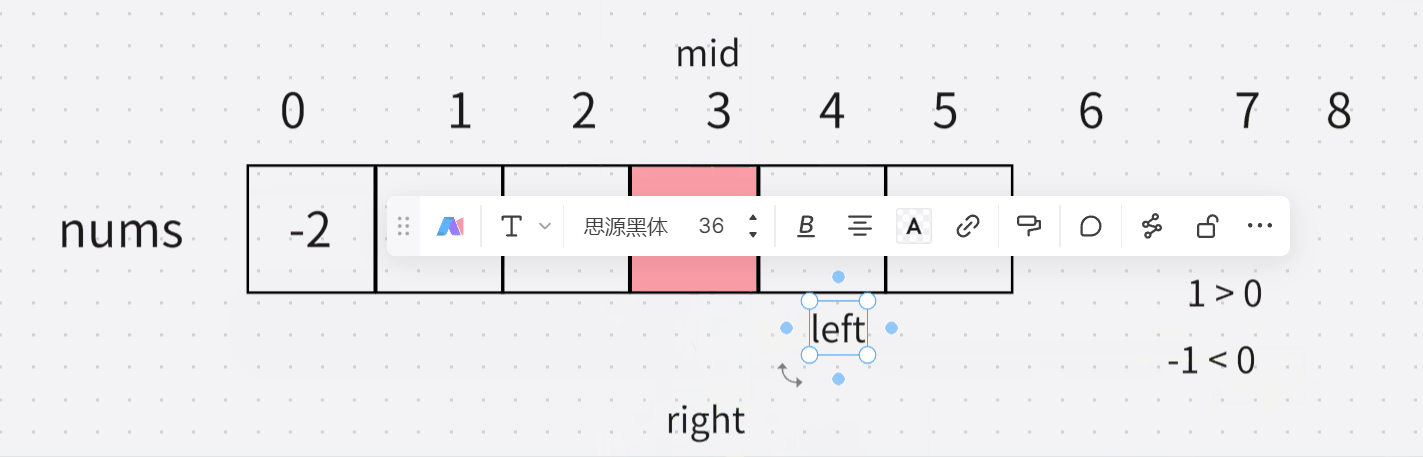
- 这个字符数组是一个升序的数组,如果target 大于等于 最后一个,就说明里面肯定没有比target更大的了,返回数组第一个即可
- 如果mid 大于 target 那么肯定使 right 变小
- 如果mid 小于 target 那么肯定使 left 变大
- 当他俩错过时候,返回left所在的位置即可
结合下面两张图可以理解


char nextGreatestLetter(char* letters, int lettersSize, char target)
{
if(target >= letters[lettersSize-1])
{
return letters[0];
}
int left = 0, right = lettersSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(letters[mid] > target)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return letters[left];
}
7. 二分查找

- 嗯。。。经典,其实应该放在第一道题去刷的。绝对得是二分查找
int search(int* nums, int numsSize, int target)
{
int left = 0,right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] < target)
{
left = mid + 1;
}
else if (nums[mid] > target)
{
right = mid - 1;
}
else
{
return mid;
}
}
return -1;
}
8.检查整数以及其两倍数是否存在

- 暴力,和哈希,也能做出来。
- 这里就先用二分吧
- 首先将数组进行排序,然后往前遍历,要注意,如果当前数的二倍是负数,需要往前找。
代码逻辑:
bool checkIfExist(int* arr, int arrSize)
{
//升序排序
qsort(arr,arrSize,sizeof(arr[0]),cmp_int);
int i;
for (i = 0; i < arrSize - 1; i++)
{
int target = arr[i] * 2;
//printf("%d target = %d\n",arr[i],target);
if( target >= 0 && BinSearch(arr + i + 1,arrSize - i - 1,target))
{
//正数往后找
return true;
}
else if(BinSearch(arr,i,target))
{
//负数往前找
return true;
}
}
return false;
}
函数:
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
bool BinSearch(int* nums,int numsSize,int target)
{
int left = 0,right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else if(nums[mid] < target)
{
left = mid + 1;
}
else
{
return true;
}
}
return false;
}
9. 两个数组间的距离值

- 这道题,暴力枚举会更简单,更直接的想到,我第一遍就是暴力过的
- 这里写一下二分的方法吧
- 首先二分的前提下一定是得有序的。
- 所以,先给arr2进行排序。
- 然后去arr2里面去找那个离arr1[i]中距离最近的那个数。
- 如果离arr1[i]最近的数与arr1[i]的差距都 > d
- 那样不就证明其余的都满足了吗?
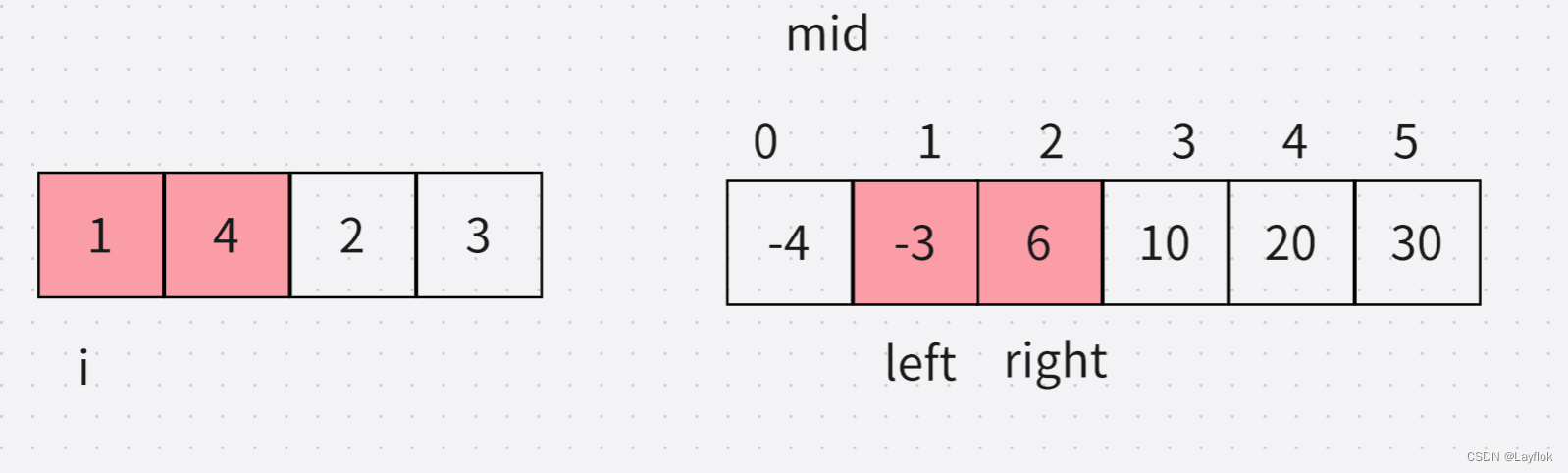
但是出现了一个问题,就是我二分的时候,确定不了那个数,我只能确定两个,然后再单独判断哪一个更近,就比如下图中,不管查找1 和 4,都会再 -3 和 6 的时候停下来。
但是和1相邻的是-3 和 4 相邻的则是 6。
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
int BinSearch(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize -1;
int leftgarp = 0,rightgarp = 0;
while(left + 1 != right && numsSize != 1)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid;
}
else if(nums[mid] < target)
{
left = mid;
}
else
{
return nums[mid];
}
}
leftgarp = abs(nums[left] - target);
rightgarp = abs(nums[right] - target);
return leftgarp < rightgarp ? nums[left] : nums[right];
}
int findTheDistanceValue(int* arr1, int arr1Size, int* arr2, int arr2Size, int d)
{
int i,j,ans = 0;
qsort(arr2,arr2Size,sizeof(int),cmp_int);
for (i = 0; i < arr1Size; i++)
{
//找出距离arr1[i]最近的那个数
int near = BinSearch(arr2,arr2Size,arr1[i]);
if(abs(arr1[i] - near) > d)
{
ans++;
}
}
return ans;
}
10.特殊的数组的特征值

- 暴力肯定也是行得通的,暴力的目的,就是在nums中找出大于等于 x 的元素个数.
int specialArray(int* nums, int numsSize)
{
int i,j;
for (i = 0; i <= numsSize; i++)
{
int count = 0; //记录有多少数据个大于i
for (j = 0; j < numsSize; j++)
{
if(nums[j] >= i)
{
count++;
}
}
if(count == i)
{
return i;
}
}
return -1;
}
上面的代码中是用线性枚举的方式去找,而当然也可以用二分枚举的方式去找。
int specialArray(int* nums, int numsSize)
{
int i,j;
qsort(nums,numsSize,sizeof(int),cmp_int);
for (i = 0; i <= numsSize; i++)
{
int count = BinSearch (nums,numsSize,i); //记录有多少数据个大于i
if(count == i)
{
return i;
}
}
return -1;
}
代码逻辑是一样的,主要还得是看看这个二分到底是如何实现的,就是普通二分法还不行,因为它里面会有重复的元素。下面这张图中,不可以直接返回nums - mid。因为左边还有一个6会被忽视掉,所以在代码中得变一变条件
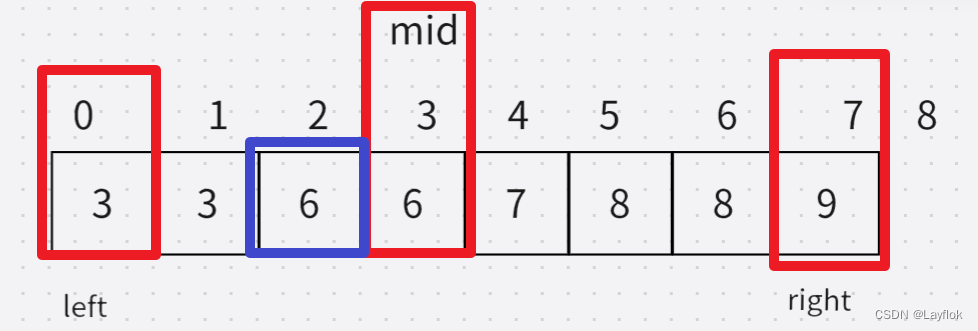
- 但凡用到二分法,数组一定得是有序的,同样的计算出mid
- nums[mid] >= right, right = mid
- nums[mid] < right, left = mid + 1;
- 当left 等于right 时候,还得去判断一下 当前的这个数,是否大于等于所给的target,
- 如果大于返回numSize - left(right)
- 如果小于的话,肯定返回0.
//找出里面有多少个 >= target 的元素个数
int BinSearch(int* nums,int numsSize,int target)
{
int left = 0, right = numsSize - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] >= target)
{
right = mid;
}
else if(nums[mid] < target)
{
left = mid + 1;
}
}
return nums[left] >= target ? numsSize - left : 0;
}
11.找出数组排序后的目标下标

- 首先将数组进行排序,然后对其进行二分。
- 找到所对应的target后,对其左边右边进行遍历,如果发现有重复的,将其也记录下来
- 最后再给ans数组进行排序就好了
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
int* targetIndices(int* nums, int numsSize, int target, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * numsSize);
int size = 0,i;
qsort(nums,numsSize,sizeof(int),cmp_int);
int left = 0, right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else if(nums[mid] < target)
{
left = mid + 1;
}
else
{
int l = mid - 1,r = mid + 1;
//当前的
ans[size++] = mid;
//左边
while(l >= 0 && nums[l] == target)
{
ans[size++] = l--;
}
//右边
while(r < numsSize && nums[r] == target)
{
ans[size++] = r++;
}
break;
}
}
qsort(ans,size,sizeof(int),cmp_int);
*returnSize = size;
return ans;
}
12.和有限的最长子序列

- queries(查询)就是去nums当中,找出 子序列 和 小于等于 queries[i]的长度。
- 题目中最后一句话的意思就是说,只要是数组内的数据就行,所以我们可以先将数组排序。
- 然后利用排好序的数组计算出每个所对应的前缀和

- 有了前缀和的数组,就可以去二分查找所对应的 queries[i]。
- 有下面两种情况
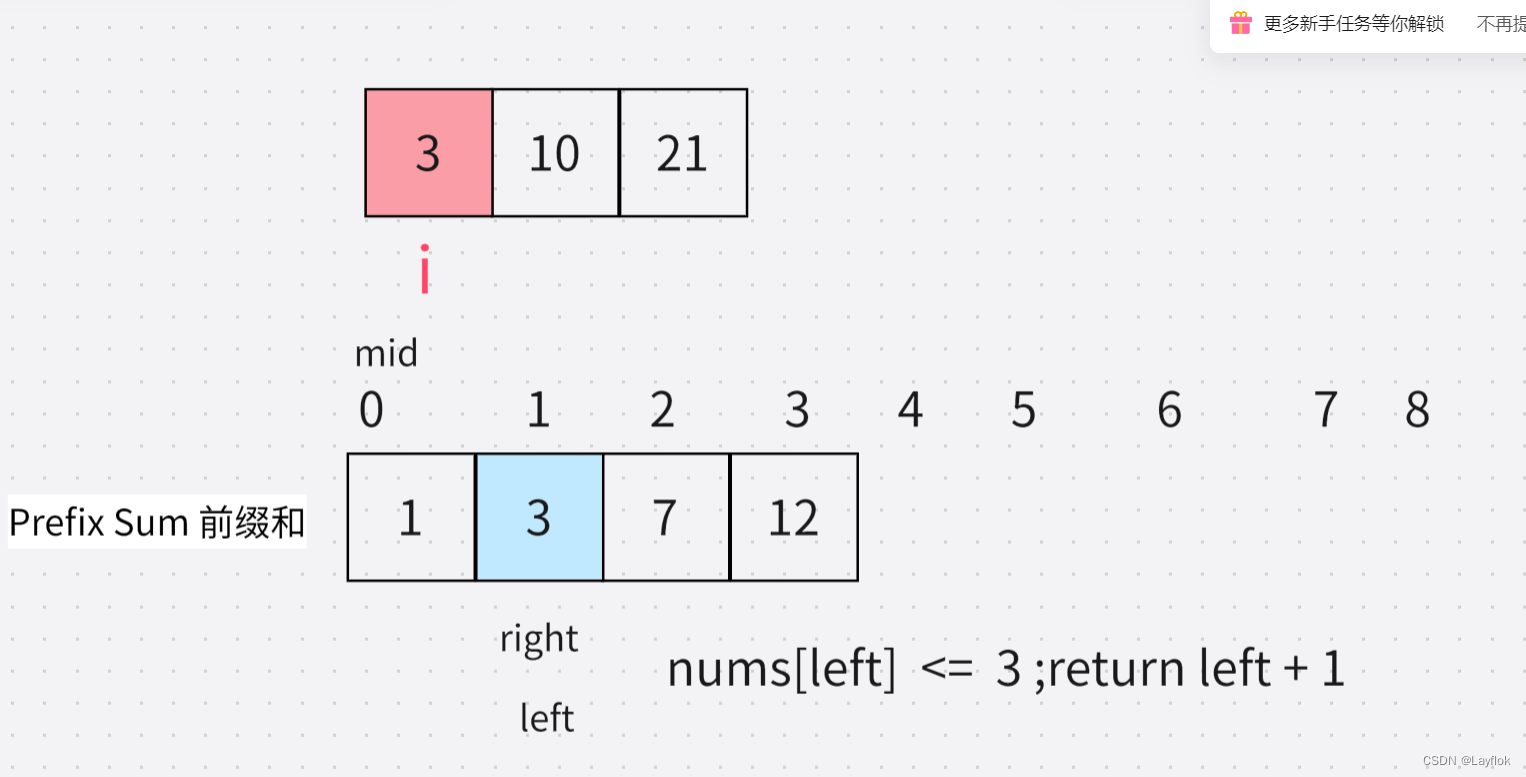
这种情况下,题目中要求 <= 所以当前的也能取上,而left是下标,所以得 + 1
而下面这种,12 大于10 就意味着,肯定不能取到12,所以返回前面的三个即可
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
int BinarySearch(int* nums, int numsSize,int target)
{
int left = 0,right = numsSize - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] < target)
{
left = mid + 1;
}
else
{
right = mid;
}
}
return nums[left] > target ? left : left + 1;
}
int* answerQueries(int* nums, int numsSize, int* queries, int queriesSize, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * queriesSize);
int size = 0,i,j;
//排序
qsort(nums,numsSize,sizeof(int),cmp_int);
//前缀和数组
int* prefixsum = (int*)malloc(sizeof(int) * numsSize);
int sum = 0;
for (i = 0; i < numsSize; i++)
{
sum += nums[i];
prefixsum[i] = sum;
}
//找每一个对应的长度
for (i = 0; i < queriesSize; i++)
{
ans[size++] = BinarySearch(prefixsum,numsSize,queries[i]);
}
*returnSize = size;
return ans;
}
13.正整数和负数的最大计数

- 这道题,和上面11题一样,我这道题是如果找到0的话,就分开两头去找最近的一个不是0的数。
要注意的是,下面的代码逻辑,不管如何,
都是right 代表最后一个负数出现位置,
left 代表一个正数出现的位置
看下图,不管是 1 或者 -1 都是不会改变上面的逻辑的
int maximumCount(int* nums, int numsSize)
{
int pos = 0, neg = 0;
int left = 0, right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > 0)
{
right = mid - 1;
}
else if (nums[mid] < 0)
{
left = mid + 1;
}
else
{
// 发现是0,分开去找,
right = mid - 1;
left = mid + 1;
//左边
while(right >= 0 && nums[right] == 0)
{
right--;
}
//右边
while(left < numsSize && nums[left] == 0)
{
left++;
}
break;
}
}
pos = numsSize - left;
neg = right + 1;
return pos > neg ? pos : neg;
}
14.最小公共值

- 这道题,感觉双指针更快一点。
- 下面是二分的解法:
- 把nums1想象成一个target数组,去nums2中去找是否有nums[1]中的值即可
int BinarySearch(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else if(nums[mid] < target)
{
left = mid + 1;
}
else
{
return true;
}
}
return false;
}
int getCommon(int* nums1, int nums1Size, int* nums2, int nums2Size)
{
int i;
for (i = 0; i < nums1Size; i++)
{
if(BinarySearch(nums2,nums2Size,nums1[i]))
{
return nums1[i];
}
}
return -1;
}
15.统计和小于目标的下标对数目

- 下面是暴力的做法:记住下面的nums[i] + nums[j] < target。后面会用到
int countPairs(int* nums, int numsSize, int target)
{
int i,j,count = 0;
for (i = 0; i < numsSize; i++)
{
for (j = i + 1; j < numsSize; j++)
{
if(nums[i] + nums[j] < target)
{
count++;
}
}
}
return count;
}
由题可知,我们只需要扎找到两个不同的下标 i 和 j 就好了。但是不能重复,比如说下图中

这个是题目中示例一排序后的数组,就是 nums[0] + nums[1] < 2. 但是不能nums[1] + nums[0] < 2.
这个就叫重复,也可以像题目中那样说 i < j,所以排序不会影响最后的结果。
而不重复的就是,你在传数组的时候,不用将自身传过来,从下一个的位置开始传
上面的暴力中会发现,我们呢是需要找 j,但是这个是线性枚举的找j方式,我们只需要换成二分枚举即可。
看下面的推到公式,简单的不等式对吧。 所以不等式右边的,就是在二分中与mid进行比较的值
- 有了上面的两个思想,二分就简单了,不可重复与mid与谁作比较.
- 下面是代码。
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
int BinartSearch(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] < target)
{
left = mid + 1;
}
else
{
right = mid;
}
}
return nums[left] < target ? left + 1 : left;
}
int countPairs(int* nums, int numsSize, int target)
{
int i,j,count = 0;
qsort(nums,numsSize,sizeof(int),cmp_int);
for (i = 0; i < numsSize - 1; i++)
{
count += BinartSearch(nums + i + 1,numsSize - i - 1,target - nums[i]);
}
return count;
}
16.LCP.早餐组合

- 和上题一样,这个上题更简单,因为有两个数组,不用那么麻烦的考虑,在一个数组里传来传去。
- 你饮料不可以超过 x - staple[i]。
int cmp_int(const void* x,const void* y)
{
return *(int*)x - *(int*)y;
}
long long BinarySearch(int* nums, int numsSize, int target)
{
long long left = 0, right = numsSize - 1;
while(left < right)
{
long long mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return nums[left] <= target ? left + 1 : left;
}
int breakfastNumber(int* staple, int stapleSize, int* drinks, int drinksSize, int x)
{
int i,j;
long long count = 0;
qsort(drinks,drinksSize,sizeof(int),cmp_int);
for (i = 0; i < stapleSize; i++)
{
count += BinarySearch(drinks,drinksSize,x - staple[i]);
}
return (int)(count % 1000000007);
}
// mid <= x - staple[i]
16.LCP.采购方案

- 这道题和上一题是类似的。
int cmp_int(const void* x, const void* y)
{
return *(int*)x - *(int*)y;
}
long long BinarySearch(int* nums, int numsSize, int target)
{
long long left = 0, right = numsSize - 1;
while(left < right)
{
long long mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return nums[left] <= target ? left + 1 : left;
}
int purchasePlans(int* nums, int numsSize, int target)
{
int i;
qsort(nums,numsSize,sizeof(int),cmp_int);
long long count = 0;
for (i = 0; i < numsSize - 1; i++)
{
if(nums[i] > target)
{
break;
}
count += BinarySearch(nums + i + 1, numsSize - i - 1,target - nums[i]);
}
return (int)(count % 1000000007);
}
17.LCR.两数之和 || - 输入有序数组

- 二分时候需要找的target 是 target - numbers[i]。
- 还有要注意的是从i+1 的位置开始找,i以前数肯定都不行,也不允许自己加自己
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int BinarySearch(int* nums,int left, int right, int target)
{
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid -1;
}
else if (nums[mid] < target)
{
left = mid + 1;
}
else
{
return mid;
}
}
return -1;
}
int* twoSum(int* numbers, int numbersSize, int target, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * 2);
int i;
for (i = 0; i < numbersSize; i++)
{
int index = BinarySearch(numbers,i + 1,numbersSize - 1,target - numbers[i]);
if(index != -1)
{
ans[0] = i;
ans[1] = index;
}
}
*returnSize = 2;
return ans;
}
这道题其实用双指针的效果也很好。
/**
* Note: The returned array must be malloced, assume caller calls free().
*/
int* twoSum(int* numbers, int numbersSize, int target, int* returnSize)
{
int left = 0, right = numbersSize - 1;
int* ans = (int*)malloc(sizeof(int) * 2);
*returnSize = 2;
while(left < right)
{
int sum = numbers[left] + numbers[right];
if(sum > target)
{
right--;
}
else if(sum < target)
{
left++;
}
else
{
ans[0] = left;
ans[1] = right;
break;
}
}
return ans;
}
18. LCR 搜索插入位置

- ok啦。
int searchInsert(int* nums, int numsSize, int target)
{
int left = 0, right = numsSize - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] < target)
{
left = mid + 1;
}
else
{
right = mid;
}
}
return nums[left] < target ? left + 1 : left;
}
19.LCR 山脉素组的峰顶索引

- 如果发现nums[mid] > nums[mid + 1]。它可能是峰顶,因为并没有与它的前一个去教,无法判断
-
- 所以此时使 right = mid - 1

- 所以此时使 right = mid - 1
- 如果nums[mid] < nums[mid + 1],它不可能是峰顶,
- 使left = mid +1;
int peakIndexInMountainArray(int* arr, int arrSize)
{
int left = 0, right = arrSize - 2,ans = 0;
while(left <= right)
{
int mid = (left + right) / 2;
if(arr[mid] > arr[mid + 1])
{
//记录当前的这个峰值
ans = mid;
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return ans;
}
19.寻找旋转排序数组中的最小值
- 额。。听我说,我在这里套娃呢,先使打开普通,又是打开困难,最后打开中等。
- 只看简单题,没理解其中的意思,简单题目中描述,并没有说数组使有序旋转过的,我还以为,原来使有序的现在变成了无序。想了半天,硬使没想通,为啥这个无序的能用二分?
- 这三道题的测试用例,也使有不同的。
- 举两个例子吧。
这种情况是我们可以直接发现,直接想到的。
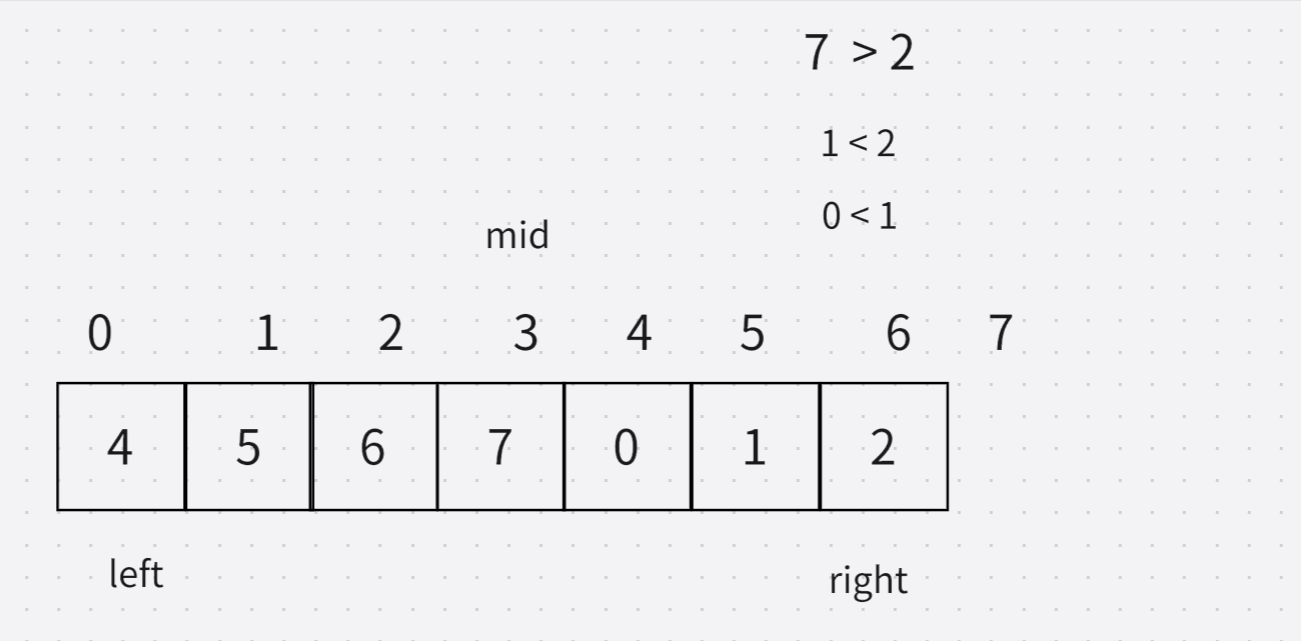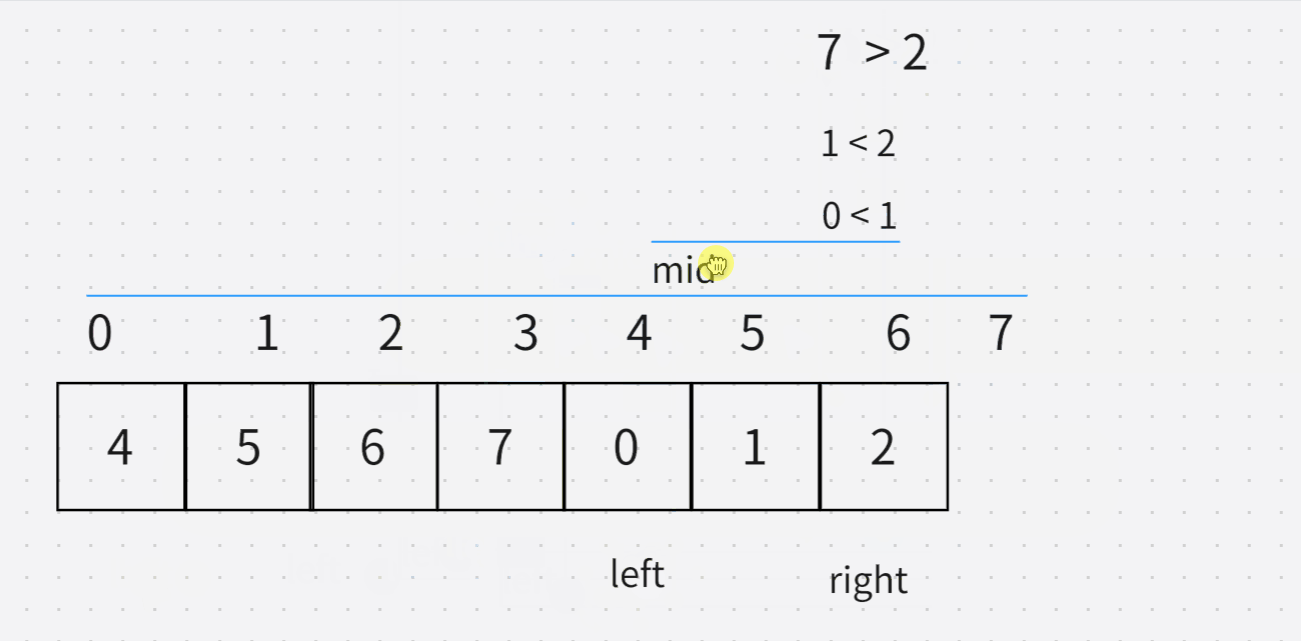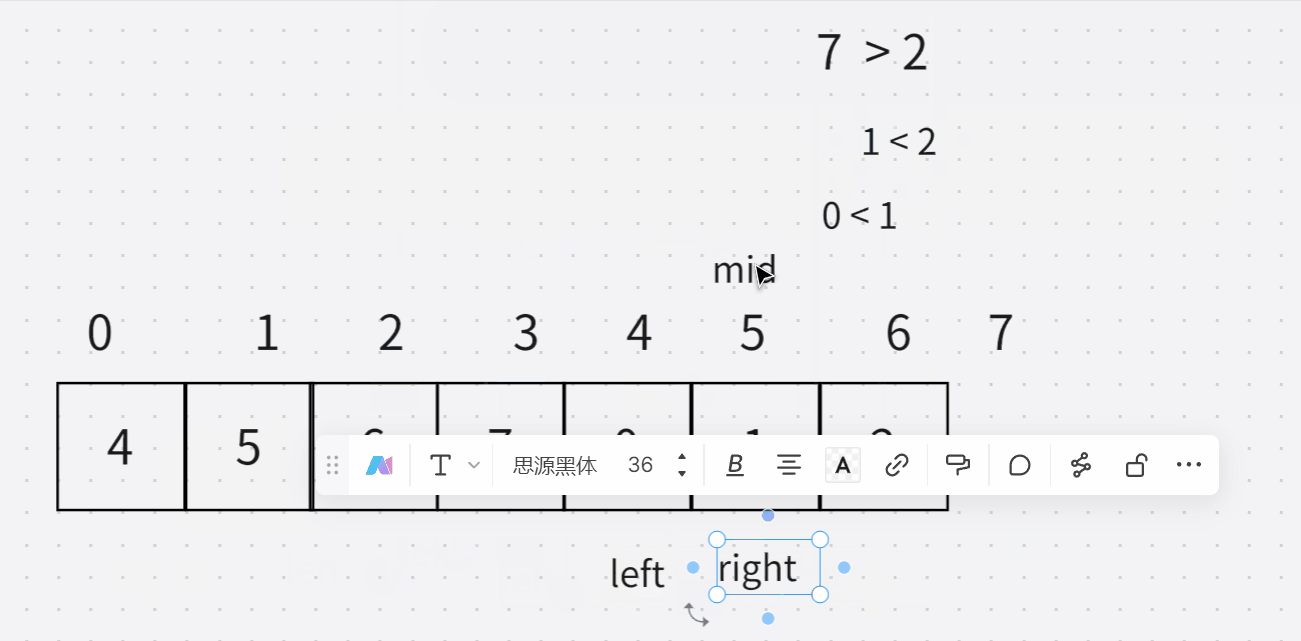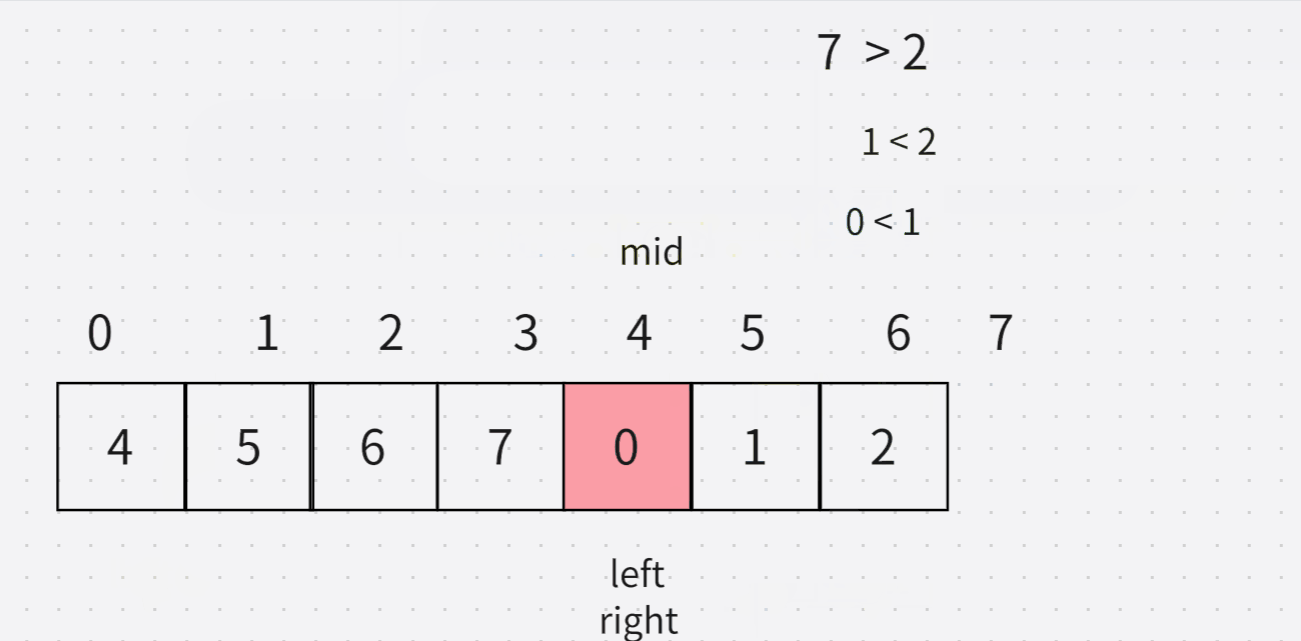
下面这主要是知道,为什么相同的时候,得right–。
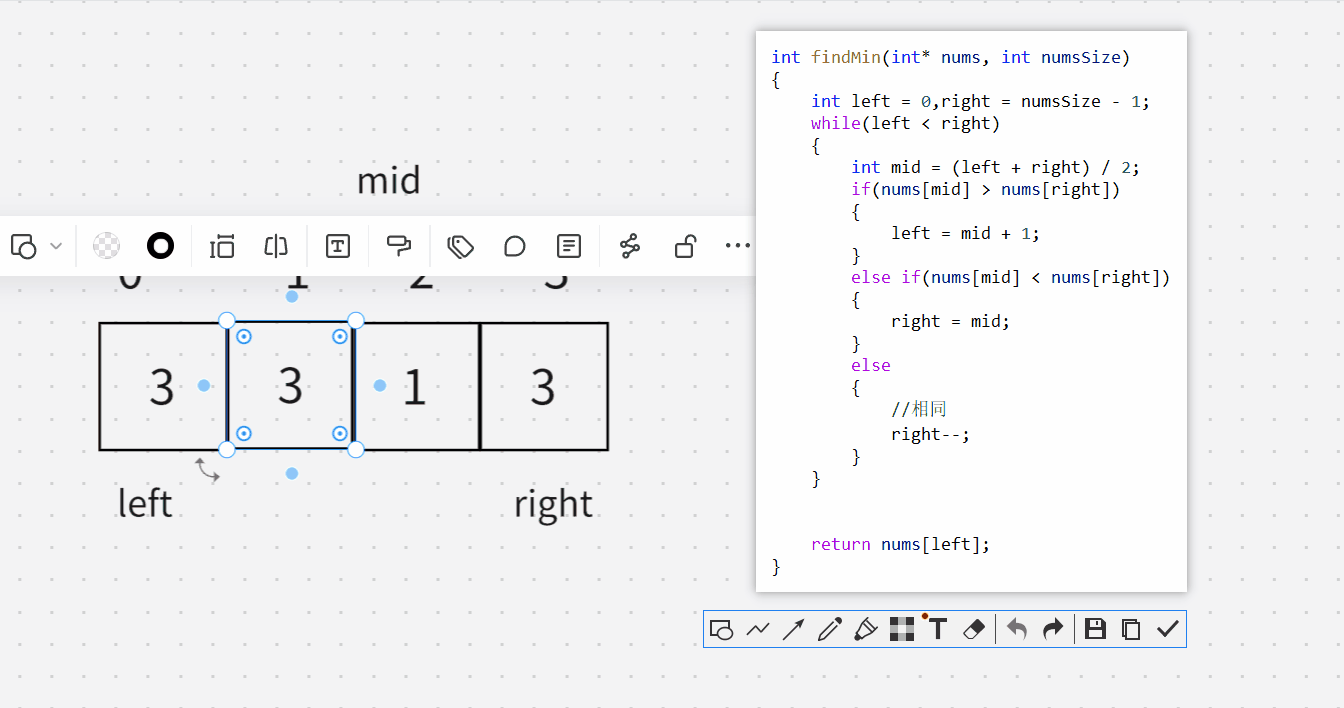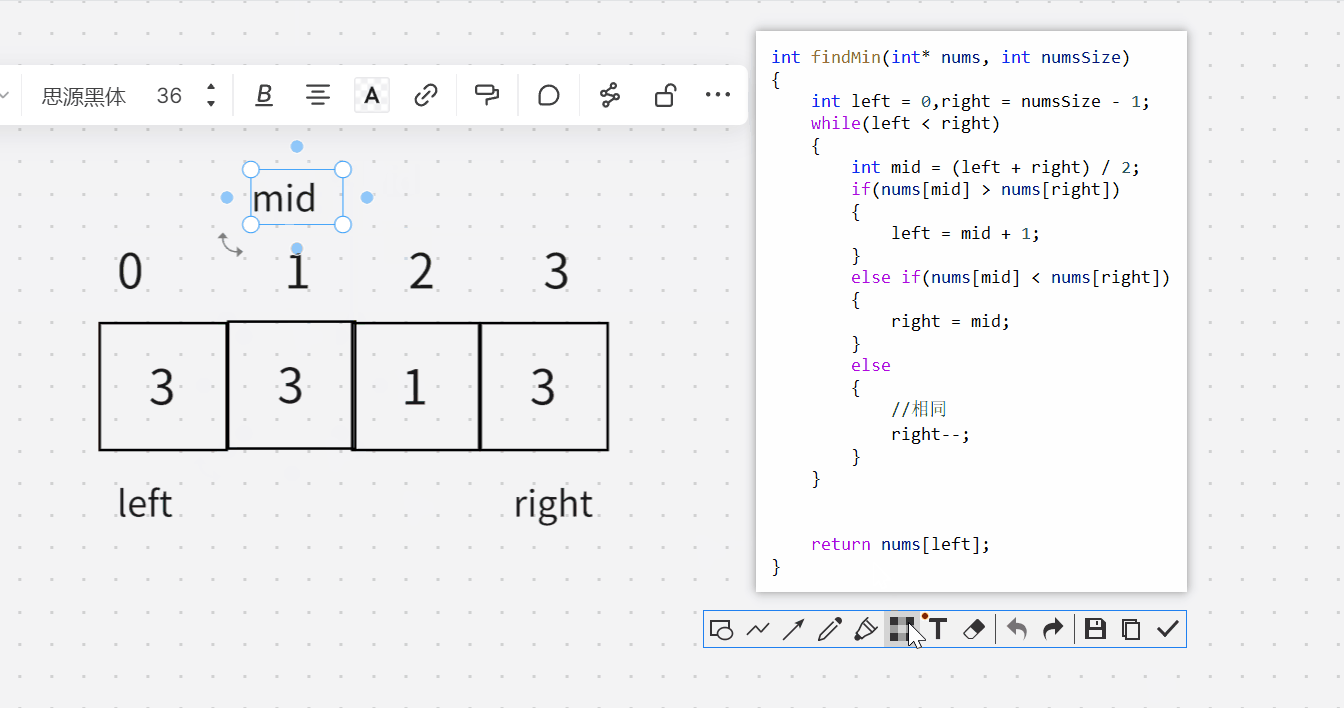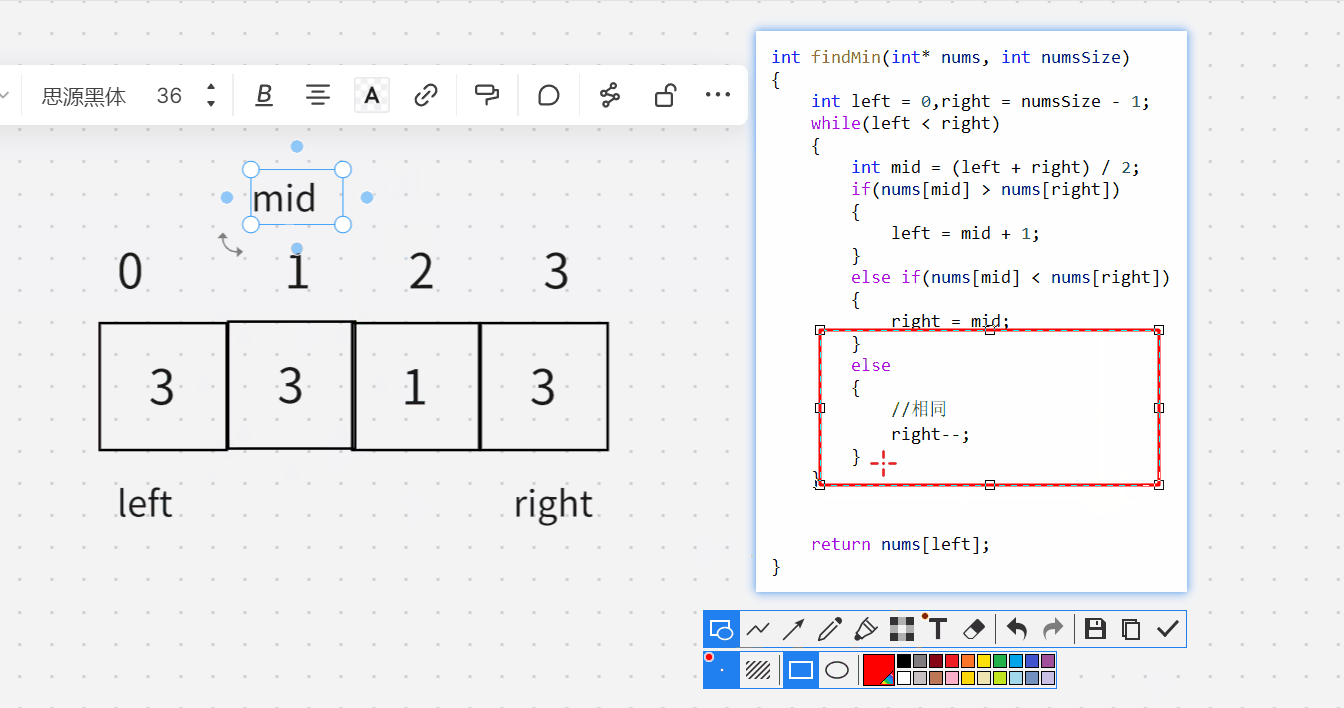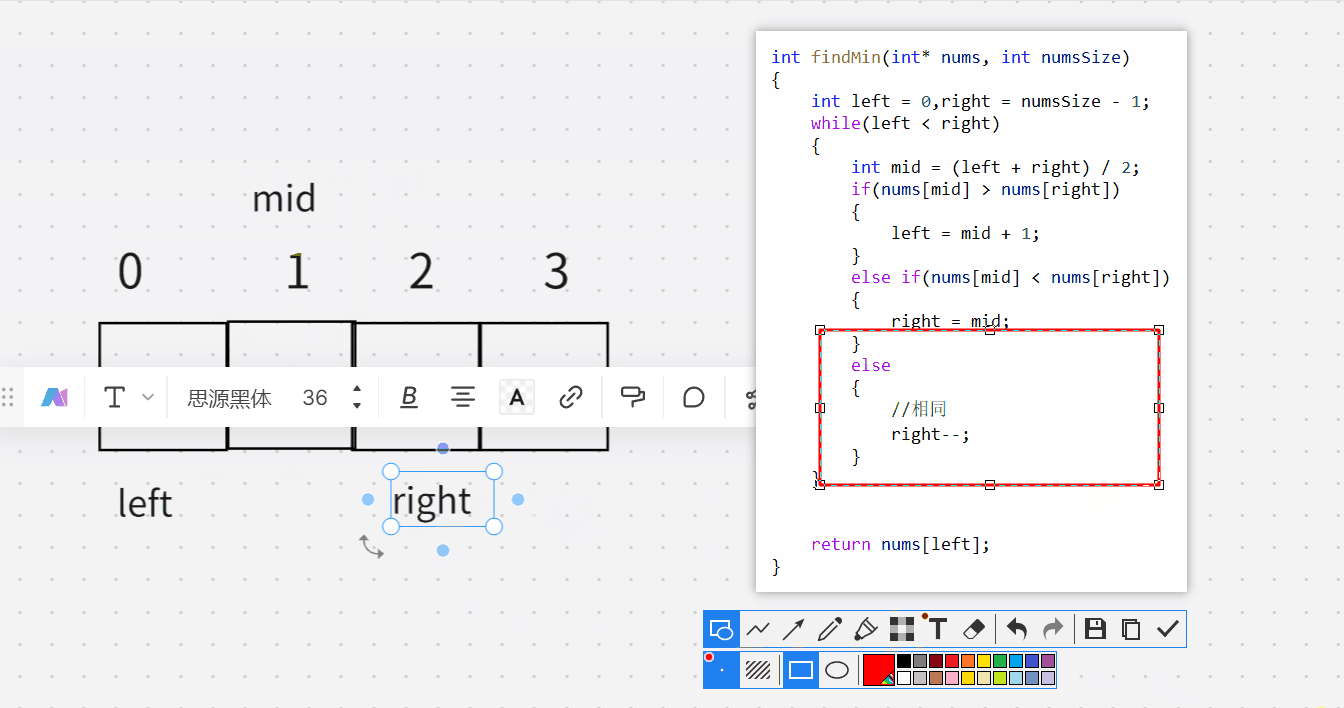
int findMin(int* nums, int numsSize)
{
int left = 0,right = numsSize - 1;
while(left < right)
{
int mid = (left + right) / 2;
if(nums[mid] > nums[right])
{
left = mid + 1;
}
else if(nums[mid] < nums[right])
{
right = mid;
}
else
{
//相同
right--;
}
}
return nums[left];
}
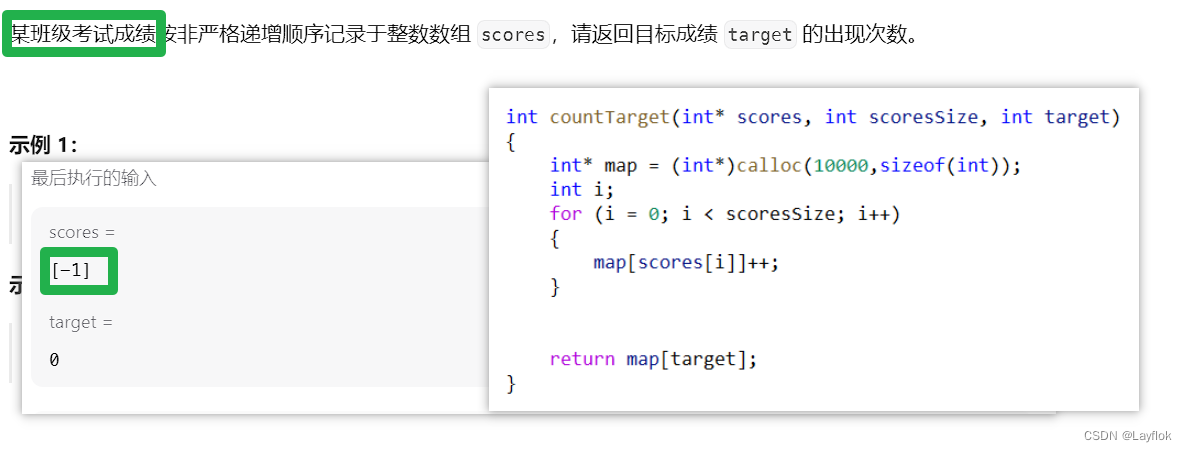
20.LCR.统计目标成绩出现的次数

没得说,没得说,我刚开始想的哈希表,直接做出来,然后再写二分的办法,结果出来了个这。
我笑了哈哈哈,-1分,可以可以。我抗不了.
这道题,可以用哈希表,暴力,双指针都可以,我这边是使用的二分法
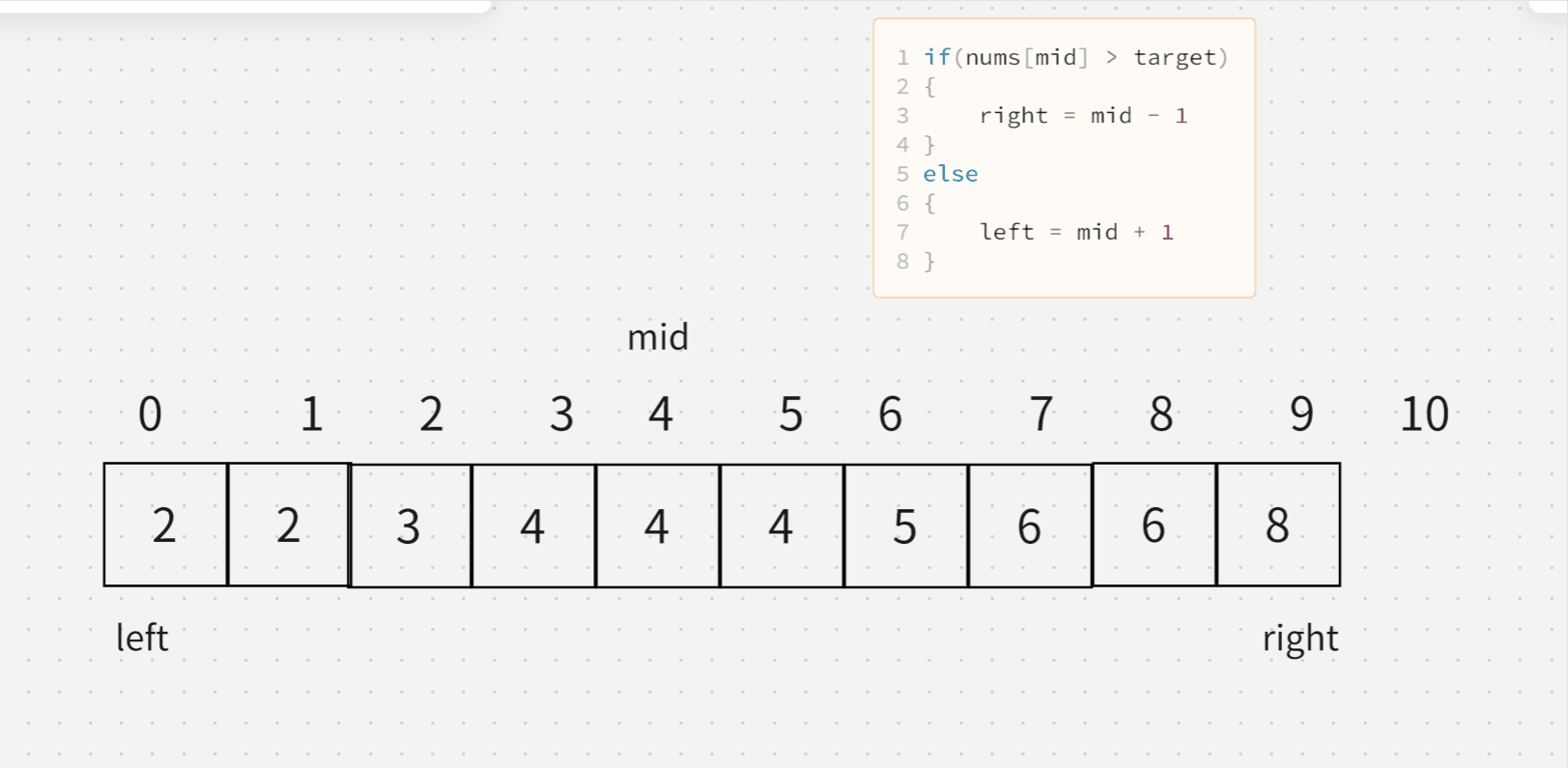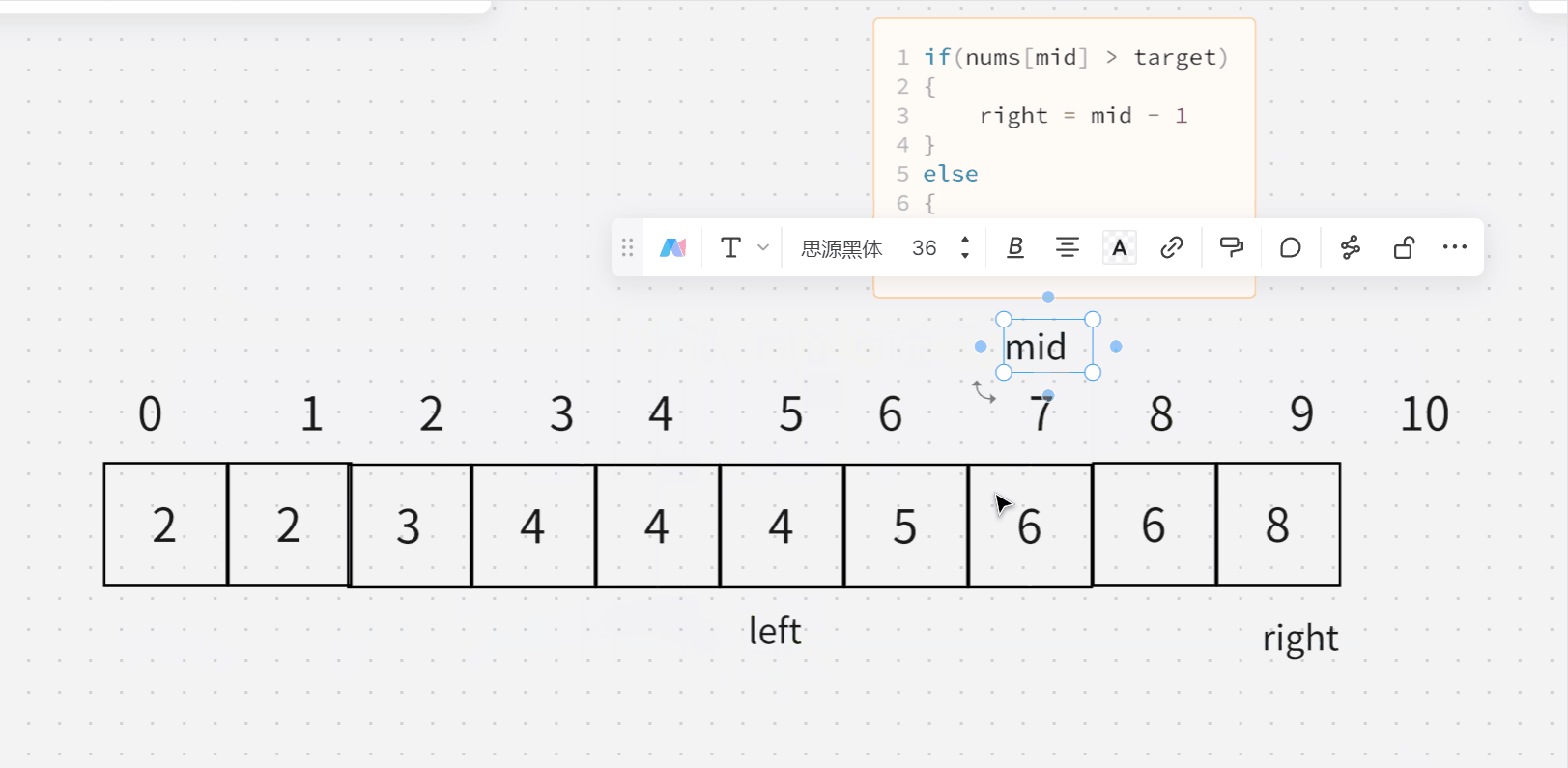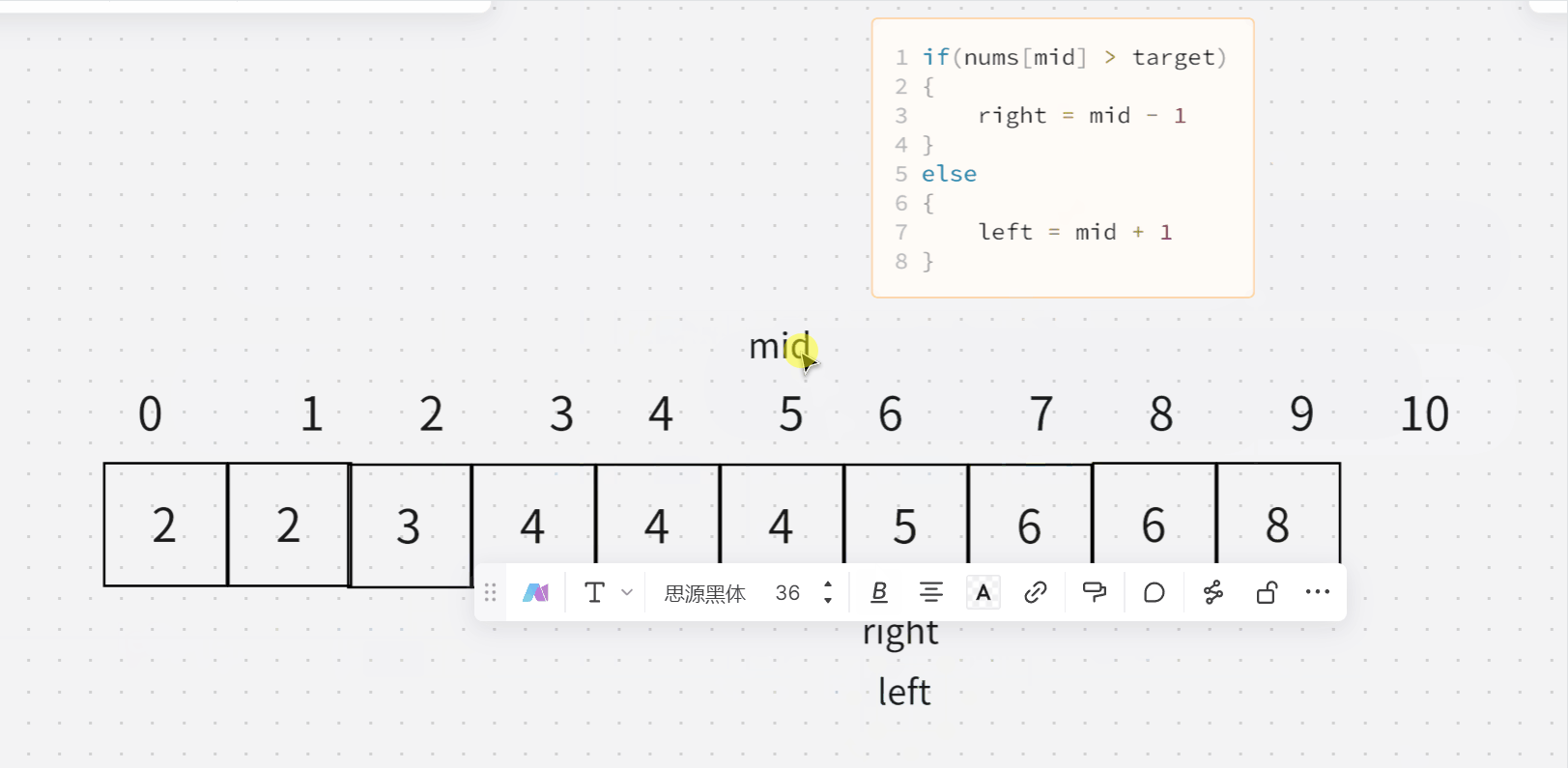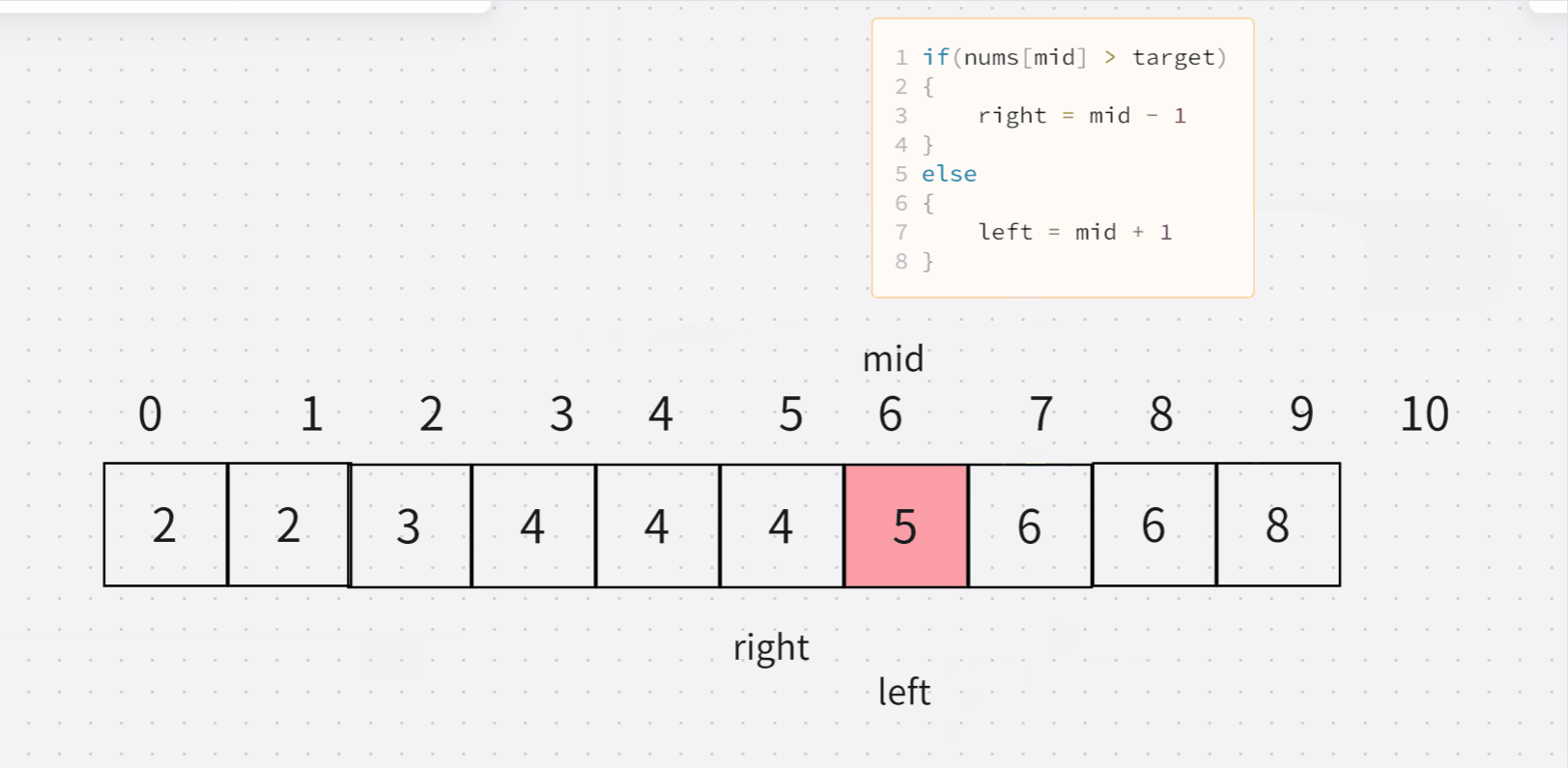
- 这道题的二分法,还不太一样,需要分别求出左边的起始位置和右边的结束位置。
- 先学会分别求左边和右边。
下图最后返回的下标是 3
右边,要注意右边返回的不是下标,而是所对应的前一个下标,所以最后还得减去1
- 当会找左边和右边的位置时候,它还是有序的,他俩相减就是长度,也就是次数
可以看出,二分查找,才是里面最关键的一环
int countTarget(int* scores, int scoresSize, int target)
{
int leftIndex = BinarySearch(scores,scoresSize,target,true);
int rightIndex = BinarySearch(scores,scoresSize,target,false) - 1;
if(leftIndex == rightIndex)
{ //同一个位置,就是1次呗
return 1;
}
return rightIndex - leftIndex + 1;
}
我用flag标识找左边还是找右边。
//flag == true 表示找最右边的target
//flag == false 表示找最左边的 target
int BinarySearch(int* nums,int numsSize,int target, bool flag)
{
int left = 0, right = numsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if((flag && nums[mid] >= target) || (!flag) && nums[mid] > target)
{
right = mid - 1;
}
else
{
left = mid + 1;
}
}
return left;
}
21.LCR.点名

- 如果records[mid] == mid, 说明至此之前的顺序肯定是对的,并没有缺失
- 如果records[mid] != mid ,说明至此之肯定有顺序是错的,已经缺失或者正好就是自己
int takeAttendance(int* records, int recordsSize)
{
int left = 0, right = recordsSize - 1;
while(left <= right)
{
int mid = (left + right) / 2;
if(records[mid] == mid)
{
left = mid + 1;
}
else
{
right = mid - 1;
}
}
return left;
}
22.LCR.查找总价格为目标值的两个商品

- 这道题与前面的题类似,甚至更简单。
int BinarySearch(int* nums, int left, int right,int target)
{
while(left <= right)
{
int mid = (left + right) / 2;
if(nums[mid] > target)
{
right = mid - 1;
}
else if(nums[mid] < target)
{
left = mid + 1;
}
else
{
return target;
}
}
return -1;
}
int* twoSum(int* price, int priceSize, int target, int* returnSize)
{
int* ans = (int*)malloc(sizeof(int) * 2);
*returnSize = 2;
int i;
for (i = 0; i < priceSize; i++)
{
int val = BinarySearch(price,i + 1,priceSize - 1,target - price[i]);
if(val != -1)
{
ans[0] = price[i];
ans[1] = val;
return ans;
}
}
return ans;
}
23.魔术索引

- 这道题,在一个循环里的一般的二分法,肯定是不行的,看完下面图片,
- 全部都是nums[mid] > mid。
- 但是答案确实两个极端
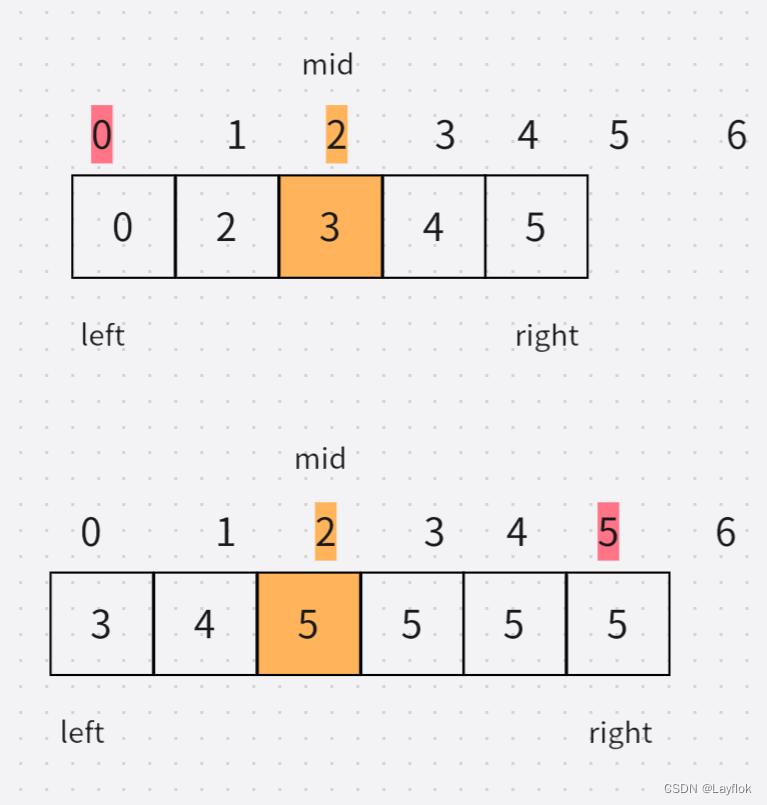
- 所以一般的while循环方式肯定是不行的,接下来就得采取递归的方式,进行二分。
- 运用递归的方式,在前面的数组转二叉搜索树中做过,很类似的递归方式,只是停止的条件不一致。
- 知道左边是[left,mid-1] 右边是[mid+1,right]ok了
- 然后拿一个index用来记录nums[mid]是否等于 mid 如果找到了的话,就使index = mid就好了
- 要注意,判断nums[mid] 是否等于mid 需要先将左边遍历到底后,再去进行,比如下张图,当第一次计算即可算出3合适,但是2也合适,它比3小,所以返回3肯定是错的

void BinarySearch(int* nums, int left, int right,int* index)
{
if(left > right)
{
return;
}
int mid = (right + left) / 2;
BinarySearch(nums,left, mid - 1,index);
if(*index != -1)
{
return;
}
if(nums[mid] == mid)
{
*index = mid;
return;
}
BinarySearch(nums,mid + 1, right,index);
}
int findMagicIndex(int* nums, int numsSize)
{
int index = -1;
BinarySearch(nums,0,numsSize - 1,&index);
return index;
}



![[GXYCTF2019]Ping Ping Ping](https://img-blog.csdnimg.cn/img_convert/284afcfc6b9c9e40b1745d677c7d75f6.png)