在快速发展的人工智能领域中，以高效和有效的方式使用大型语言模型（LLM）变得越来越重要。在本文中，您将学习如何以计算高效的方式使用低秩适应（LoRA）对LLM进行调整！

为什么需要微调？

预训练的大型语言模型通常被视为基础模型，原因很充分：它们在各种任务上表现良好，我们可以将它们作为基础来对特定任务进行微调。正如我们在前一篇文章中讨论的（一文读懂大型语言模型参数高效微调：Prefix Tuning与LLaMA-Adapter），我们讨论了微调使我们能够将模型适应于目标领域和目标任务。但这可能在计算上非常昂贵 —— 模型越大，更新其层的成本就越高。

作为更新所有层的替代方案，已经开发出了如前缀调整和适配器等参数高效的方法。现在，还有一种流行的参数高效微调技术：低秩适应（LoRA）由Hu等人提出。什么是LoRA？它是如何工作的？它与其他流行的微调方法相比如何？让我们在这篇文章中回答所有这些问题！

使权重更新更加高效

基于上述思想，论文《LoRA：大型语言模型的低秩适应》提出将权重变化 ΔW 分解为低秩表示。 （为了技术上的准确性，LoRA 并不直接分解矩阵，而是通过反向传播学习分解后的矩阵 —— 这是一个细微的细节，稍后将会有所说明）。

在我们仔细研究 LoRA 之前，让我们简要地解释一下常规微调期间的训练过程。那么，权重变化 ΔW 是什么呢？假设 W 代表给定神经网络层中的权重矩阵。然后，使用常规反向传播，我们可以得到权重更新 ΔW，它通常计算为损失的负梯度乘以学习率：

ΔW = α ( -∇ LW)。

接着，当我们有了 ΔW，我们可以按照以下方式更新原始权重：W' = W + ΔW。这在下图中有所说明（为简单起见省略了偏置向量）：

或者，我们可以将权重更新矩阵保持独立，并按照以下方式计算输出：h = W x + ΔW x，

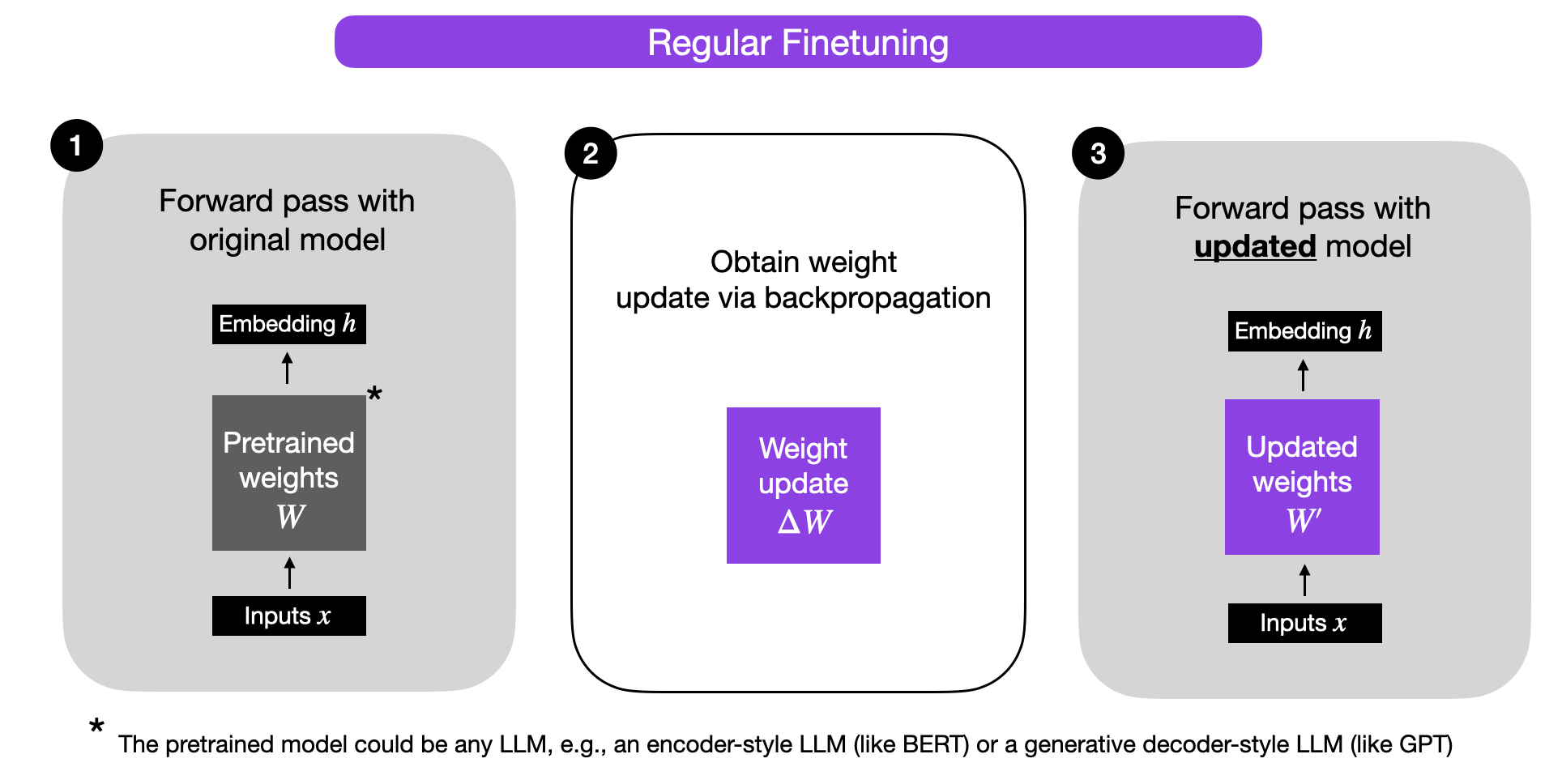
x代表的是输入，如下图所示：

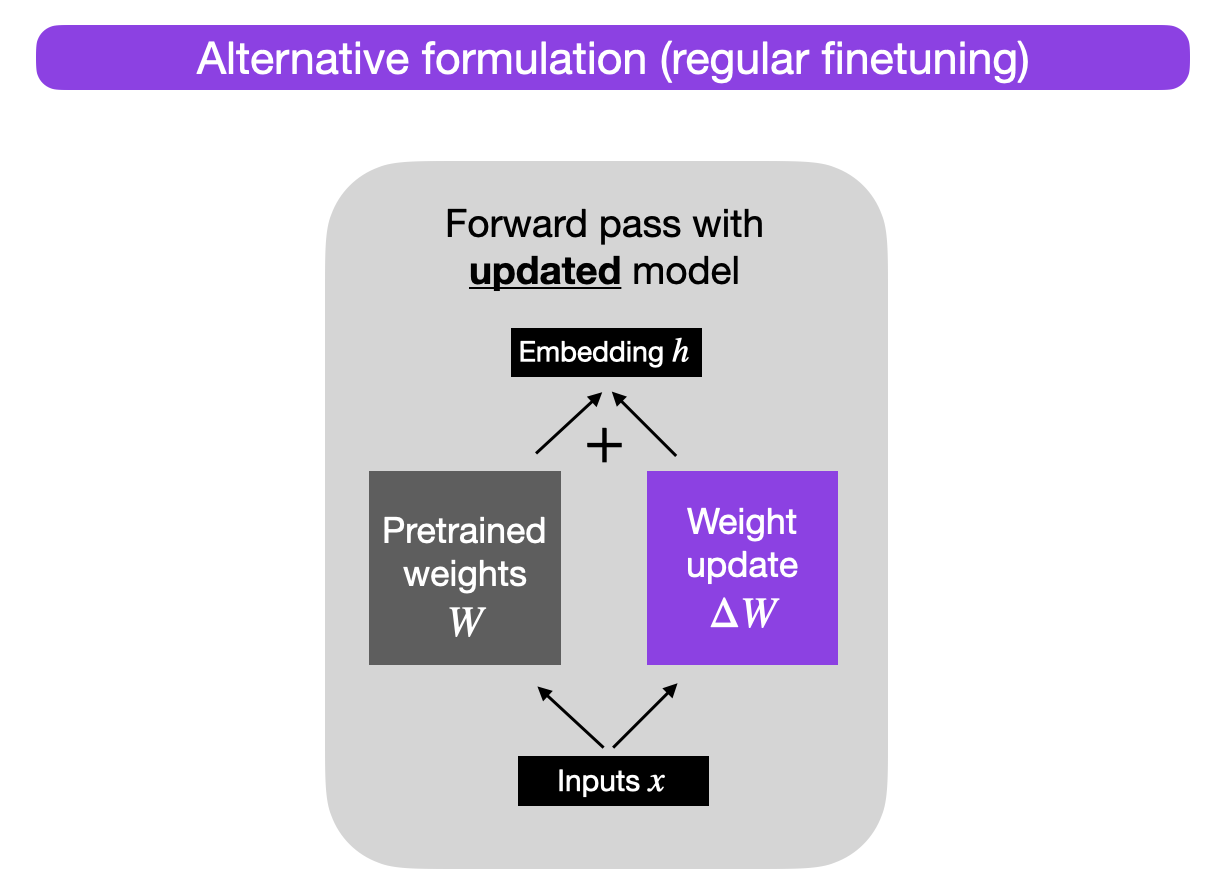
为什么要这么做？目前，这种替代性的表述用于教学目的，以便说明 LoRA，但我们稍后会回到这一点。

因此，当我们训练神经网络中的全连接（即“密集”）层时，如上所示，权重矩阵通常具有满秩，这是一个技术术语，意味着矩阵没有任何线性相关（即“冗余”）的行或列。与满秩相反，低秩意味着矩阵具有冗余的行或列。

因此，虽然预训练模型的权重在预训练任务上是满秩的，但 LoRA 的作者指出，根据 Aghajanyan 等人（2020）的研究，预训练的大型语言模型在适应新任务时具有低“内在维度”。

低内在维度意味着数据可以通过较低维度的空间有效表示或近似，同时保留其大部分基本信息或结构。换句话说，这意味着我们可以将适应任务的新权重矩阵分解为低维（更小）的矩阵，而不会丢失太多重要信息。

例如，假设 ΔW 是 A × B 权重矩阵的权重更新。然后，我们可以将权重更新矩阵分解为两个较小的矩阵：ΔW = WA WB，其中 WA 是一个 A × r 维矩阵，WB 是一个 r × B 维矩阵。在这里，我们保持原始权重 W 不变，只训练新矩阵 WA 和 WB。简而言之，这就是 LoRA 方法，如下图所示。

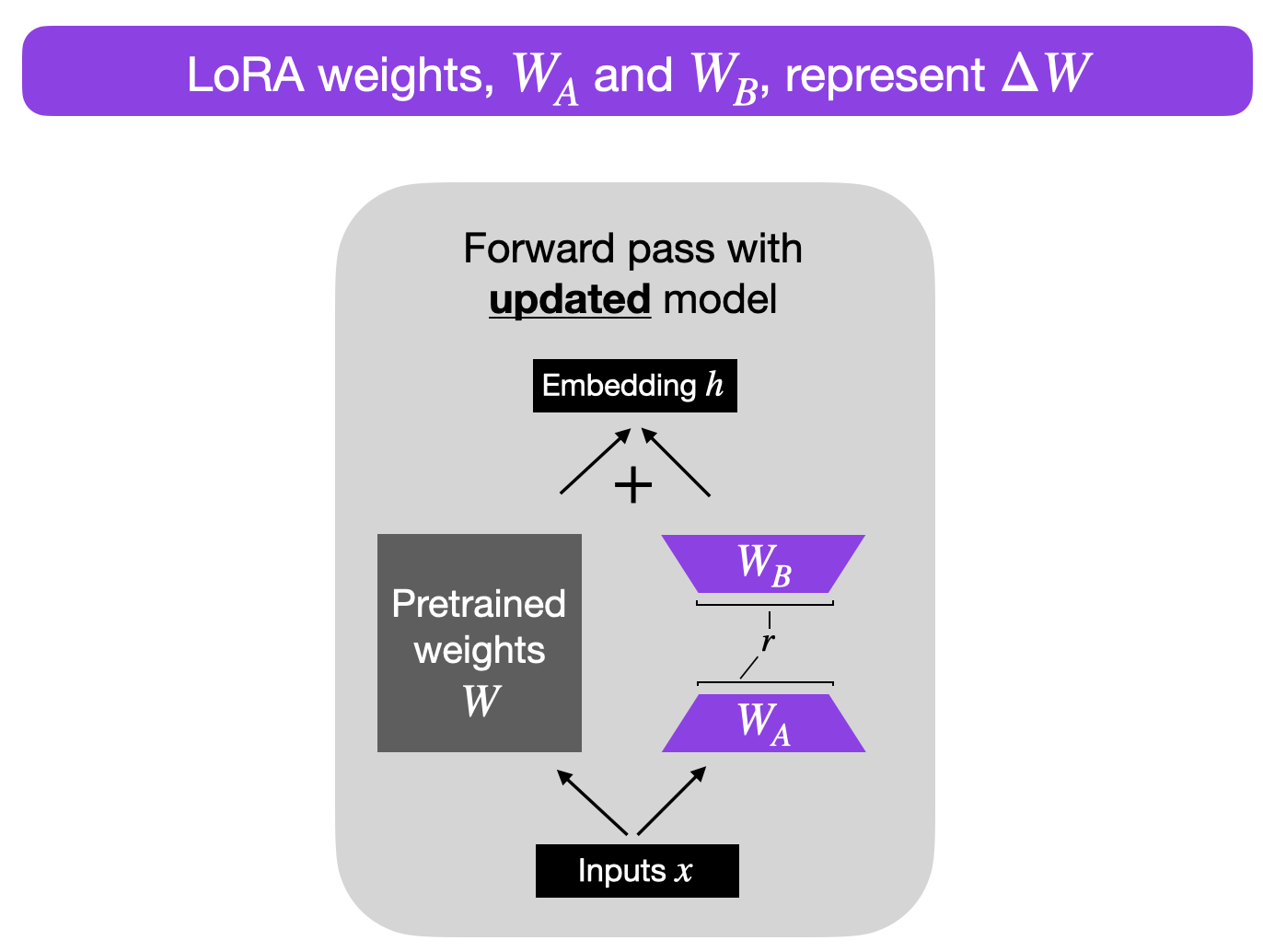
选择秩

请注意，在上面的图中，r 是一个超参数，我们可以用它来指定用于适应的低秩矩阵的秩。较小的 r 会导致更简单的低秩矩阵，这意味着在适应过程中需要学习的参数更少。这可以导致更快的训练和潜在的计算需求减少。然而，使用较小的 r，低秩矩阵捕获任务特定信息的能力会降低。这可能导致适应质量降低，模型在新任务上的表现可能不如使用更高的 r。总之，在 LoRA 中选择较小的 r 有一个折中的选择，涉及模型复杂性、适应能力以及欠拟合或过拟合的风险。因此，尝试不同的 r 值以找到实现新任务所需性能的正确平衡是很重要的。

实现 LoRA

LoRA 的实现相对简单。我们可以将其视为 LLM 中全连接层的修改后的前向传播。用伪代码表示，它看起来如下所示：

input_dim = 768  # e.g., the hidden size of the pre-trained model
output_dim = 768  # e.g., the output size of the layer
rank = 8  # The rank 'r' for the low-rank adaptation

W = ... # from pretrained network with shape input_dim x output_dim

W_A = nn.Parameter(torch.empty(input_dim, rank)) # LoRA weight A
W_B = nn.Parameter(torch.empty(rank, output_dim)) # LoRA weight B

# Initialization of LoRA weights
nn.init.kaiming_uniform_(W_A, a=math.sqrt(5))
nn.init.zeros_(W_B)

def regular_forward_matmul(x, W):
    h = x @ W
return h

def lora_forward_matmul(x, W, W_A, W_B):
    h = x @ W  # regular matrix multiplication
    h += x @ (W_A @ W_B)*alpha # use scaled LoRA weights
return h

在上述伪代码中，alpha 是一个调节组合结果（原始模型输出加上低秩适应）大小的缩放因子。这平衡了预训练模型的知识和新任务特定的适应 —— 默认情况下，alpha 通常设置为 1。另外请注意，虽然 WA 初始化为小的随机权重，但 WB 初始化为 0，因此ΔW = WA WB = 0 在训练开始时，意味着我们开始训练时使用原始权重。

参数效率

现在，让我们解决一个重要问题：如果我们引入新的权重矩阵，这怎么可能是参数高效的呢？新的矩阵 WA 和 WB 可以非常小。例如，假设 A=100 和 B=500，则 ΔW 的大小是 100 × 500 = 50,000。现在，如果我们将其分解为两个较小的矩阵，一个 100×5 维的矩阵 WA 和一个 5×500 维的矩阵 WB。这两个矩阵总共只有 5× 100 + 5 × 500 = 3,000 个参数。

减少推理开销

请注意，在实践中，如果我们像上面所示在训练后保持原始权重 W 和矩阵 WA 和 WB 分开，我们将在推理时产生小的效率损失，因为这引入了额外的计算步骤。相反，我们可以通过 W’ = W + WA WB 在训练后更新权重，类似于之前提到的 W’ = W + ΔW。

然而，在保持权重矩阵 WA 和 WB 分开的情况下也有实际优势。例如，假设我们想保留我们的预训练模型作为各个客户的基础模型，并希望从基础模型开始为每个客户创建一个微调的 LLM。在这种情况下，我们不需要为每个客户存储完整的权重矩阵 W’，而存储所有权重 W’ = W + WA WB 的模型对于 LLM 来说可能非常大，因为 LLM 通常有数十亿到数万亿的权重参数。因此，我们可以保留原始模型 W 并只需要存储新的轻量级矩阵 WA 和 WB。

用具体数字来说明这一点，一个完整的 7B LLaMA 检查点需要 23 GB 的存储容量，而如果我们选择 r=8 的秩，LoRA 权重可以小到 8 MB。

它在实践中有多好

LoRA 在实践中有多好，它与完全微调和其他参数高效方法相比如何？根据 LoRA 论文，使用 LoRA 的模型在多个任务特定基准测试中的建模性能略优于使用适配器、提示调整或前缀调整的模型。通常，LoRA 甚至比微调所有层的性能更好，如下面 LoRA 论文中带有注释的表格所示。（ROUGE 是评估语言翻译性能的指标，我在这里详细解释过。）

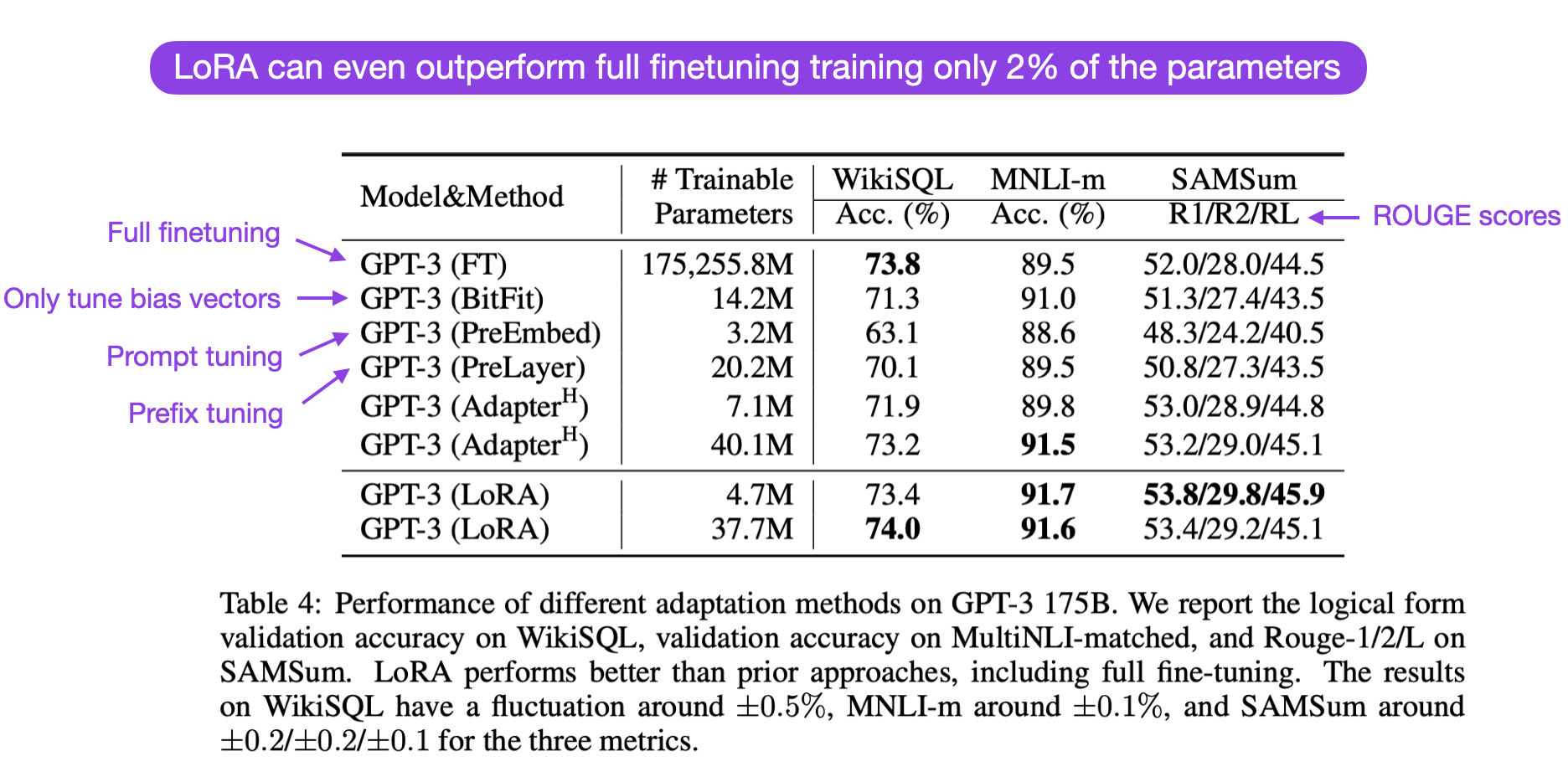
值得注意的是，LoRA 与其他微调方法是正交的，这意味着它也可以与前缀调整和适配器等方法结合使用。

LoRA 和 LLaMA

现在，让我们使用 LoRA 实现对 Meta 流行的 LLaMA 模型的微调。由于这已经是一篇很长的文章，我将避免在本文中包含详细的代码，但我建议查看 Lit-LLaMA 仓库，这是 Meta 流行的 LLaMA 模型的一个简单、易读的重新实现。 除了用于训练和运行 LLaMA 本身的代码（使用原始 Meta LLaMA 权重），它还包含使用 LLaMA-Adapter和 LoRA 微调 LLaMA 的代码。 要开始使用，我推荐以下操作指南：

1. 下载预训练权重 [ download_weights.md ]
2. 使用 LoRA 微调 [ finetune_lora.md ]
3. 使用适配器微调 [ finetune_adapter.md ]（可选，用于比较研究） 在下一节中，我们将比较 7B LLaMA 基础模型与使用 LoRA 和 LLaMA-适配器微调的 7B LLaMA 基础模型。（请注意，这需要至少 24 GB RAM 的 GPU）。（有关 LLaMA-适配器方法的更多详细信息，请参阅我之前的文章）

计算性能基准测试 在本节中，我们将比较 LLaMA 7B 基础模型与使用 LoRA 和 LLaMA-适配器微调的基础模型的计算性能。 微调数据集是此处描述的 Alpaca 52k 指令数据集，其结构如下：

数据集本身是按照《Self-Instruct》论文中描述的方法生成的，包含49,759个训练样例和2000个验证样例。Self-Instruct程序可以概括为4个步骤：

这是如何工作的？简而言之，它是一个四步过程：

1. 使用一组人类编写的指令（本例中为175条）填充任务池，并抽取指令样本。

2. 使用预训练的LLM（如GPT-3）确定任务类别。

3. 根据新指令，让预训练的LLM生成响应。

4. 收集、剪辑和过滤响应，然后将其添加到任务池中。

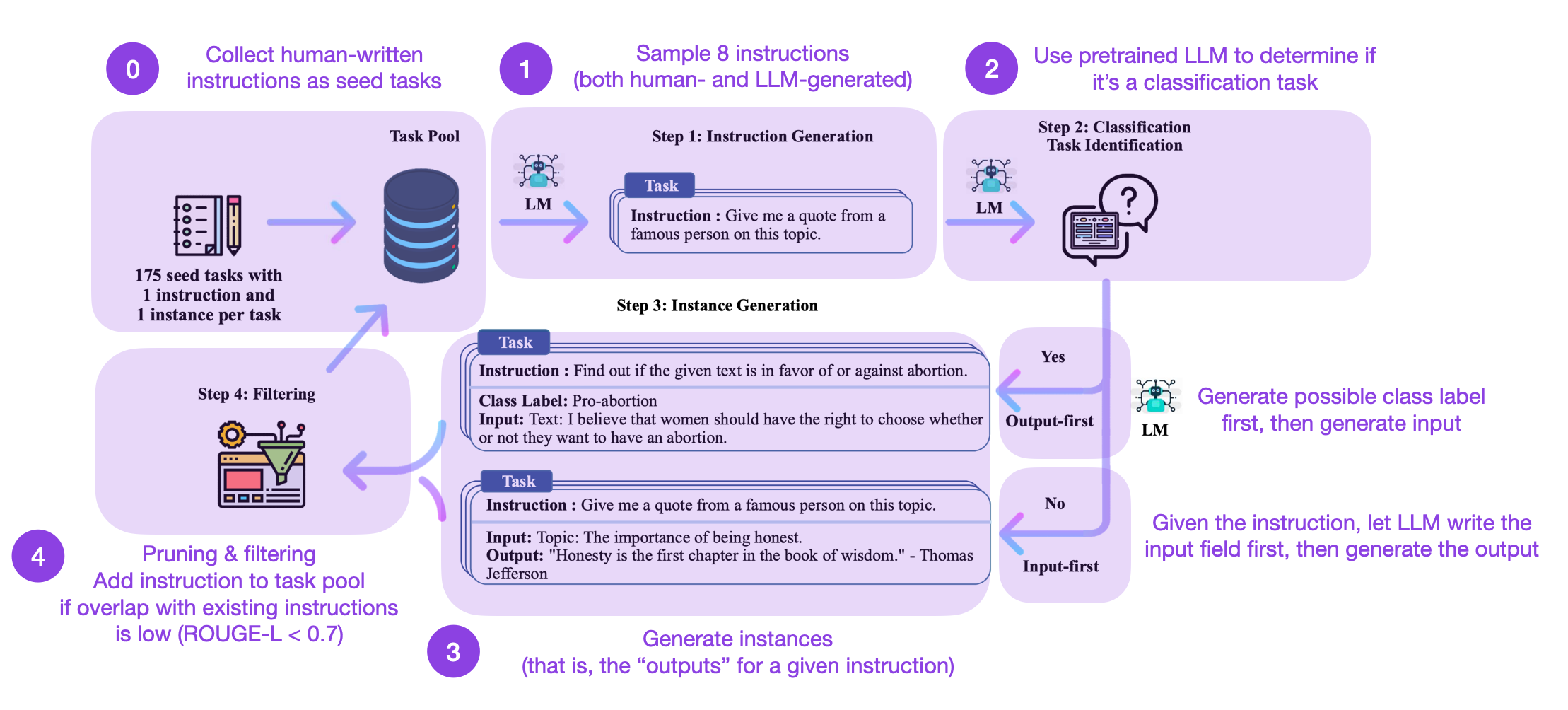
请注意，Alpaca 52k 数据集是使用上述自动自指导程序收集的。然而，你也可以使用（或与之比较）另一个数据集。例如，一个有趣的候选数据集是近期发布的开源 databricks-dolly-15k 数据集，该数据集包含约15k条由 Databricks 员工编写的指令/响应微调记录。如果您想使用 Dolly 15k 数据集而不是 Alpaca 52k 数据集，Lit-LLaMA 仓库包含了一个数据准备脚本。

考虑到以下超参数设置（块大小、批次大小和 LoRA r），适配器和 LoRA 都可以在单个具有24 Gb RAM的GPU上使用 bfloat-16 混合精度训练对7B参数的 LLaMA 基础模型进行微调。

LoRA

learning_rate = 3e-4
batch_size = 128
micro_batch_size = 4
gradient_accumulation_steps = batch_size // micro_batch_size
epoch_size = 50000 # train dataset size
num_epochs = 5
max_iters = num_epochs * epoch_size // micro_batch_size // devices
weight_decay = 0.0
block_size = 512
lora_r = 8
lora_alpha = 16
lora_dropout = 0.05
warmup_steps = 100

LaMA Adapter

learning_rate = 9e-3
batch_size = 128 / devices
micro_batch_size = 4
gradient_accumulation_steps = batch_size // micro_batch_size
epoch_size = 50000 # train dataset size
num_epochs = 5
max_iters = num_epochs * epoch_size // micro_batch_size // devices
weight_decay = 0.02
block_size = 512
warmup_steps = epoch_size * 2 // micro_batch_size // devices

鉴于代码未来可能会发生变化，在这里提供了 GitHub 上的代码（包括超参数设置）。

适配器大约使用了22 GB内存，在A100上完成了62,400次迭代，耗时162分钟。LoRA使用了21 GB内存，耗时192分钟。总的来说，根据 Lit-LLaMA 的实现，适配器和 LoRA 使用大致相同的内存量，并且训练时间大致相同。（请注意，这是在单个 GPU 上的情况，但如果您有多个 GPU，只需将设备参数改为 > 1 即可利用额外的加速！）

作为比较，完全微调（LLaMA 7B 包括32个变压器块和3个全连接输出层）至少需要2个GPU，每个至少30 GB，并进行完全分片训练以分配权重。或者，您可以使用4个 GPU，每个 GPU 的最大内存使用量为22 GB。4个 GPU 上的训练耗时1956分钟。在单个 GPU 上，这将至少需要6,000分钟，这比参数高效的LLaMA-适配器或 LoRA 替代方案贵30-40倍。

接下来，让我们看看应用不同微调策略后的模型输出。

评估建模性能

评估 LLM 生成的文本有几种指标。例如，困惑度、BLEU 和 ROUGE 得分是自然语言处理中用于评估 LLM 在各种任务上性能的一些最常用评估指标。然而，所有这些指标都有显著的缺陷，人类评估仍然是黄金标准——人类评估的缺点是它们昂贵且难以自动化。鉴于这已经是一篇很长的文章，我将避免详细讨论模型评估方法，并将其推迟到将来的一篇单独的文章中。在这篇未来的文章中，我们将研究不同的问答数据集。因此，为简单起见，我们将只关注下面的定性模型比较，看看不同模型生成的一些输出。

定性比较

为了定性地比较这些模型，我们将使用提示：“请解释权重衰减是如何工作的”。
Base model

$ python generate.py \
--checkpoint_path checkpoints/lit-llama/7B/lit-llama.pth

“请解释权重衰减是如何工作的……以及为什么有时它似乎有效，有时又不行！用最简单的术语来说，权重衰减从模型中移除特征（作为它们重要性的函数）。这也被称为正则化。”

正如我们所见，模型开始继续提示，添加“……为什么有时它似乎有效，有时又不行！”这是因为基础模型只在下一个词预测任务上进行了训练，没有特别针对遵循指令进行训练。尽管如此，它在下文中尝试了解释。这个解释对正则化总体上做了一些正确的陈述，但它并没有真正抓住权重衰减的关键机制。

LLaMA-Adapter

$ python generate_adapter.py \
--adapter_path out/adapter/alpaca/lit-llama-adapter-finetuned.pth \
--pretrained_path checkpoints/lit-llama/7B/lit-llama.pth

“权重衰减是一种用于对词数进行惩罚的方法。通过选择词数较少的句子，模型更有可能选择这些句子，这可能提供重要信息。”

这个解释在语法上是合理的，但它并不一定是我们正在寻找的内容。

LoRA

$ python generate_lora.py \
--lora_path out/lora/alpaca/lit-llama-lora-finetuned.pth \
--pretrained_path checkpoints/lit-llama/7B/lit-llama.pth

“权重衰减是机器学习模型中用于减少过拟合的算法参数。它是一个过程，通过调整模型的权重来减少模型中不太重要特征的影响并防止过拟合。通过在权重中添加少量噪声来使用权重衰减，以减少模型对训练数据的影响。这个过程鼓励模型更多地关注对预测任务更重要的特征。”

当我们考虑到广义线性模型时，这个解释是有意义的，我们迫使模型学习较小的权重参数，这些参数与输入特征相乘。在神经网络中，这通常会应用于模型中的所有权重参数。

请注意，上面的 LoRA 方法目前使用了最多的内存。然而，我们可以通过将 LoRA 权重与预训练模型权重合并，如前所述，来减少这种内存使用。

这种定性概述只是展示了这些模型能力的一小部分，因为评估 LLM 本身就是一个大话题。但作为一个要点，在指令数据集上微调 LLM 时，LoRA 可以以相对成本效益的方式使用。

结论

在这篇文章中，我们讨论了低秩适应（LoRA），这是对全微调的一种参数高效替代方案。我们看到，使用 LoRA 在单个 GPU 上微调相对较大的模型（如 LLaMA）可以在几小时内完成，这对那些不想在 GPU 资源上花费数千美元的人来说特别有吸引力。特别好的是，我们可以选择性地将新的 LoRA 权重矩阵与原始的、预训练的权重合并，这样我们在推理过程中就不会产生额外的开销或复杂性。

随着越来越多的 ChatGPT 或 GPT-4 开源替代品的出现，针对特定目标数据集或目标的 LLM 微调和定制将在各种研究领域和行业中变得越来越有吸引力。像 LoRA 这样的参数高效微调技术使微调更加资源高效和易于访问。

了解原文：链接