采样定理，通常被称为奈奎斯特-香农采样定理，是信号处理中的一个基本原则。它解释了如何从连续信号中采样以便在后续能完全重构原始信号。以下是该定理的核心要点：

• 采样定理的陈述：
• 为了从其样本中无失真地重构一个连续时间信号，采样频率（采样率）必须至少是信号中最高频率成分的两倍。这个最低的采样频率被称为“奈奎斯特频率”。
• 为什么需要奈奎斯特频率：
• 如果采样频率低于信号最高频率的两倍，就会发生**“混叠”现象**。混叠是指高频信号在低采样率下被错误地解释为低频信号，导致原始信号的失真。
• 实际应用：
• 在实际应用中，通常会选择略高于理论奈奎斯特频率的采样率，以确保信号能被准确重构，特别是当信号接近最高频率成分时。
• 例子：
• 假设一个信号包含的最高频率成分为 3000 Hz，那么根据采样定理，采样频率应至少为 6000 Hz（或6 kHz）。在实践中，可能会选择更高的采样率，例如 8000 Hz，来确保信号的准确重构。

实践一下

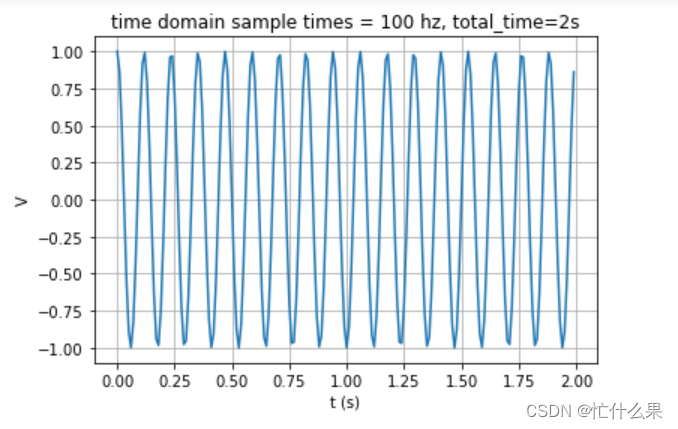
假设我们有个时域的连续信号cos(8.5t)，接下来要设置一个时间1秒，对它进行该时间内的信号采样，然后对其进行傅里叶变换到频域，频域得到的结果应该是在8.5hz有明显的突变。按照采样定理，我们应该设置大于8.52的采样频率，我们先设置1个低于8.52的采样频率10，反变换前后结果如下：
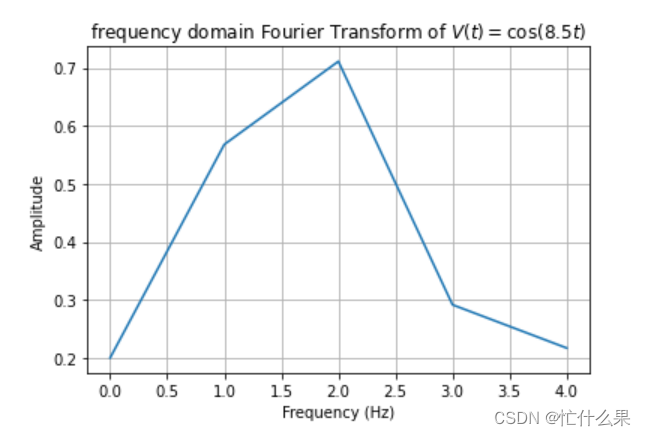频域结果在2HZ，与8.5hz完全不符，说明采样频率过低会导致频域结果完全失真。
再设置1个正好等于8.52的采样频率17，反变换前后结果如下：
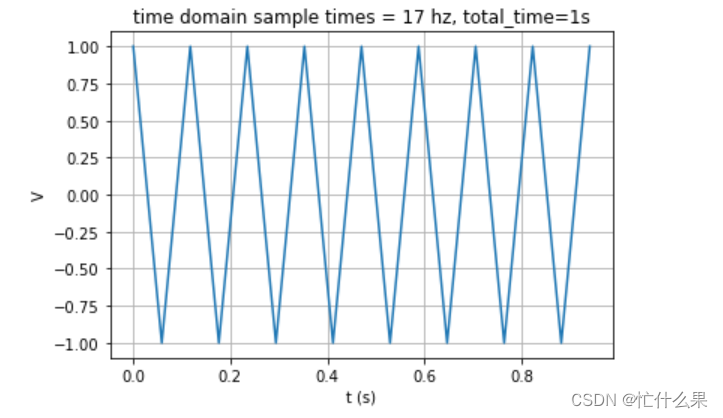
显示在7的位置，相比于之前靠近8.5了，但是还是不准确。
再设置1个稍微大于8.52的采样频率20，反变换前后结果如下：
显示在8的位置，相比于之前更靠近8.5了，但是还是不准确。
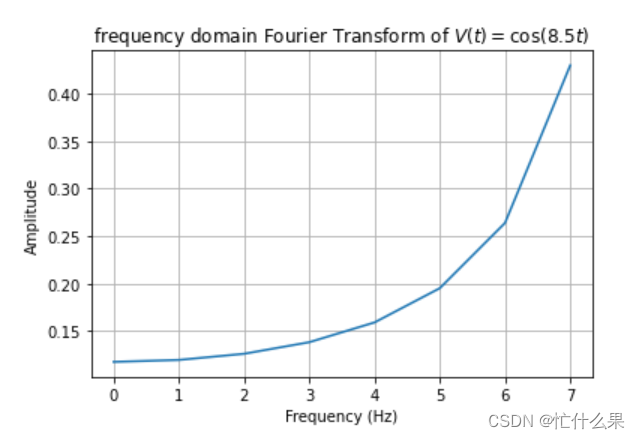
再设置1个大于8.5*2的采样频率50，反变换前后结果如下：
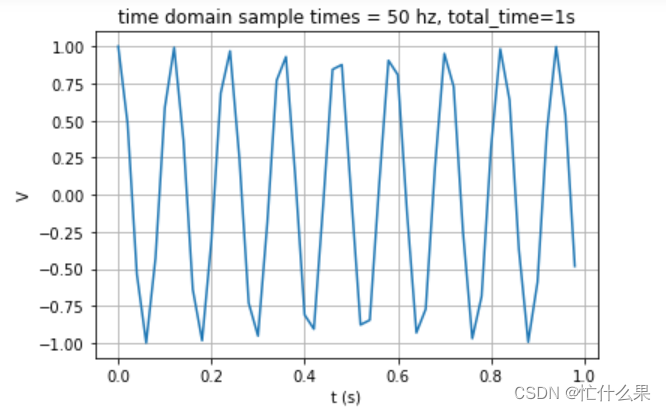
显示在9的位置，依旧靠近8.5了，但是还是不准确。此时将频率打印出来，[ 0. 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 12. 13. 14. 15. 16. 17. 18. 19. 20. 21. 22. 23. 24.]，没有8.5，所以继续加大采样频率，设置采样频率100。
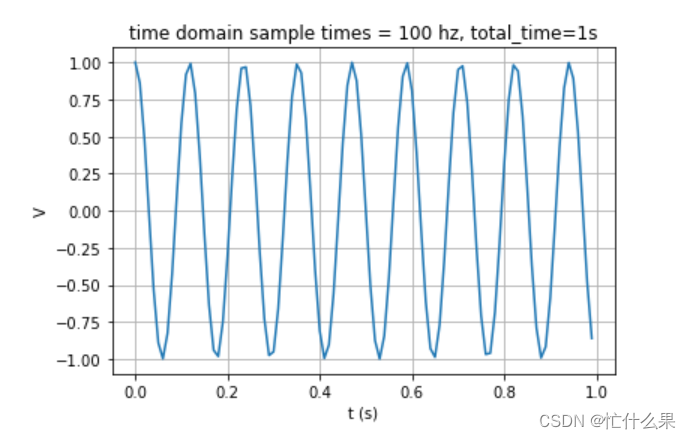
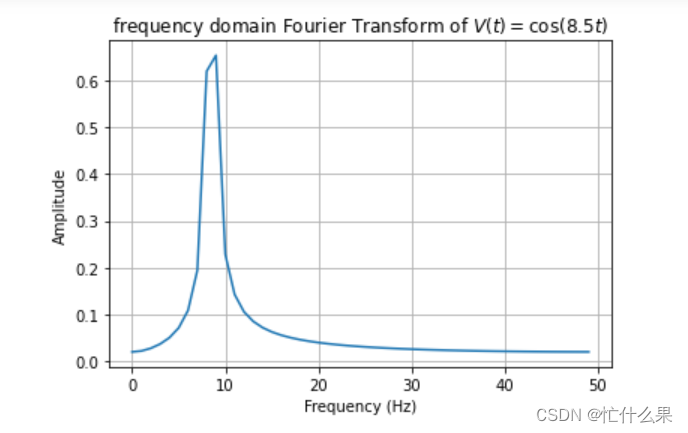此时出现一个分辨率问题。补充知识：

• 时域采样率决定了频域中可分辨的最大频率（奈奎斯特频率）

Fmax=时域采样频率ft（HZ）/2

• 频域的采样间隔（频率分辨率）取决于时域中信号的总持续时间 Tall

频率分辨率Δf=1/T_all

本例中我们设置的总时间T_all是1秒，100次采样，也就是ft=100，那

频率分辨率Δf=1/T_all=1/1=1
点数N=100*1=100
时间分辨率Δt=1/ft=1/100=0.01

频域的采样间隔只和总时间T_all有关。频率分辨率是1，所以不会出现8.5hz，所以我们设置总时间是2秒重新进行一次实验仿真。
此时

频率分辨率Δf=1/T_all=1/2=0.5
点数N=100*2=200
时间分辨率Δt=1/ft=1/100=0.01

先设置1个低于8.52的采样频率10，频率范围：[0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. ]
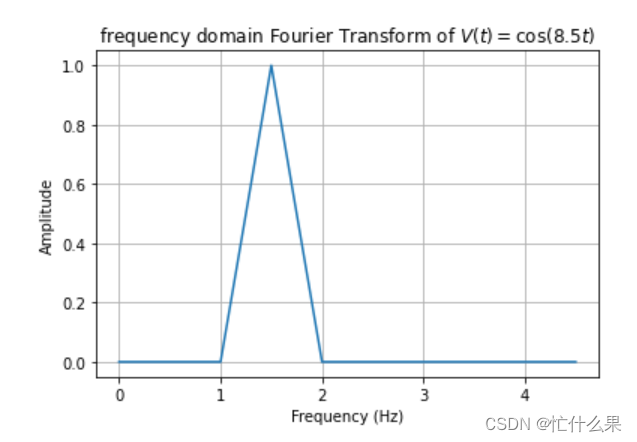然后设置1个等于8.52的采样频率17，频率范围：[0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. 8.5 9. 9.5]，可以看到这次8.5hz是准确的。
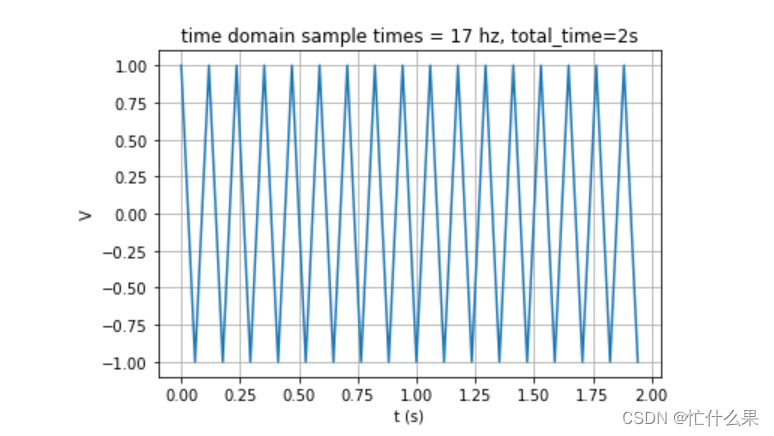
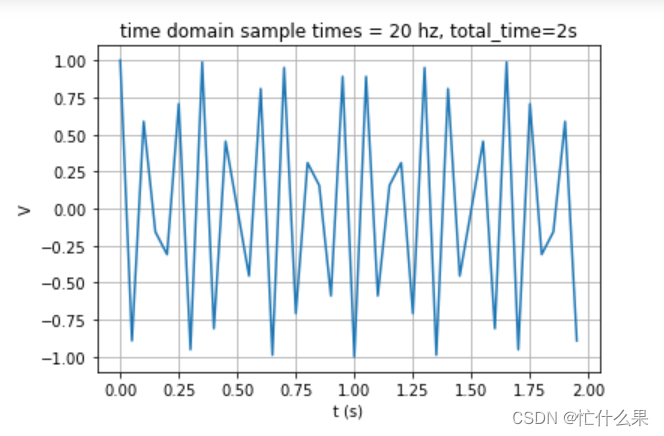
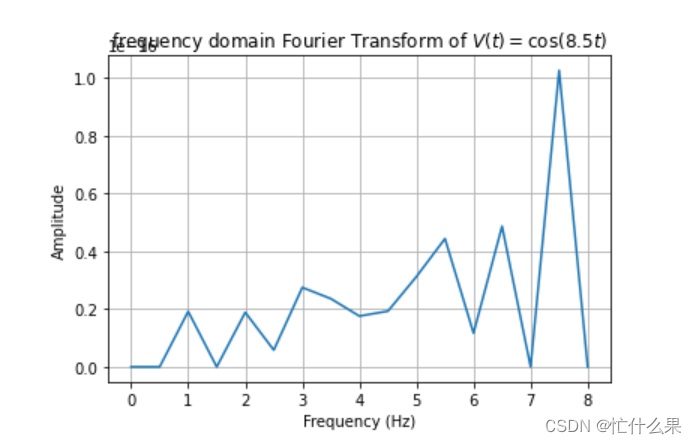然后设置1个略大于8.5*2的采样频率20，频率范围：[0. 0.5 1. 1.5 2. 2.5 3. 3.5 4. 4.5 5. 5.5 6. 6.5 7. 7.5 8. 8.5 9. 9.5]
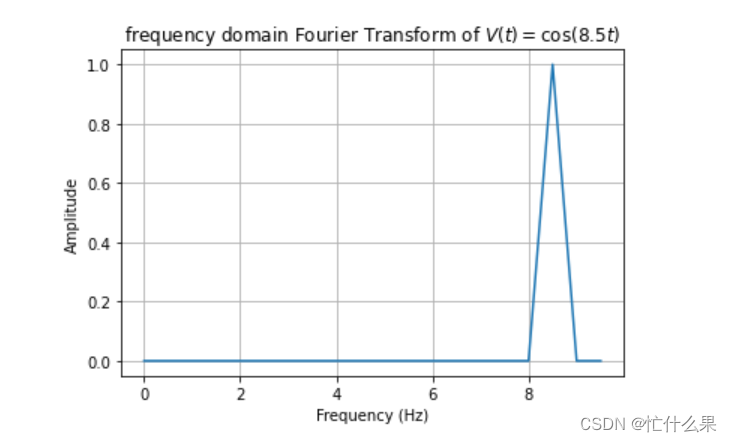再设置50hz，也能准确找到8.5HZ

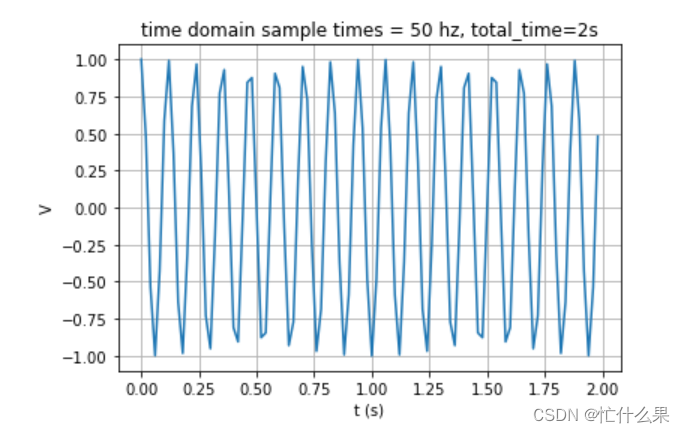
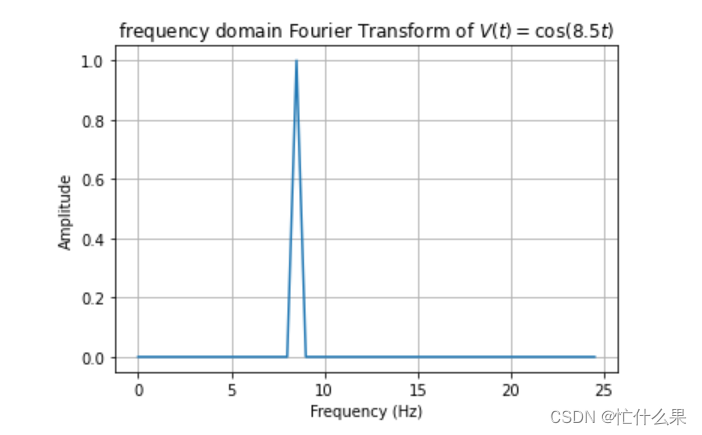再设置100hz，也能准确找到8.5HZ