.

个人主页：晓风飞
专栏：数据结构|Linux|C语言
路漫漫其修远兮，吾将上下而求索

---

---

引言

在数据结构和算法的世界中，排序是一个基本而重要的概念。堆排序是一种高效的排序算法，它利用堆这一数据结构的特性来实现。在这篇文章中，我们将深入探索堆排序的原理，并通过C语言示例来展示它的实现。

---

什么是堆？

堆是一种特殊的完全二叉树，其中每个父节点的值都大于或等于其子节点的值（最大堆），或者每个父节点的值都小于或等于其子节点的值（最小堆）。在堆排序中，我们通常使用最大堆。

---

建堆

升序：建大堆
降序：建小堆

---

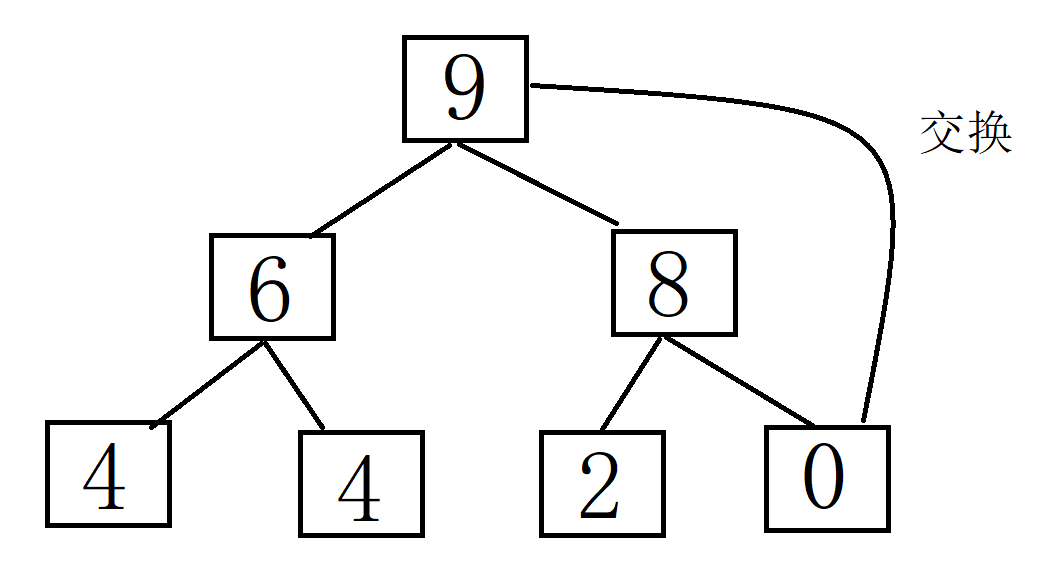
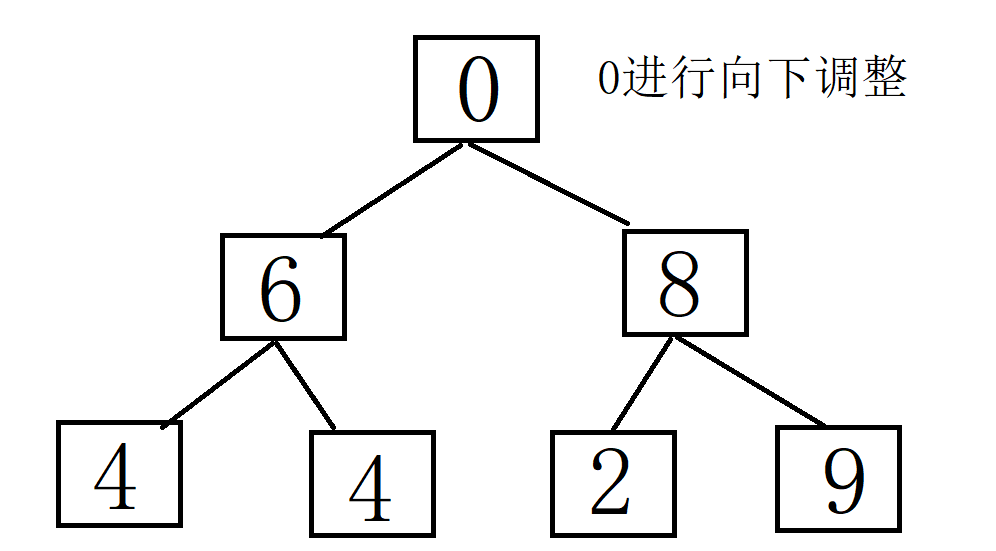
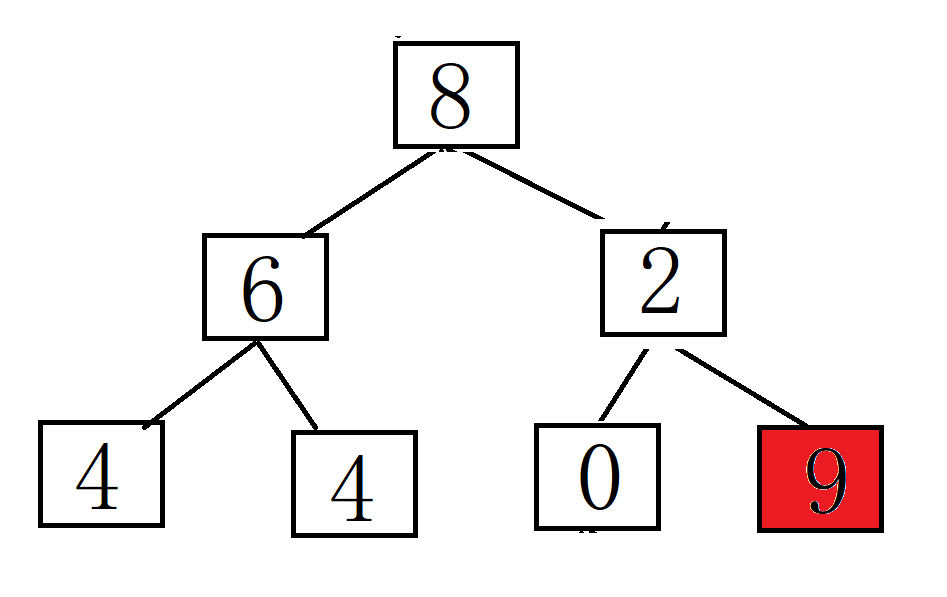
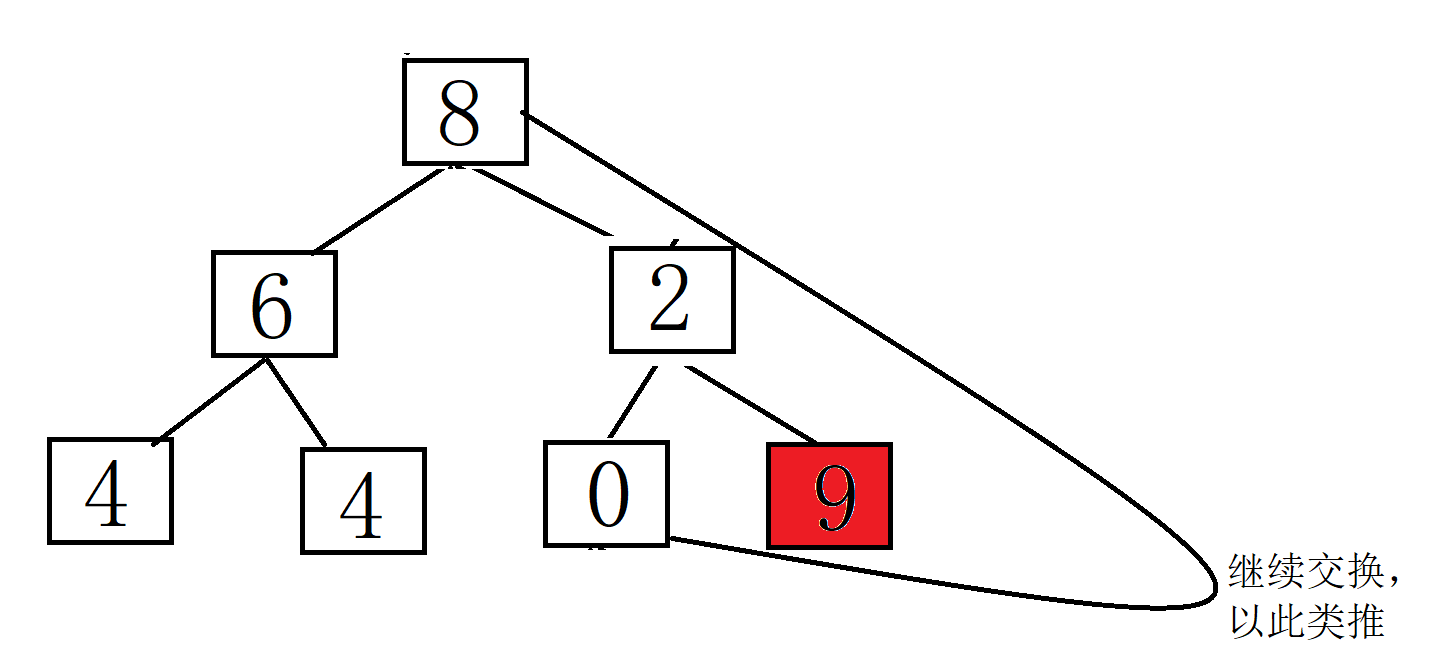
堆排序：

将堆顶元素（最大值）与最后一个元素交换，然后减少堆的大小，并重新对堆顶元素执行下沉操作。重复此过程，直到堆的大小为1。建堆和堆删除中都用到了向下调整，因此掌握了向下调整，就可以完成堆排序。
以下是使用实现堆排序的基本步骤：

排序的最终结果

---

堆排序实现

函数声明

交换函数 :
void Swap(HPDataType* p1, HPDataType* p2)
下沉调整 :
void DnAdd(HPDataType* a, HPDataType parent, int size)
堆排序函数:
void HeapSort(int* a, int n)

交换函数 Swap

void Swap(HPDataType* p1, HPDataType* p2) {
  HPDataType tmp = 0;  // 临时变量用于交换
  tmp = *p1;
  *p1 = *p2;
  *p2 = tmp;
}

Swap 函数的作用是交换两个元素的值。这在堆排序中非常重要，特别是在删除堆顶元素或重构堆的过程中。此函数通过传递指向数据的指针来直接修改原数组。

下沉调整 DnAdd

void DnAdd(HPDataType* a, HPDataType parent, int size) {
  int child = parent * 2 + 1; // 找到左子节点
  while (child < size) {
    // 检查右子节点是否存在,以及比较左右两个子节点的值
    if (child + 1 < size && a[child + 1] > a[child]) {
      child++; // 选择较大的子节点
    }
    // 如果子节点大于父节点，则需要交换
    if (a[child] > a[parent]) {
      Swap(&a[child], &a[parent]); // 交换父子节点
      parent = child; // 更新父节点位置
      child = parent * 2 + 1;
    } else {
      break; // 如果不需要交换，则终止循环
    }
  }
}

DnAdd 函数实现了堆的下沉调整，是构建和维护堆的关键操作。如果子节点的值大于父节点的值，则需要进行交换，以确保维护最大堆的性质。

堆排序函数 HeapSort

void HeapSort(int* a, int n) {
  // 构建初始大顶堆
  for (int i = (n / 2) - 1; i >= 0; i--) {
    DnAdd(a, i, n);
  }
  
  // 从堆中逐个移除元素并进行排序
  for (int end = n - 1; end > 0; end--) {
    Swap(&a[0], &a[end]); // 将最大的元素（堆顶）移动到数组的末尾
    DnAdd(a, 0, end); // 对剩余的堆进行向下调整
  }
}

HeapSort 函数首先通过调用 DnAdd 函数建立一个大顶堆。之后，通过不断移除堆顶元素（数组中的最大元素）并将其移动到数组的末尾，然后再次调用 DnAdd 函数进行下沉调整，最终达到整个数组的排序目的。

主函数

Copy code
int main() {
  int arr[] = { 8, 6, 4, 2, 0, 9, 4 };
  HeapSort(arr, sizeof(arr) / sizeof(arr[0]));
  for (int i = 0; i < sizeof(arr) / sizeof(arr[0]); i++) {
    printf("%d ", arr[i]);
  }
}

在主函数中，我们定义了一个未排序的数组 arr 并调用了 HeapSort 函数对其进行排序。排序完成后，使用一个循环来打印排序后的数组元素。通过main函数中的测试数组，我们可以看到HeapSort函数如何将无序数组转换成一个有序序列。我们也可以通过更换数组中的元素来测试不同的数据集。

---

文件中找TopK问题

什么是TOP-K问题

TOP-K问题是指在一个大数据集中找到前K个最大或最小的元素。这个问题在多个领域都非常常见，比如排名、选举、统计和游戏等。常见的例子包括找到考试成绩中的前10名、世界500强企业或者游戏中最活跃的100名玩家。

当数据量非常大时，简单的排序方法可能会因为数据量超过内存限制而变得不可行。此外，完整的排序操作的时间复杂度为
O(nlogn),这在数据量极大时效率低下。

堆排序的解决方案

堆排序提供了一个更为高效的解决方案，时间复杂度为O(nlogK)，这对于大数据集来说是一个巨大的提升。解决TOP-K问题的基本思路是：

用数据集合中前K个元素来建堆：
如果我们需要找到前K个最大的元素，则建立一个最小堆。
如果我们需要找到前K个最小的元素，则建立一个最大堆。
用剩余的N-K个元素依次与堆顶元素比较：
如果当前元素比堆顶元素大（在寻找最大元素时）或小（在寻找最小元素时），则将其与堆顶元素替换，并重新调整堆。
提取堆中的元素：

经过上述过程后，堆中剩余的K个元素就是我们要找的前K个最大或最小的元素。

操作应用

在文件中建立100000个数，查找前5个数最大的数

void PrintTopK(const char* file, int k)
{
  FILE* fout = fopen(file, "r");
  if (fout == NULL)
  {
    perror("fopen error");
    return;
  }


  // 建一个k个数的最小堆
  int* minheap = (int*)malloc(sizeof(int) * k);
  if (minheap == NULL)
  {
    perror("malloc error");
    fclose(fout); // 记得关闭文件指针
    return;
  }


  // 读取前k个数，以构建最小堆
  for (int i = 0; i < k; i++)
  {
    if (fscanf(fout, "%d", &minheap[i]) != 1) // 检查fscanf的返回值
    {
      perror("fscanf error");
      free(minheap);
      fclose(fout);
      return;
    }
    UpAdd(minheap, i); // 由于是读取前k个数，这里应该是UpAdd
  }


  // 遍历文件中剩余的数，维护最小堆
  int x = 0;
  while (fscanf(fout, "%d", &x) != EOF)
  {
    if (x > minheap[0]) // 只有新的数比堆顶大时，才替换并进行下沉
    {
      minheap[0] = x;
      DnAdd(minheap, 0, k); // 注意这里是对堆顶进行下沉，所以传入的应该是0
    }
  }


  // 输出结果
  HeapSort(minheap, k); // 排序最小堆，使之按照顺序输出
  for (int i = 0; i < k; i++)
  {
    printf("%d ", minheap[i]);
  }
  printf("\n");


  free(minheap); // 释放内存
  fclose(fout); // 关闭文件
}

---

结论

堆排序是一种非常有效的排序算法，特别适用于大数据集。通过利用堆的属性，它能够以 (O(n \log n)) 的时间复杂度进行排序。这篇文章通过C语言示例展示了堆排序的实现，希望能帮助你更好地理解这个强大的算法。