欢迎来到博主的专栏——C语言与数据结构
博主ID——代码小豪

如何判断代码的好坏

实现相同作用的不同代码，如何分辨这些代码的优劣之处呢？

有人说了，我写的代码10行，别人写的是20行，我的代码更加简洁。那就是好代码

在可读性方面可能会更优（简洁≠可读性高），但是一个软件的使用者是用户啊，用户不需要能够看明白你的代码，用户需要的是软件的使用体验。

因此判断一个算法的好与劣可以用运行时间来衡量。

那么如何得到一个程序的运行时间呢？最好的方法当然是运行测试一下。但是这样做的问题也就出现了。

我用一台00年的电脑，和一台24年电脑运行一段代码，当然是24年的电脑运行更快啦，甚至有可能是24年的电脑运行坏代码比00年的电脑运行好代码更快。那么难道能说运行快的代码比较好？

这种判断的方法明显受到了硬件层面的影响，程序员应该专注于程序，在程序方面来判断算法的优劣，于是时间复杂度和空间复杂的概念就出现了。

这两个概念是用来判断实现的代码的算法的优劣性的。

时间复杂度

代码的运行时间，和算法的执行次数是明显呈现正相关关系的。

比如那个写了10行的代码，但是循环了100多次。而那个写了20行的代码，只需要执行1次。那么很明显，后者的运行时间快于前者。

时间复杂度的判断也是基于此，通过计算算法的执行次数来估计程序的运行快慢

什么是时间复杂度

时间复杂度是一个数学函数，用来评估一个算法在n的输入规模下，与执行指令的次数的关系

以计算1~n的各个数之和为例。常见的算法有以下两种

int sum_of_nums(int n)
{
	int sum = 0;
	for (int i = 1; i < n; i++)
	{
		sum += i;
	}
	return sum;
}

可以发现，当n为100时，这个算法执行的指令次数为202次

```c
int sum_of_nums(int n)
{
	int sum = 0;//1次
	for (int i = 1; i <= n; i++)//100次
	{
		sum += i;//100次
	}
	return sum;//1次
}

如果输入为n，那么这个算法执行的指令总次数为2n+2次。

高中数学学过等差数列的求和公式为

Sn=n*(a1+an)/2

而1~n的整数求和本质上也就是a1为1，an为n的等差数列求和，所以用这种算法写出来的代码如下

int sum_of_nums(int n)
{
	int sum = 0;
	sum = n * (1 + n) / 2;
	return sum;
}

这个算法无论输入N等于多少，指令的执行次数都是3次。

很明显后者的算法优于前者，并且随着n的增加，后者的优势会更加明显。

那么我们假设还有一种算法，其实现是这样的

int sum_of_nums(int n)
{
	int sum = 0;
	for (int i = 1; i <= n; i++)
	{
		for (int j = 1; j <= i; j++)
		{
			if (j == i)
				sum += j;
		}
	}
	return sum;
}

如果输入为n，这个算法执行的次数为（1+2+3+……+n）+2，即n/2+n^2/2+2.

将上述算法的指令执行次数和输入规模的关系画成一个函数关系图，图形如下：

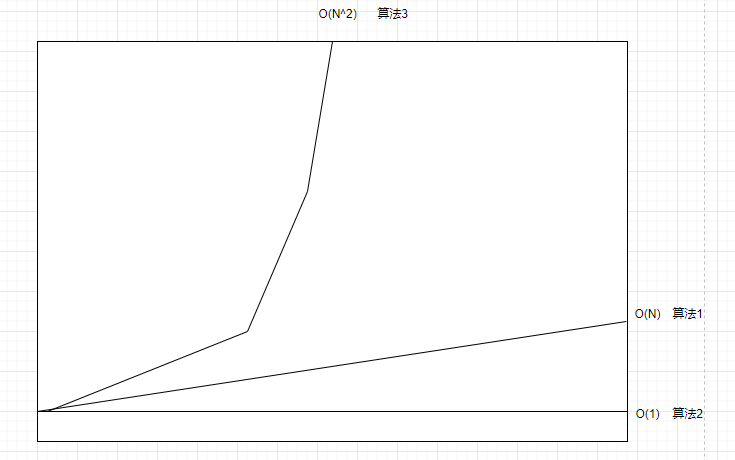
（手绘图形，不会画曲线–+）

根据图形，算法一：f(N)=2N+2是一个线性函数，因此时间复杂度是O（N），也就是常说的线性阶

算法2 f(N)=3,可以看到图像是一个常数函数，因此时间复杂度为O（1），也就是常数阶。

算法3 f(N)=N/2+N^2/2+2 可以看到图像是一个指数函数，因此时间复杂度为O（N^2）,即指数阶。

时间复杂度O（f（n））是用来评定算法的快慢的，大O阶实际上是一个估值。或者说是一个算法的评级，常见的复杂度有以下几种
（1）常数阶，O（1）
（2）线性阶，O（2）
（3）对数阶，O（logN） （二分查找就是典型的O（logN）的算法）
（4）指数阶，O（N^2）

看到这有人就觉得很疑惑了，比如我写的一个算法，运行指令和输入的关系函数f(n)=n,而别人的是f(n)=2n，但是为什么时间复杂度都是O（N）呢，明明我的程序更好啊，我不服。

实际上时间复杂度可以认为是一个算法的评级，比如考英语四级，我考了424，而别人考了100，虽然我的英语水平肯定高于100，但是英语的评级我们两个都是没过四级。

当然了，这种优化还是不错的，虽然没有将O（N）变成O（1），但是在运行速度当然会更快一步。

如何计算时间复杂度

时间复杂度的计算方式在上面就已经可以明显感觉到了。

即时间复杂度取决于输入与执行指令的关系函数的最高次数项。
比如f（N）=2N^2+22+3，那么这个算法的时间复杂度就是O（N^2）,实际上也是很好理解的，如下图

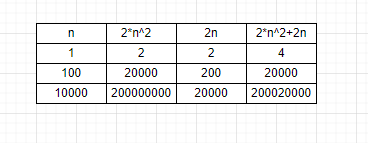
对比可以发现，当n超过一定数量的时候， 只有次数高的项对指令的运行次数影响最大，其余项可以忽略不计。

计算大O阶的方法总结
（1）只保留最高次数项
（2）保留的最高次数项将系数改为1
（3）如果只有常数项，那么就是1.

空间复杂度

算法中除了运行的指令外，还有用来存储数据的内存空间也是需要考虑在内的，但是现代的计算机对于空间的需求已经不再那么抠抠索索了，甚至大部分的算法采取的思路都是“以空间换取时间”。

比如判断1~10000的水仙花数，除了使用大量的指令让其计算以外，也可以创造一个10000元素大小的数组，将已知的水仙花数对应下标的元素记为1，这样子就从计算水仙花数的问题，变为了检索数组元素的问题，时间缩减，但是空间上要多出10000个元素的空间占用。

空间复杂度的计算公式为S（n）=O（f（n）），f（n）为执行指令时，对内存占用空间的函数，比如递归的空间复杂度就是O（n），因为每次执行递归，都会在内存中多开辟一个空间。