差分算法模板
- 一维差分
- 一维insert函数(构造差分数组和实现区域加数操作)
- 一维差分模板题
- 二维差分
- 二维insert函数(构造差分数组和实现区域加数操作)
- 二维差分模板题
一维差分
差分主要是计算出某个区域段的数分别加上一个数
先给定一个原数组a:a[1], a[2], a[3], a[n];
然后我们构造一个数组b : b[1] ,b[2] , b[3], b[i];
使得 a[i] = b[1] + b[2 ]+ b[3] +, + b[i]
也就是说,a数组是b数组的前缀和数组,反过来我们把b数组叫做a数组的差分数组。换句话说,每一个a[i]都是b数组中从头开始的一段区间和。
差分数组公式: b[i] = a[i] - a[i - 1]
一维insert函数(构造差分数组和实现区域加数操作)
我们先来讲讲用insert函数实现区域加数操作
我们要记得,a数组是b数组的前缀和数组,比如对b数组的b[i]的修改,会影响到a数组中从a[i]及往后的每一个数。
比如首先让差分b数组中的 b[l] + c ,a数组变成 a[l] + c ,a[l+1] + c, a[n] + c
理解了这一点,就可以推出以下的公式
b[l] + c,效果使得a数组中 a[l]及以后的数都加上了c(红色部分),但我们只要求l到r区间加上c, 因此还需要执行 b[r+1] - c,让a数组中a[r+1]及往后的区间再减去c(绿色部分),这样对于a[r] 以后区间的数相当于没有发生改变。
得出一维差分结论:给a数组中的[ l, r]区间中的每一个数都加上c,
只需对差分数组b做 b[l] + = c, b[r+1] - = c
同时,通过这个insert函数,我们也可以用来构造差分数组
void insert(int l, int r, int v)
{
b[l] += v;
b[r + 1] -=v;
}
for(int i = 1; i <= n; i++)
{
cin >> a[i];
insert(i, i, a[i]); //差分数组默认初始化为
}
根据差分数组公式:b[1] = a[1] b[2] = a[2] - a[1],
可以试着 模拟几次数据
i = 1时, 在[1, 1] 这个区间 加上a[i]—> b[1] = a[1] b[2] - = a[1]
i = 2时候, b[2] += a[2] --> 也就相当于 b[2] = a[2] - a[1]
(前面i = 1的时候,减去过a[1],后面i = 2时,加上a[2])
这种做法就比较巧妙
一维差分模板题

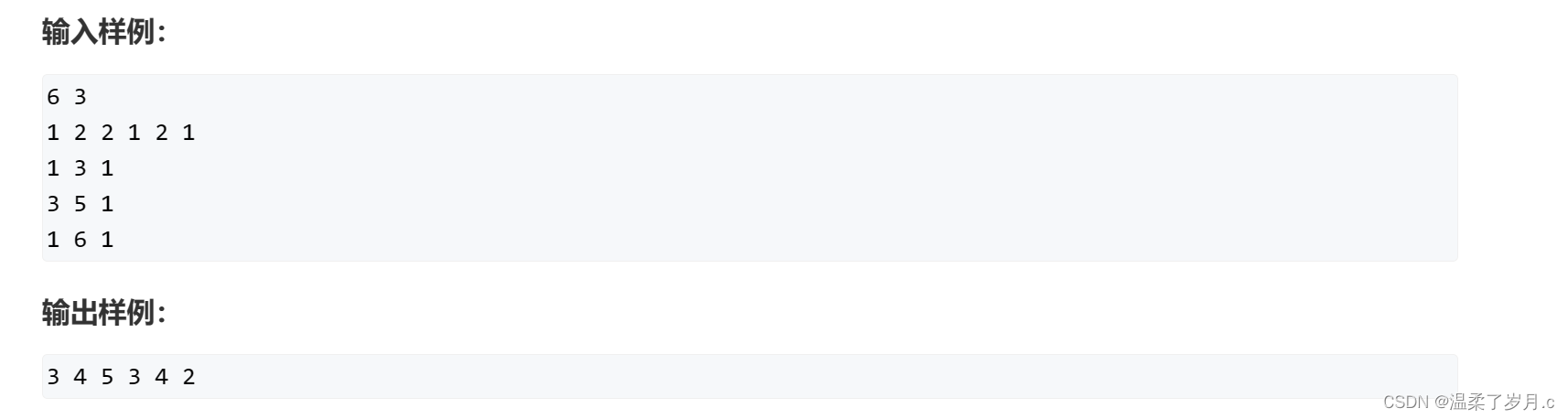
#include<iostream>
#include<cstdio>
using namespace std;
//一维差分模板
//差分的作用:就是用来计算某个区间断,加上某个数
//注意:差分和前缀和的数组下标都是从1开始的
const int N = 1e5 + 10;
int a[N]; //原数组
int b[N]; //差分数组
//差分数组的前缀和就是原数组
//差分数组的求法:
/*
差分数组默认初始化为0,但是要实现,在某个区间端加上某一个数
就要先有原来数组的数据,然后再进行加数的操作
这里统一,可以使用insert(int l, int r, int v)函数来进行操作
l代表左端点,r代表端点,v代表加的数的大小
函数的作用:在区间[l, r]这个区间中,加上v这个数
赋给原来数组的数据可以用 insert(i, i, a[i]);
例如 :b[1] = 0; 在i = 1的时候,在[1, 1]这个区间中插入 a[i]的值
但是由于插入之后,后面前缀和数组也要发生变化,所以后面也得减去v
b[l]变化 ,b[l]后面的也得变化,[l, r]也加上了v, 所以r + 1后面的,都减去v
*/
//注意:此处要假设 a[n] 是b[n]的前缀和
//即 : a[n] = b[1] + b[2] + b[3]...... + b[n];
void insert(int l, int r, int v)
{
b[l] += v;
b[r + 1] -=v;
}
int main()
{
int n, m;
cin >> n >> m;
for(int i = 1; i <= n; i++)
{
cin >> a[i];
insert(i, i, a[i]); //差分数组默认初始化为
}
int l, r, c;
while(m--)
{
cin >> l >> r >> c;
insert(l, r, c);
}
//算差分和数组
for(int i = 1; i <= n; i++)
{
b[i] += b[i - 1]; // 这里直接在原数组上进行了前缀和的计算,a[i] = b[i] + a[i - 1];
}
for(int i = 1; i <= n; i++)
{
> 这里是引用
cout << b[i] << " ";
}
return 0;
}
这里注意:算出差分数组b[i],并不是结果数组,结果数组是a[i],要对b[i]进行前缀和算出a数组
二维差分
一维变成二维,其他步骤基本没变化,变化的是insert函数
二维insert函数(构造差分数组和实现区域加数操作)
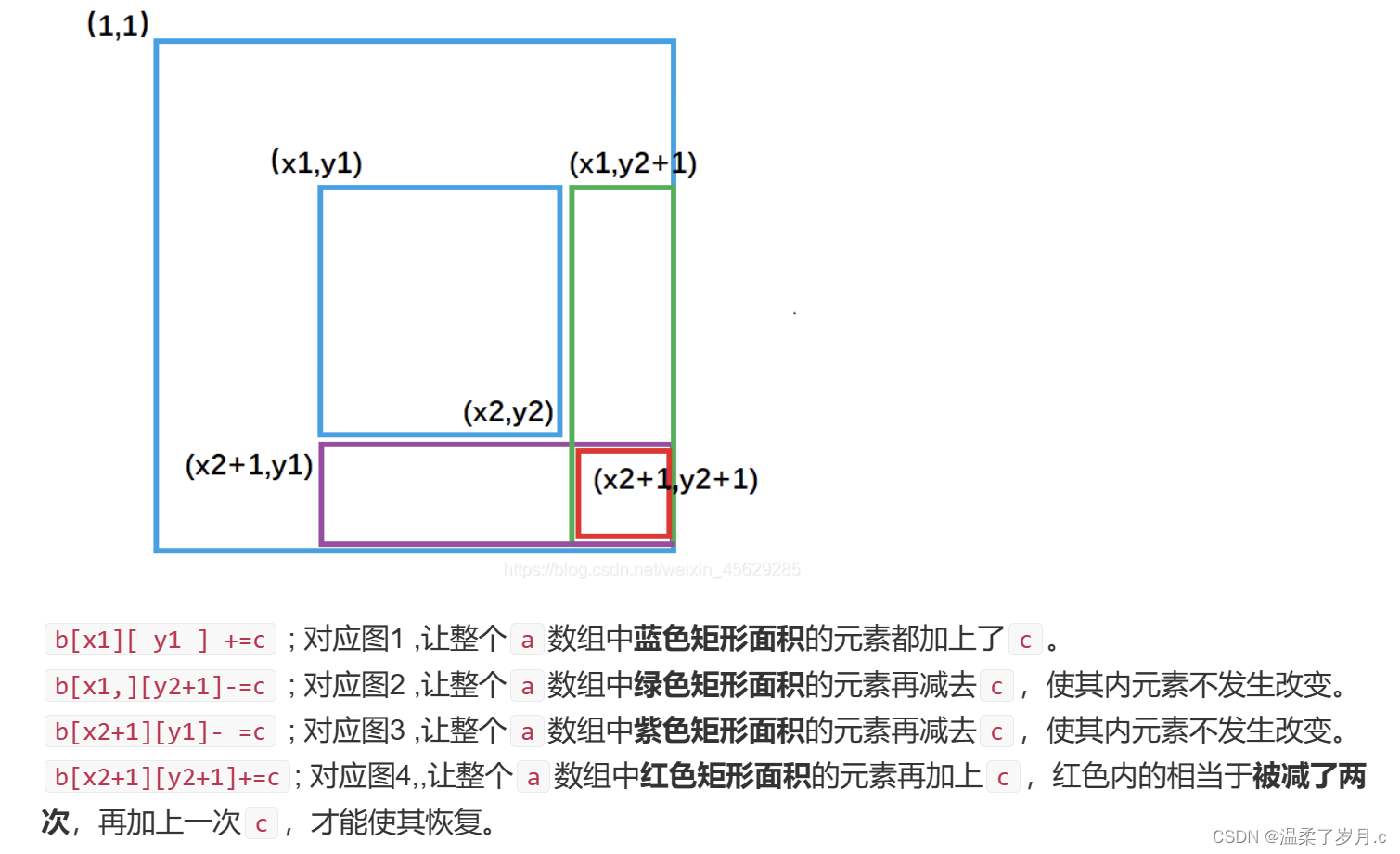
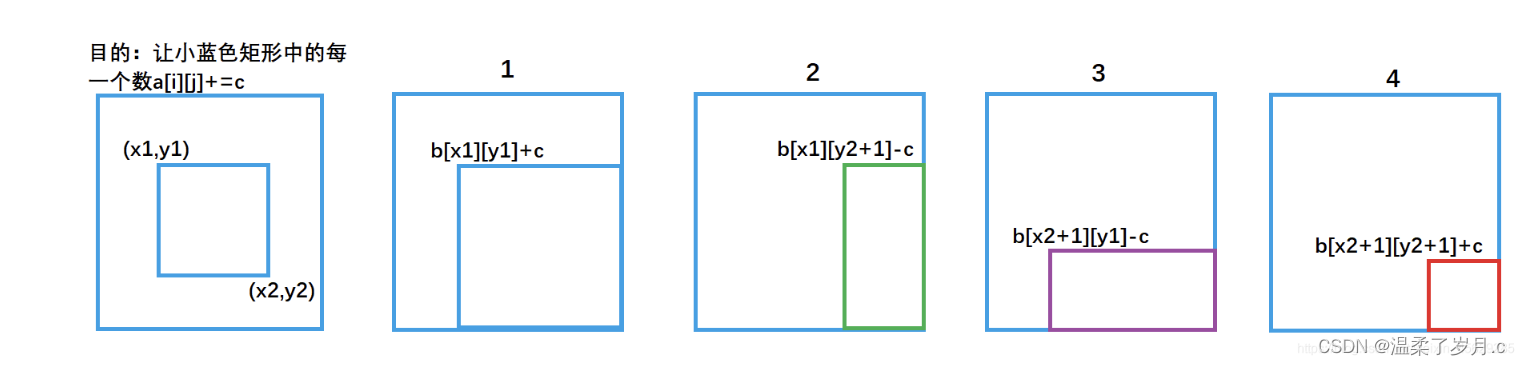
这里采用了acwing中一位大佬的题解,讲解的非常好
然后我们就得到了二维差分数组中的差分数组
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] += c;
b[x1][y2 + 1] -=c;
b[x2 + 1][y1] -= c
b[x2 + 1][y2 + 1] += c;
}
同样利用这个insert函数,也能构造出二维的差分数组,思路跟一维的类似,这里就不在详细说了,不懂的再去看看前面一维那部分的讲解。
二维差分模板题

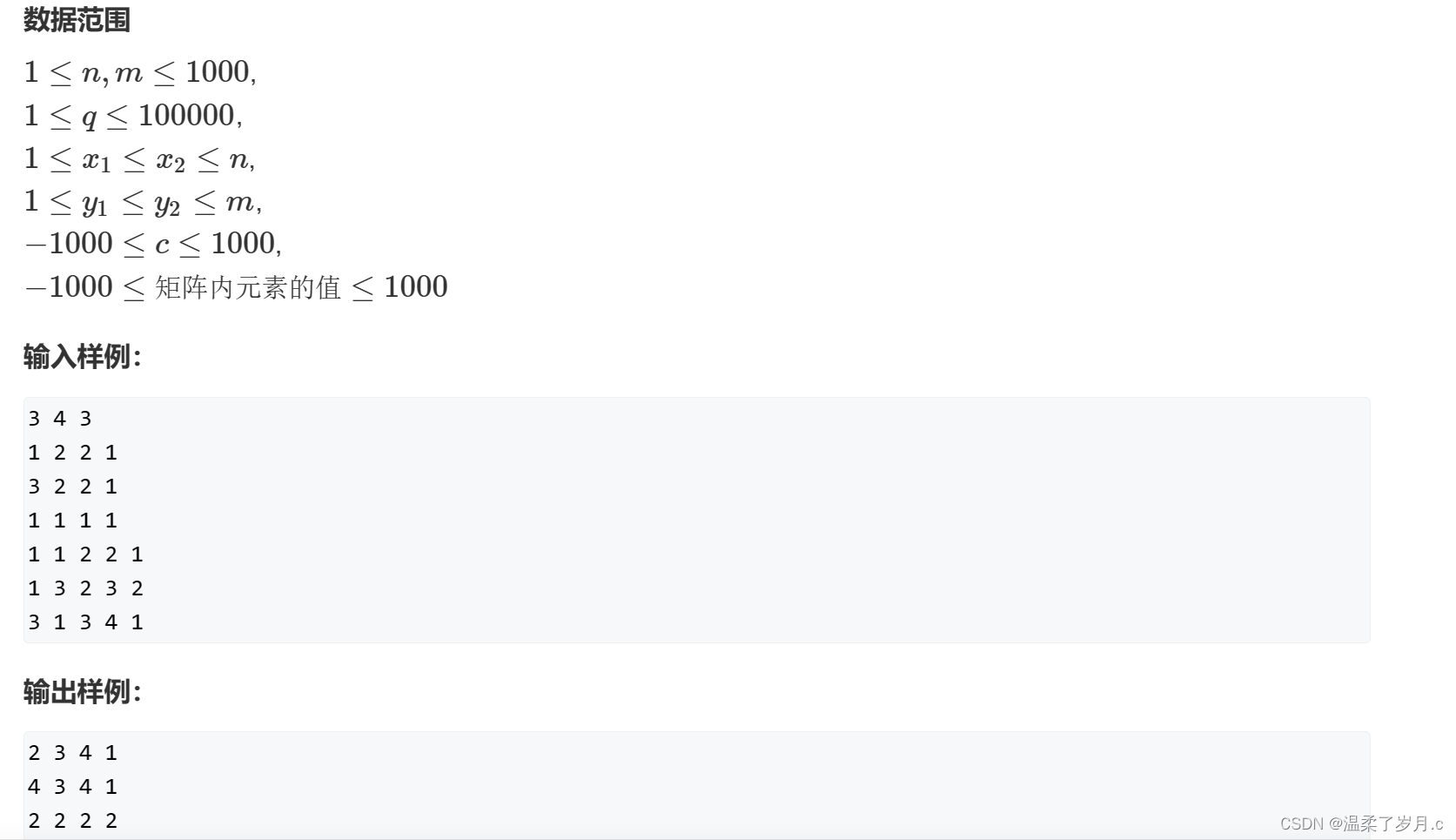
#include<iostream>
#include<cstdio>
using namespace std;
const int N = 1010;
int a[N][N],b[N][N];
int n, m, q;
void insert(int x1, int y1, int x2, int y2, int c)
{
b[x1][y1] +=c;
b[x2 + 1][y1] -=c;
b[x1][y2 + 1] -=c;
b[x2 + 1][y2 + 1] +=c;
}
int main()
{
cin >> n >> m >> q;
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
cin >> a[i][j];
insert(i, j, i, j, a[i][j]); //差分数组初始化
}
}
//区间加上某个数
int x1, y1, x2, y2, c;
while(q--)
{
cin >> x1 >> y1 >> x2 >> y2 >> c;
insert(x1, y1, x2, y2, c);
}
//算出a[n]
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
//可以在在b数组本身上进行前缀和加的计算()
//方式一:
//b[i][j] += b[i - 1][j] + b[i][j - 1] - b[i - 1][j - 1];
//也可以这样
//方式二:用原数组进行 a[i][j] = a[i -1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j]
a[i][j] = a[i - 1][j] + a[i][j - 1] - a[i - 1][j - 1] + b[i][j];
}
}
for(int i = 1; i <= n; i++)
{
for(int j = 1; j <= m; j++)
{
//方式一:
//cout << b[i][j] << " ";
//方式二:
cout << a[i][j] << " ";
}
cout << endl;
}
return 0;
}






![[NAND Flash 6.2] NAND 初始化常用命令:复位 (Reset) 和 Read ID 和 Read UID 操作和代码实现](https://img-blog.csdnimg.cn/direct/8da52f8b77e44747bd12bf0a356d75bc.png)