一、关系数据模型

1、关系数据结构

(1) 域、笛卡尔积、关系

笛卡尔积实际上可以看成是n个行向量，即（域），所组成的一个乘法算式，每一个行向量是一个Di，所有行向量逻辑上组合在一起就是D，就是一整个组域。其中呢，每一个行向量表示同一类的数据，例如

D1=班级集合，class = {计算机1班、计算机2班....}、

其中“计算机1班”这样的，叫分量，整个class叫做元组。

那么，笛卡尔积怎么乘呢？

再给一个D2=学生，student={张三，李四}

D1XD2=(计算机1班，张三)，（计算机1班，李四），（计算机2班，张三），（计算机二班，李四）

说白了，假如D1={a1,a2,a3...an}，D2={b1,b2,b3,b4....bn}，D1XD2=a1*b1+a1*b2+..a1*bn+a2*b1+a2*b2.....an*b1+an*b2...an*bn。酱紫

其实有是高数里面的叉乘，只不过元素从数字换成字符。

至于关系，

D1XD2XD3....XDn，这个笛卡尔积的子集就是在这一组域里的关系，一般表示成R(D1,D2,D3....Dn).

2、基本术语

这玩意儿乱七八糟一大堆的，建议找几个表格对着了解一下，这里不再赘述。

但有个地方要注意到，那些个候选码（其中几个比较重要的列），主键（人为挑选的一个候选码，有且只有一个），主属性（任意候选码中的一个元素，即aij）,非主属性，外键。

二、关系的完整性

三类完整性：实体完整性规则（主键属性不为空）、参照完整性规则（）、用户定义完整性规则。

三、关系代数

1、 传统集合运算

并、差、交、笛卡尔积，这就不说了，大家都懂

2、专门的关系运算

这里要记住相关的符号，因为后面的知识点很多，这里的记忆很容易模糊就留下个印象，但是印象不是真的记住了，要有清晰的认知。

选择、投影、连接、除运算，书上自己看去，东西贼多，我自己还要复习呢

注意点：

（1）选择书写时，注意下标是否带有引号，有引号的话就是比较固定的字符，没有的话，就是对应的行每个分量都要比较。

（2）投影的下标是选择哪些列组成新的关系。

（3）连接的关系是R的列和S的列的比较而不是RXS的新表的比较

（4）自然连接是一种比较特殊的，连接的R和S都有共同属性，而且每种共同情况只出现一次。

（5）除，实质上就是找出R中，非共同属性对应的共同属性的值中，包含S共同属性的所有值的种类，好复杂，你可能看不懂，但是你看完书上的例子之后，就会理解我的意思，要一边看一边想，脑里要浮现一个类似的表，顺着想几次就明白了。

（6）实例中，若是牵扯到好几个表，就在最里层把几个表连接或者笛卡尔积，然后再通过选择和投影筛选目标，而且这几个表一定有共同属性。那么问题来了，什么时候用笛卡尔积？什么时候用连接呢？我从书上看到一个很诡异的地方，如下图

简直怀疑我的眼睛，我看到了累乘符号，给我整懵了，赶紧上网搜一下。

首先是，什么时候用的问题。

当没有共同属性时，自然连接就变成笛卡尔积，但是这里应该是指那种“自己X自己”的情。，就是检索自己表中的多个条件同时成立时，计算机会把一个表复制多份，然后当成多个不同的表比较，所以这里就需要自然连接；又因为自己X自己不存在共同属性的说法，所以就用了笛卡尔积。

数据库--关系代数复杂操作（除、外连接）带关系代数应用训练_复杂关系代数实例-CSDN博客

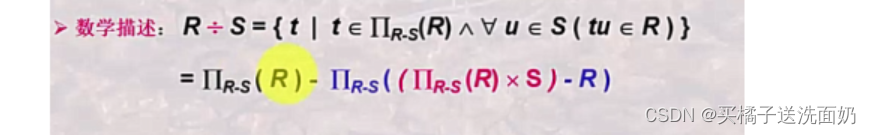
我在这里发现了盲点....个屁的，这里是打印问题，其实这个符号是π，千万不要被误导了！！

上面也是，上面的也不是累乘符号∏，而是π...书本误我！

3、关系代数的扩充操作

这里可能大家都比较陌生，老师上课应该都会说不是本科重点内容，所以就大致提一下。

外连接、改名、广义投影、赋值、外部并、聚集操作

但其实也比较好理解，自己看看就行。同样的，也需要注意一下表达式的格式，可以自己写写画画，增加印象。

注意点：

（1）改名的时候，可能会使非共同属性，变成共同属性，这就导致符号从笛卡尔积变成连接。

（2）外连接和外部并不要搞混了，外连接是先自然连接，再补上对应边没有‘对象’的那一行，并发个null做‘对象’；外部并，其实可以看成，把两个表的所有项都保留，然后在空的地方用null填充。

（3）聚集操作不再局限于表中的关系，还牵扯到对应值得计算，具体公式，看题目要求。

四、关系演算

1、元组关系演算

这里的各种公式和高等数学的各种关系。公式很像，只不过一个是列表元组，一个是集合元素，可以对比学习。

而且这里的元组变量好像都是从1开始的，而不是从0，这里要区别开来

其中还有一些等价的转换规则，第一个类似德摩根律，就是

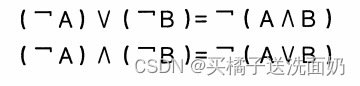
很经典，剩下俩我看的也有点懵，最好的理解方式，就是自己写两个关系表，然后跟着试一下，看看建立的新表两边是不是一样

（我估计这里，会懒得慢慢看直接就跳过去了，没错，我也是(〃'▽'〃)）

哦对了，前面的关系代数表达式可以转化成这里的关系表达式，书上一堆例题，可以自己跟着练习一下。

注：我查了一下网上好像没有什么具体解释笛卡尔积从关系代数表达式到关系表达式的过程，这玩意儿还巨长，我就决定自己摸索一下，下面是思路：

首先，经过观察，发现等式最右边都是以t结尾，并且从1到6，这里R和S可以看成两个三元组的关系即都是有三行，列不影响。通过前面可知，笛卡尔积其实是前面每一个和后面每一个对应组成新元组的过程。这里的t是满足整个公式的所有元组的集合。

额，咋说呢，这里不像上面的表示RUS和R-S的元组表达式，他没有吧具体的过程表示出来，他只是表示一种正确关系，比如第一部分，表示R和S共有的部分会在RXS的第一行出现，R的第一行会在RXS的第二行出现，这样子，就比较...毕竟咱也不是数学家，就当练练脑子了(￣ェ￣;)。

等等，好像不太对劲。

好像应该是这样才对，好乱...这里就先这样，回头二轮的时候再出一期，到时候再搞清楚，上面的都是◐◆☹☹☺☽☚♂♦☞㏂㏘，不要进脑子里！

2、域关系演算

这里限制的是值域，通常用xyz之类的表示某一列，然后这里挑选的是列中数值在值域范围中的，条件全满足的元组，挑出来组成新的关系。

3、关系演算的安全约束和等价性

防止无限关系和无穷验证的出现，比如，关系演算中有“非”，这种符号的存在，就会导致无限的存在。

所以，要给个DOM就是给定一个固定的值域，然后反过来限制定义域，使得取得的值经过演算之后的结果在值域内。

大致就是酱紫