题目链接
本题是2002年ICPC亚洲区域赛金沢(日本)赛区的H题
题意
我已经把n个圆盘依次放到了桌面上。现按照放置顺序依次给出各个圆盘的圆心位置和半径,问最后有多少圆盘可见?如下图所示。

分析
《训练指南》的题解:
题目说“保证在对输入数据进行微小扰动后答案不变”,意味着圆盘的可见部分不会太小。不难发现,每个可见部分都是由一些“小圆弧”围成的,因此可以先求出所有小圆弧,然后判断每段小圆弧是否可见(在程序实现中,可以用圆弧中点代替整条圆弧进行判断)。小圆弧可见,意味着它所在的圆是可见的。接下来,对于所有可见的小圆弧,看看这段圆弧中点的正下方都有哪些圆盘,则其中最顶部的圆盘也是可见的(想一想,为什么)。
如何求出所有小圆弧?所有圆两两求交点,则每个圆上任两个相邻交点之间的圆弧就是所求。需要注意的是,如果一个圆不和其他所有圆相交,则整个圆是一条所求圆弧。
这个思路真的很巧,特此写一篇笔记加强印象,还有一些细节参见AC代码。
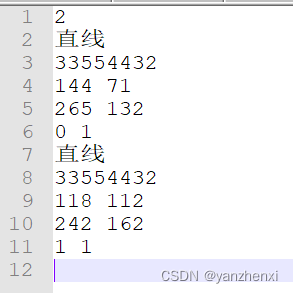
这里给一份测试数据,以及我用python写的画图可视化分析数据的脚本,能方便看出每个圆被其上面有相交的那些圆的覆盖情况:


AC代码
#include <iostream>
#include <cmath>
#include <algorithm>
using namespace std;
#define N 102
double a[N][N<<1], x[N], y[N], r[N], z = M_PI + M_PI; bool vis[N], esc[N]; int c[N], n;
double check(double x) {
return x > M_PI ? x-z : (x < -M_PI ? x+z : x);
}
void judge(int i, double a) {
double px = x[i] + r[i]*cos(a), py = y[i] + r[i]*sin(a);
for (int j=i+1; j<n; ++j) if (sqrt((px-x[j])*(px-x[j])+(py-y[j])*(py-y[j])) < r[j]) return;
vis[i] = 1;
for (int j=i-1; j>=0; --j) if (sqrt((px-x[j])*(px-x[j])+(py-y[j])*(py-y[j])) < r[j]) {
vis[j] = 1; return;
}
}
void solve() {
for (int i=0; i<n; ++i) cin >> x[i] >> y[i] >> r[i], c[i] = vis[i] = esc[i] = 0;
for (int i=0; i<n; ++i) for (int j=i+1; j<n; ++j) {
double dx = x[i]-x[j], dy = y[i]-y[j], d = sqrt(dx*dx + dy*dy);
if (d <= max(r[i], r[j])-min(r[i], r[j])) {
if (r[i] <= r[j]) esc[i] = 1;
continue;
}
if (d < r[i]+r[j]) {
double x = atan2(dy, dx), b = acos((d*d+r[j]*r[j]-r[i]*r[i])/d/r[j]/2),
y = M_PI - acos((d*d+r[i]*r[i]-r[j]*r[j])/d/r[i]/2);
a[j][c[j]++] = check(x+b); a[j][c[j]++] = check(x-b);
a[i][c[i]++] = check(x+y); a[i][c[i]++] = check(x-y);
}
}
for (int i=0; i<n; ++i) {
if (esc[i]) continue;
if (c[i]) {
sort(a[i], a[i]+c[i]);
judge(i, (a[i][c[i]-1] + a[i][0]) / 2 + M_PI);
for (int j=c[i]-1; j>0; --j) judge(i, (a[i][j-1] + a[i][j]) / 2);
} else vis[i] = 1;
}
int ans = 0;
for (int i=0; i<n; ++i) if (vis[i]) ++ans;
cout << ans << endl;
}
int main() {
while (cin >> n && n) solve();
return 0;
}