题目链接:leetcode环形子数组的最大和
目录
题目解析:
算法原理
1.状态表示
2.状态转移方程
3.初始化
4.填表顺序
5.返回值
编写代码
题目解析:

题目让我们求返回 nums 的非空 子数组 的最大可能和
这道题如果是按照-这道题-是不对的,因为这道题中是环形数组。
这道题我们可以分情况讨论:
1.先按照之前的方法:子数组系列_最大子数组和
求出如果不是环形数组那么他的最大和是多少;
(求最大和)
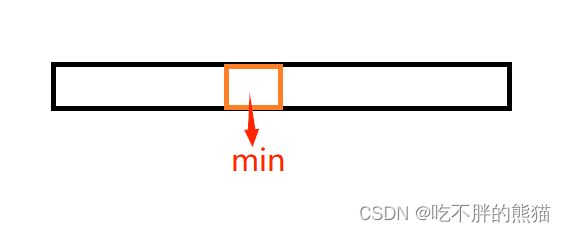
2.我们反过来想,这里题目求和最大值,
如果我们求得这个数组里的连续最小和,再用数组总和-最小和---》就可以得到这个数组的最大和
(求最小和)
算法原理:
1.状态表示
先创建一个dp表
首先先思考dp表里面的值所表示的含义(是什么?)
根据上面的分析,我们需要求两中状态的最大和:
f[i] 表示:以i 为结尾的所有子数组中的最大和
g[i] 表示:以i为结尾的所有子数组中的最小和
这种状态表示怎么来的?
1.经验+题目要求
用之前或者之后的状态,推导出dp[i][j]的值;
根据最近的最近的一步,来划分问题
2.状态转移方程
dp[i]等于什么?
一、(求最大值f[i]):
这里我们分两种情况讨论:
情况一:当连续子数组的长度==1
那么此时f[i]就应该等于该位置的值,即num[i];
所以得:f[i]=num[i];
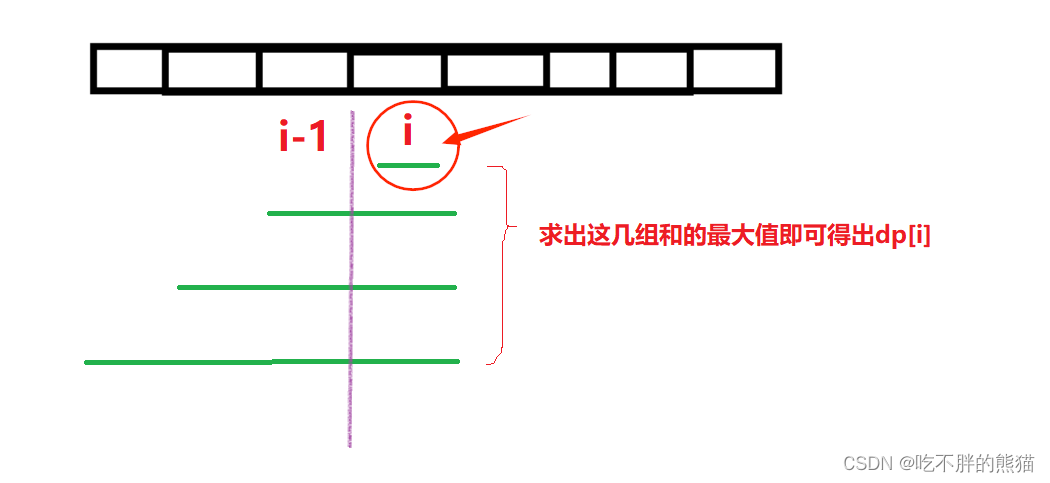
情况一:当连续子数组的长度>1
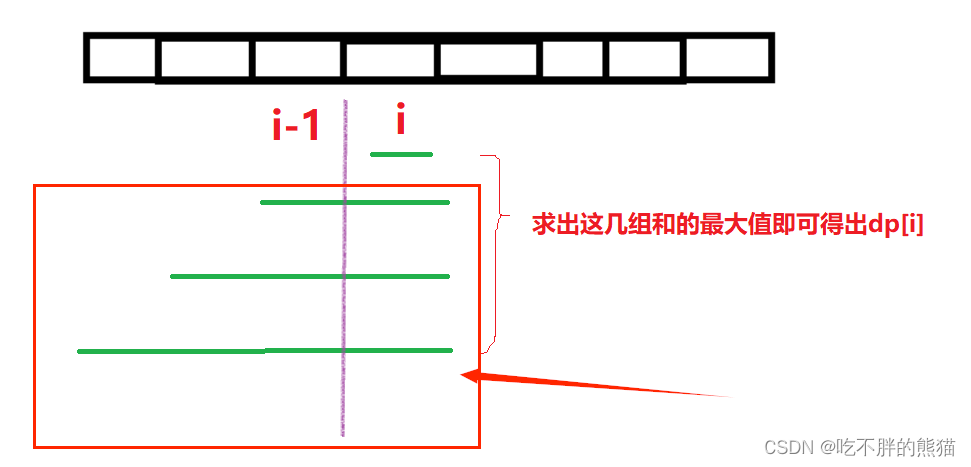
此时我们应该用i-1位置的最大和再加上i位置的值(num[i]),
而“i-1位置的最大和”就是f[i-1]
所以得f[i]=f[i-1]+num[i]
综上:
题目需要最大值,所以要取这两者的最大值:
即:f[i]=max(num[i],f[i-1]+num[i])
一、(求最小值g[i]):
同理g[i]=min(num[i],g[i-1]+num[i])
3.初始化
(保证填表的时候不越界)
根据状态转移方程,我们需要初始化[i-1]
这里我们采用创建虚拟节点的方式:
为了不让f[0]影响后续的值,
所以f[0]=g[0]=0;
4.填表顺序
(为了填写当前状态的时候,所需要的状态已经计算过了)
这里所需要的状态是:
这里所需要的状态是:i-1
所以从左到右
5.返回值
(根据题目要求和状态表示)
综上分析:
如果最小值==数组和,说明该数组中都是负数,
此时只需返回f表里的最大值就可以了
否则就返回数组和-g表里的最小值就可以得到最大值
编写代码:

class Solution {
public:
int maxSubarraySumCircular(vector<int>& nums) {
//1.创建dp表
//2.初始化
//3.填表
//4.返回结果
int n=nums.size();
vector<int> f(n+1);
auto g=f;
int rmax=INT_MIN;
int rmin=INT_MAX;
int sum=0;
for(int i=1;i<n+1;i++)
{
int x=nums[i-1];
f[i]=max(x,f[i-1]+x);
rmax=max(f[i],rmax);
g[i]=min(x,g[i-1]+x);
rmin=min(g[i],rmin);
sum+=nums[i-1];
}
return sum == rmin ? rmax : max(rmax, sum - rmin);
}
};