什么是机器学习
支持向量回归(Support Vector Regression,SVR)是一种基于支持向量机(Support Vector Machine,SVM)的回归算法,用于解决回归问题。与传统的回归算法不同,SVR的目标是通过构建一个预测函数,使得预测值与实际值的差异最小化。
SVR 在解决回归问题时的主要思想是通过寻找一个决策边界,使得预测值与实际值之间的差异尽可能小,并且在一定的容忍度内。支持向量回归有几个关键的概念:
- 支持向量: 在 SVR 中,数据点被表示为特征空间中的点,而那些对构建决策边界有重要影响的数据点称为支持向量。这些支持向量是用来确定决策边界的关键点。
- 间隔(Margin): 与分类问题中的 SVM 类似,SVR 也有间隔的概念。在 SVR 中,间隔是指在决策边界周围的一条带,其中的数据点对模型的影响较小。SVR 的目标是找到一个最大化间隔的决策边界,同时允许一些数据点落在间隔之内。
- 损失函数: SVR 使用一个损失函数来度量预测值与实际值之间的差异。典型的损失函数是
epsilon-insensitive损失函数,它允许在一定的容忍度(epsilon)内不计算损失。
SVR 的核心思想是通过优化问题来找到一个最佳的超平面,使得模型的预测误差最小。具体来说,SVR 的优化问题可以表示为:
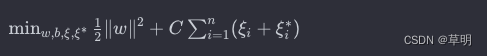
其中 :
w是权重向量b是偏置C是正则化参数ξi和ξi^*是松弛变量,用于处理间隔内的误差
这个问题的解决方法通常使用拉格朗日乘数法和 KKT 条件。
在实际应用中,你可以使用机器学习库中的 SVR 实现,比如 Scikit-Learn。以下是一个简单的 Scikit-Learn SVR 的使用示例:
from sklearn.svm import SVR
import numpy as np
import matplotlib.pyplot as plt
# 创建示例数据集
np.random.seed(42)
X = 5 * np.random.rand(100, 1)
y = np.sin(X).ravel() + 0.1 * np.random.randn(100)
# 创建 SVR 模型
svr = SVR(kernel='rbf', C=100, gamma=0.1, epsilon=0.1)
# 在训练集上训练模型
svr.fit(X, y)
# 生成预测结果
X_test = np.linspace(0, 5, 100).reshape(-1, 1)
y_pred = svr.predict(X_test)
# 可视化结果
plt.scatter(X, y, color='darkorange', label='data')
plt.plot(X_test, y_pred, color='navy', lw=2, label='SVR')
plt.xlabel('data')
plt.ylabel('target')
plt.title('Support Vector Regression')
plt.legend()
plt.show()
在上述示例中,SVR 类的 kernel 参数指定了核函数的类型(这里使用了径向基函数核,即 'rbf'),C 是正则化参数,gamma 是核函数的系数,epsilon 是 epsilon-insensitive 损失函数的容忍度。在实际应用中,你可能需要根据你的数据和问题来调整这些参数。