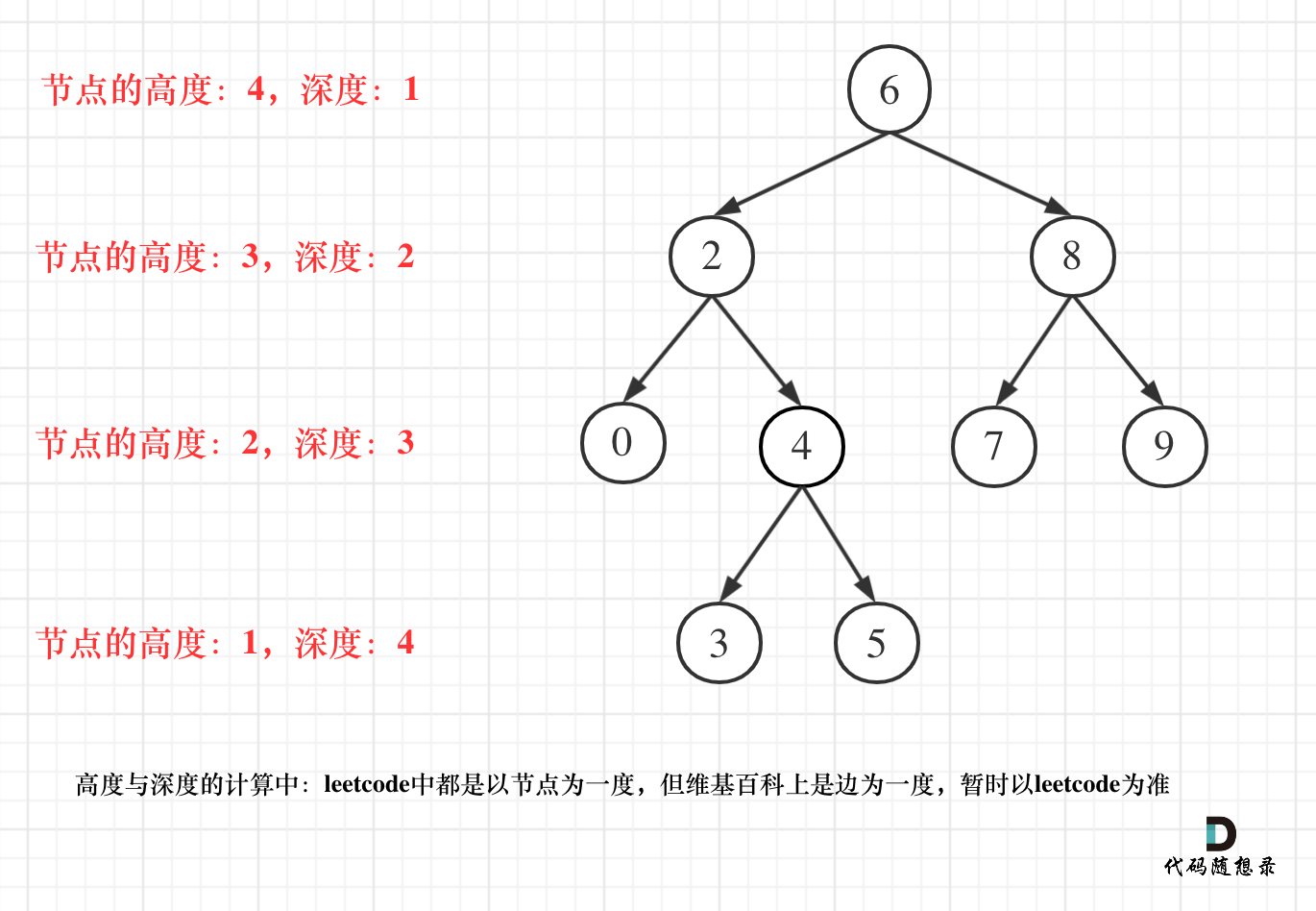
函数的形参列表
int func(int v,int v2)
{
int v,v2;//!错误
}函数返回类型
不能是数组和函数(两者都不接受对拷),但可以是指针
局部对象
形参和函数体内部的变量称为局部变量,仅在函数内部可见,隐藏外部变量
自动对象:只存在于块执行期间的对象
形参是自动对象
未初始化的自动对象赋未定义的值(随机数)
局部静态对象:在函数体内用static
size_t count_calls()
{
static size_t ctr=0;
return ++ctr;
}
ctr只被初始化一次,若不写初始化也是0
其与全局变量放在一个区域函数声明
也叫函数原型,把函数体去掉加分号 可省略形参名字
函数可声明多次,只可定义一次
最好在头文件声明
分离式变异
可以有.h .cpp .cpp三个文件一起编译
练习题
目前无需要强调的练习题







![XCTF:CatCatCat[WriteUP]](https://img-blog.csdnimg.cn/direct/1459637b37354e78abb4bd0ce1266f7e.png)