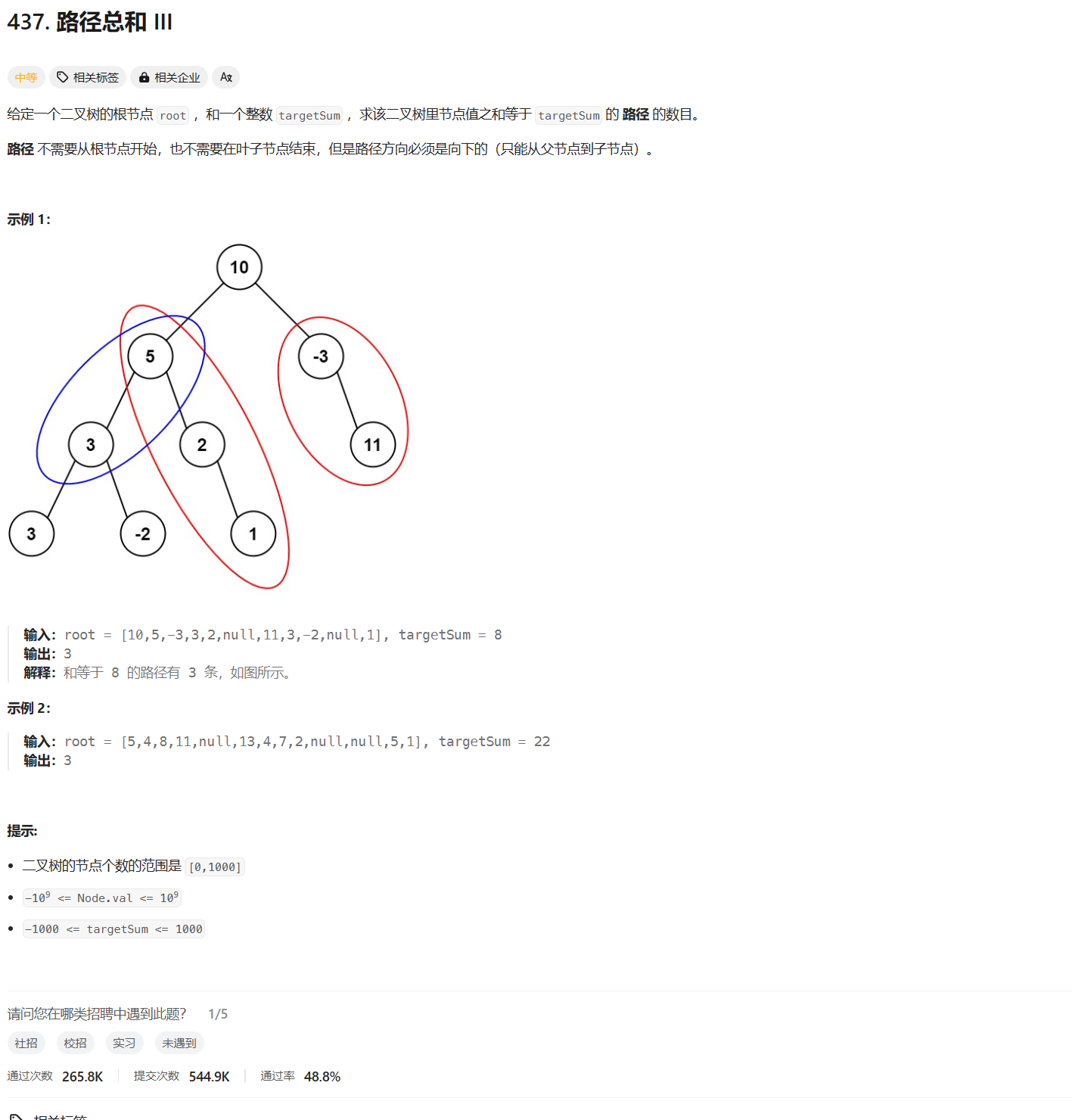
Problem: 437. 路径总和 III

思路

树的遍历 + DFS
一个朴素的做法是搜索以每个节点为根的（往下的）所有路径，并对路径总和为 targetSumtargetSumtargetSum 的路径进行累加统计。

使用 dfs1 来搜索所有节点，复杂度为 O(n)O(n)O(n)；在 dfs1 中对于每个当前节点，使用 dfs2 搜索以其为根的所有（往下的）路径，同时累加路径总和为 targetSumtargetSumtargetSum 的所有路径，复杂度为 O(n)O(n)O(n)。

👨‍🏫 参考题解

💖 树的遍历 + dfs

时间复杂度, 示例： $O(n^2)$

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
	long ans, t;// ans 统计符合要求的路径数量，t 记录目标值

	public int pathSum(TreeNode root, int targetSum)
	{
		t = targetSum;
		dfs1(root);
		return (int) ans;

	}

//	遍历 root 的所有子结点
	private void dfs1(TreeNode root)
	{
		if (root == null)
			return;
		dfs2(root, root.val);
		dfs1(root.left);
		dfs1(root.right);
	}

//	以 root 为根遍历其所有合法路径
	private void dfs2(TreeNode root, long val)
	{
		if (val == t)// 如果当前路径和恰好 == 目标值 ans++
			ans++;
		if (root.left != null)// 向左子树延申路径
			dfs2(root.left, val + root.left.val);
		if (root.right != null)// 向右子树延申路径
			dfs2(root.right, val + root.right.val);
	}
}

💖 树的遍历 + 前缀和

👨‍🏫 参考题解

时间复杂度, 示例： $O(n)$
从根节点到每个叶子结点的路径唯一，这就是一个前缀和

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
	long ans, t;// ans 统计符合要求的路径数量，t 记录目标值

//	注意：map集合只会包含当前结点的 祖先结点 的前缀和（在递归的过程种进行恢复现场）
	Map<Long, Integer> map = new HashMap<>();// key是前缀和，value是前缀和为key的结点数量

	public int pathSum(TreeNode root, int target)
	{
		if (root == null)
			return 0;
		t = target;
		map.put(0L, 1);
		dfs(root, root.val);
		return (int) ans;
	}

	/**
	 * @param root 当前根节点
	 * @param val  以当前root为尾结点的前缀和（此值唯一）
	 */
	private void dfs(TreeNode root, long val)
	{
		// 当前点前缀和(val) - 前边点的前缀和(map的key) == t
		// key = val - t，此 key 存在，证明前缀和可以实现
		if (map.containsKey(val - t))
			ans += map.get(val - t);
		map.put(val, map.getOrDefault(val, 0) + 1);//把当前点的前缀和作为 key 存进 map中
//		递归遍历当前树的左右子树
		if (root.left != null)
			dfs(root.left, val + root.left.val);
		if (root.right != null)
			dfs(root.right, val + root.right.val);
//		把当前点的前缀和作为 key 从 map 中取出，因为上边两个递归已经把它的子树（后代节点）都处理完了（留着也没用）
//		恢复现场：当前分支产生的影响不应该干扰到当前结点的兄弟分支的结果
		map.put(val, map.getOrDefault(val, 0) - 1);
	}
}