Planning模块,路径和速度曲线抽象成折线(Polyline),障碍物抽象成多边形(Polygon)。在碰撞检测、投影计算距离、平滑曲线等方面应用广泛。
1 几何算法
1.1 线段
moudles/common/math/line_segment2d.h
namespace apollo {
namespace common {
namespace math {
// 平面线段
class LineSegment2d {
public:
LineSegment2d();
LineSegment2d(const Vec2d &start, const Vec2d &end);
// 获取线段的起点
const Vec2d &start() const { return start_; }
// 获取线段的终点
const Vec2d &end() const { return end_; }
// 获取从起点到终点的方向
const Vec2d &unit_direction() const { return unit_direction_; }
// 获取线段的中心
Vec2d center() const { return (start_ + end_) / 2.0; }
// 旋转线段的终点
Vec2d rotate(const double angle);
// 返回线段的航向
double heading() const { return heading_; }
// cos(heading_)
double cos_heading() const { return unit_direction_.x(); }
// sin(heading_)
double sin_heading() const { return unit_direction_.y(); }
// 获取线段的长度
double length() const;
// 获取线段长度的平方
double length_sqr() const;
/**
* @brief Compute the shortest distance from a point on the line segment
* to a point in 2-D.
* @param point The point to compute the distance to.
* @return The shortest distance from points on the line segment to point.
*/
// 计算线段上的点到2-D中的点的最短距离。
double DistanceTo(const Vec2d &point) const;
/**
* @brief 计算线段上一点到二维中一点的最短距离,得到线段上最近的点
* @param point The point to compute the distance to.
* @param nearest_pt The nearest point on the line segment
* to the input point.
* @return 线段上的点到输入点的最短距离
*/
double DistanceTo(const Vec2d &point, Vec2d *const nearest_pt) const;
// 计算线段上的一点到2-D中的一点的最短距离的平方
double DistanceSquareTo(const Vec2d &point) const;
// 计算二维中线段上一点到一点的最短距离的平方,得到线段上最近的点。
double DistanceSquareTo(const Vec2d &point, Vec2d *const nearest_pt) const;
/**
* @brief 检查一个点是否在线段内
* @param point 检查它是否在线段内的点
* @return 输入点是否在线段内
*/
bool IsPointIn(const Vec2d &point) const;
// 检查该线段是否与二维中的另一条线段相交
bool HasIntersect(const LineSegment2d &other_segment) const;
// 计算与二维中另一条线段的交点(如果有的话)
bool GetIntersect(const LineSegment2d &other_segment,
Vec2d *const point) const;
// 计算矢量在线段上的投影
double ProjectOntoUnit(const Vec2d &point) const;
// 计算向量与线段的叉积
double ProductOntoUnit(const Vec2d &point) const;
// 计算从线段展开的直线上的二维点的垂直脚部
double GetPerpendicularFoot(const Vec2d &point,
Vec2d *const foot_point) const;
// 获取包含基本信息的调试字符串
std::string DebugString() const;
private:
Vec2d start_;
Vec2d end_;
Vec2d unit_direction_;
double heading_ = 0.0;
double length_ = 0.0;
};
} // namespace math
} // namespace common
} // namespace apollo
moudles/common/math/line_segment2d.cc
计算点到直线的距离
double LineSegment2d::DistanceTo(const Vec2d &point) const {
// 如果线段的长度小于等于一个阈值kMathEpsilon,那么点一定在线段上,直接返回点与线段起点的距离
if (length_ <= kMathEpsilon) {
return point.DistanceTo(start_);
}
const double x0 = point.x() - start_.x();
const double y0 = point.y() - start_.y();
// proj,表示点在方向向量上的投影
const double proj = x0 * unit_direction_.x() + y0 * unit_direction_.y();
// 如果投影小于等于0,说明点在直线段的同侧,直接返回点到线段起点的距离
if (proj <= 0.0) {
return hypot(x0, y0);
}
// 如果投影大于等于线段长度,说明点在直线段的延长线上,直接返回点到线段终点的距离
if (proj >= length_) {
return point.DistanceTo(end_);
}
return std::abs(x0 * unit_direction_.y() - y0 * unit_direction_.x());
}
给定一个点,计算到线段的最短距离,同时返回最近的点(过给定点的垂线与原线段的交点,或者线段的端点)
double LineSegment2d::DistanceTo(const Vec2d &point,
Vec2d *const nearest_pt) const {
// 检查nearest_pt是否为空
CHECK_NOTNULL(nearest_pt);
// 如果线段的长度小于等于一个阈值kMathEpsilon,那么点一定在线段上,直接返回点与线段起点的距离
if (length_ <= kMathEpsilon) {
*nearest_pt = start_;
return point.DistanceTo(start_);
}
// 计算点与线段起点的坐标差x0和y0
const double x0 = point.x() - start_.x();
const double y0 = point.y() - start_.y();
// 计算proj,表示点在方向向量上的投影
const double proj = x0 * unit_direction_.x() + y0 * unit_direction_.y();
// 如果投影小于等于0,说明点在直线段的同侧,直接返回点到线段起点的距离。如果投影大于等于线段长度,说明点在直线段的延长线上,直接返回点到线段终点的距离
if (proj < 0.0) {
*nearest_pt = start_;
return hypot(x0, y0);
}
if (proj > length_) {
*nearest_pt = end_;
return point.DistanceTo(end_);
}
*nearest_pt = start_ + unit_direction_ * proj;
// 计算点到线段的垂线与x轴正半轴的夹角,即x0 * unit_direction_.y() - y0 * unit_direction_.x(),取绝对值作为最终结果
return std::abs(x0 * unit_direction_.y() - y0 * unit_direction_.x());
}
rotate:逆时针旋转angle度(注意是弧度)
Vec2d LineSegment2d::rotate(const double angle) {
Vec2d diff_vec = end_ - start_;
diff_vec.SelfRotate(angle);
return start_ + diff_vec;
}
GetPerpendicularFoot:某个点到该线段垂点的距离
double LineSegment2d::GetPerpendicularFoot(const Vec2d &point,
Vec2d *const foot_point) const {
CHECK_NOTNULL(foot_point);
if (length_ <= kMathEpsilon) {
*foot_point = start_;
return point.DistanceTo(start_);
}
const double x0 = point.x() - start_.x();
const double y0 = point.y() - start_.y();
const double proj = x0 * unit_direction_.x() + y0 * unit_direction_.y();
*foot_point = start_ + unit_direction_ * proj;
return std::abs(x0 * unit_direction_.y() - y0 * unit_direction_.x());
}
1.2 包围盒
二维平面上,Box特指矩形包围盒。Planning模块经常将自车和障碍物抽象成一个矩形框,简化计算
bounding box
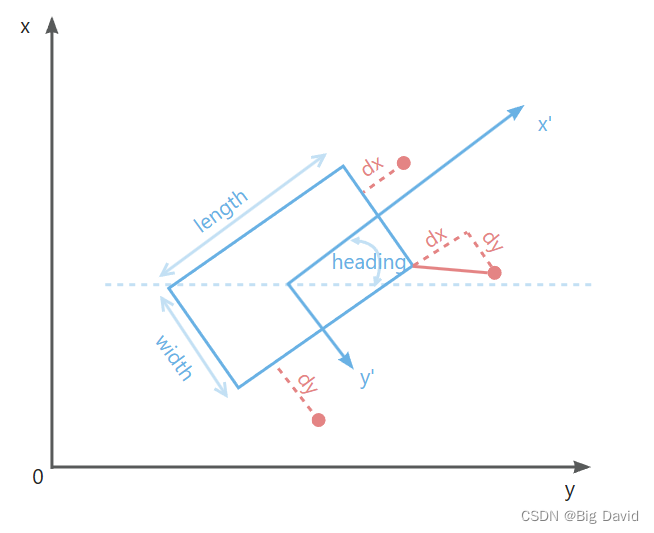
Box2d:普通矩形包围盒
文件路径:modules/common/math/box2d.h
IsPointIn函数检查给定点是否位于由其中心、方向、长度和宽度定义的二维框内
(1)首先计算点相对于长方体中心的x和y分量
(2)然后,它计算点与长方体沿x和y轴的距离,同时考虑长方体的航向。使用航向的余弦和正弦来计算距离。
(3)最后,如果两个距离都小于或等于长方体长度和宽度的一半,加上一个小的ε值(kMathEpsilon),则函数返回true。添加此ε值是为了说明潜在的舍入误差。如果任一距离大于长方体的一半长度或宽度,则函数返回false。
总体思路就是:
(1)以Box的Center为原点,heading方向为X’建立车身坐标系
(2)计算点在车身坐标系下的坐标
假设点的坐标
(
x
p
,
y
p
)
(x_p,y_p)
(xp,yp),Box中心坐标
(
x
c
,
y
c
)
(x_c,y_c)
(xc,yc),Box的heading角度
θ
\theta
θ,在局部坐标系下的坐标
[
d
x
d
y
]
=
[
c
o
s
θ
s
i
n
θ
−
s
i
n
θ
c
o
s
θ
]
[
x
p
−
x
0
y
p
−
y
0
]
\begin{bmatrix} dx\\ dy \end{bmatrix}=\begin{bmatrix} cos\theta & sin\theta\\ -sin\theta &cos\theta \end{bmatrix}\begin{bmatrix} x_p-x_0 \\ y_p-y_0 \end{bmatrix}
[dxdy]=[cosθ−sinθsinθcosθ][xp−x0yp−y0]
旋转矩阵是
[
c
o
s
θ
−
s
i
n
θ
s
i
n
θ
c
o
s
θ
]
\begin{bmatrix} cos\theta & -sin\theta\\ sin\theta &cos\theta \end{bmatrix}
[cosθsinθ−sinθcosθ]
(3)判断新坐标的x和y绝对值是否小于半个Box宽度和长度
bool Box2d::IsPointIn(const Vec2d &point) const {
const double x0 = point.x() - center_.x();
const double y0 = point.y() - center_.y();
const double dx = std::abs(x0 * cos_heading_ + y0 * sin_heading_);
const double dy = std::abs(-x0 * sin_heading_ + y0 * cos_heading_);
return dx <= half_length_ + kMathEpsilon && dy <= half_width_ + kMathEpsilon;
}
判断一个点是否在Boundary上,思路和上面的一样
bool Box2d::IsPointOnBoundary(const Vec2d &point) const {
const double x0 = point.x() - center_.x();
const double y0 = point.y() - center_.y();
const double dx = std::abs(x0 * cos_heading_ + y0 * sin_heading_);
const double dy = std::abs(x0 * sin_heading_ - y0 * cos_heading_);
return (std::abs(dx - half_length_) <= kMathEpsilon &&
dy <= half_width_ + kMathEpsilon) ||
(std::abs(dy - half_width_) <= kMathEpsilon &&
dx <= half_length_ + kMathEpsilon);
}
double DistanceTo(const Vec2d& point):计算Box到一个点的距离
(1)计算点在局部坐标系下的值
(2)如果
x
p
′
x^{'}_p
xp′绝对值小于半个车长,则直接用dy作为距离
(3)如果
y
p
′
y^{'}_p
yp′绝对值小于半个车宽,则直接用dx作为距离
其他情况,返回
d
x
2
+
d
y
2
\sqrt{dx^2+dy^2}
dx2+dy2,到角点的距离作为最终的距离
double Box2d::DistanceTo(const Vec2d &point) const {
const double x0 = point.x() - center_.x();
const double y0 = point.y() - center_.y();
const double dx =
std::abs(x0 * cos_heading_ + y0 * sin_heading_) - half_length_;
const double dy =
std::abs(x0 * sin_heading_ - y0 * cos_heading_) - half_width_;
if (dx <= 0.0) {
return std::max(0.0, dy);
}
if (dy <= 0.0) {
return dx;
}
return hypot(dx, dy);
}
1.3 多边形
不规则障碍物使用包围盒表示精度低,用多边形Polygon2d来抽象表示。
modules/common/math/polygon2d.h
多边形可以用多个点来表示,也可以用多个边来表示
std::vector<Vec2d> points_;
std::vector<LineSegment2d> line_segments_;
此函数用于从给定的一组点构建多边形
num_points_:多边形中的点数。
points_:Vec2d对象的矢量,表示多边形的点。
area_:多边形的面积。
line_segments_:LineSegment2d对象的矢量,表示连接多边形各点的线段。
is_convex_:一个布尔标志,指示多边形是否是凸的。
min_x_:多边形aabox的最小x值。
max_x_:多边形aabox的最大x值。
min_y_:多边形aabox的最小y值。
max_y_:多边形的aabox的最大y值。
void Polygon2d::BuildFromPoints() {
num_points_ = static_cast<int>(points_.size());
// 检查点的数量是否至少为3
CHECK_GE(num_points_, 3);
// 保证点顺时针
area_ = 0.0;
for (int i = 1; i < num_points_; ++i) {
// 使用连接每对点的向量的叉积来计算多边形的面积
area_ += CrossProd(points_[0], points_[i - 1], points_[i]);
}
// 如果面积为负值,则反转点的顺序,以确保它们按顺时针(ccw)顺序排列
if (area_ < 0) {
area_ = -area_;
std::reverse(points_.begin(), points_.end());
}
area_ /= 2.0;
CHECK_GT(area_, kMathEpsilon);
// 构建线段
line_segments_.reserve(num_points_);
// 通过迭代点并将每个点按ccw顺序连接到下一个点来构建线段向量
for (int i = 0; i < num_points_; ++i) {
line_segments_.emplace_back(points_[i], points_[Next(i)]);
}
// 检查凸性质
is_convex_ = true;
for (int i = 0; i < num_points_; ++i) {
// 通过计算连接前一点、当前点和下一点的向量的叉积来检查多边形是否是凸,如果叉积小于或等于-kMathEpsilon,则多边形不是凸的
if (CrossProd(points_[Prev(i)], points_[i], points_[Next(i)]) <=
-kMathEpsilon) {
is_convex_ = false;
break;
}
}
// 计算aabox.
// 最后,它通过找到点的最小值和最大值x和y来计算多边形的轴对齐边界框(aabox)
min_x_ = points_[0].x();
max_x_ = points_[0].x();
min_y_ = points_[0].y();
max_y_ = points_[0].y();
for (const auto &point : points_) {
min_x_ = std::min(min_x_, point.x());
max_x_ = std::max(max_x_, point.x());
min_y_ = std::min(min_y_, point.y());
max_y_ = std::max(max_y_, point.y());
}
}
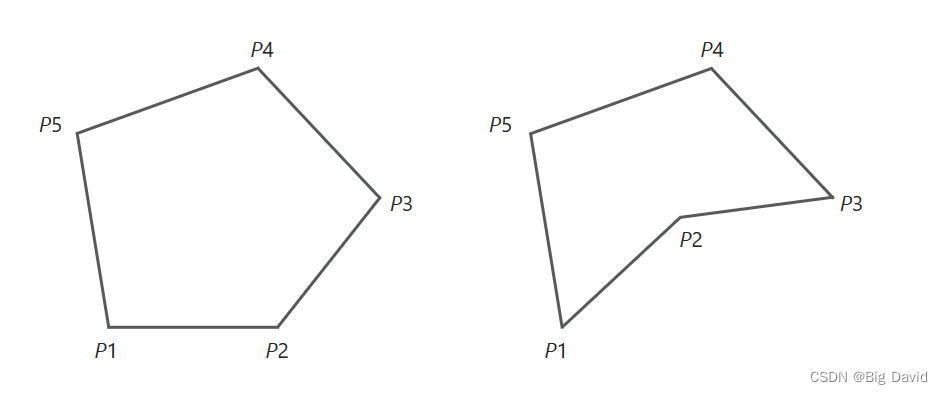
叉积(CrossProd)物理含义是向量组成的平行四边形的面积除以二就是三角形的面积,将所有三角形面积累加可以得到area_,如果area_为负数,说明角点按顺时针(CW)排列,需要进行reverse,从而保证所有的点是逆时针排列的CCW
如果连续的三个点
P
i
−
1
,
P
i
,
P
i
+
1
P_{i-1},P_i,P_{i+1}
Pi−1,Pi,Pi+1有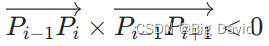
说明多边形非凸,比如右侧就是