题目链接

摆动排序 II

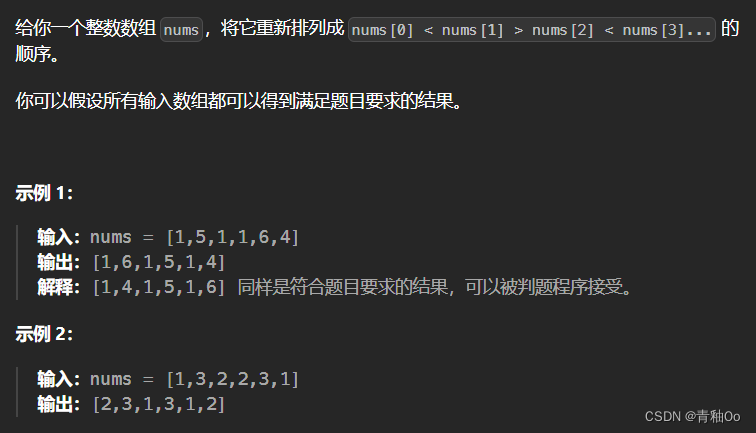
题目描述

注意点

• 将数组重新排列成 nums[0] < nums[1] > nums[2] < nums[3]… 的顺序
• 题目数据保证，对于给定的输入 nums ，总能产生满足题目要求的结果
• 用 O(n) 时间复杂度和 / 或原地 O(1) 额外空间来实现

解答思路

• 如果先将数组排序再进行摆动排序会非常简单，但是时间复杂度会达到O(nlogn)
• 参考题解可以先用快速排序将中位数找到，也就是在数组中间位置的元素，时间复杂度为O(n)，此时左侧数字都小于中位数，右侧数字都大于中位数，随后将左右侧元素交叉插入到数组中可以实现摆动排序
• 上述方法在某些特定情况下会错误，主要是有多个值相同的中位数时前后两段末尾处元素会相等，不是严格的摆动排序，所以还需要找到所有值等于中位数，将数组分为三部分（小于|等于|大于）
• 在分为三部分后，如果将左右侧元素交叉插入到数组仍然有可能会导致上面的问题，解决方法是从右往左先插入奇数下标，再插入偶数下标，保证数组是严格摆动排序

代码

class Solution {
    int n;
    int mid;
    public void wiggleSort(int[] nums) {
        n = nums.length;
        mid = (n - 1) / 2;
        // 快速排序找到中位数
        quickSort(nums, 0, n - 1);
        // 将等于中位数的数字都移动到数组中间
        int leftMedian = mid - 1;
        int rightMedian = mid + 1;
        for (int i = 0; i < leftMedian; i++) {
            if (nums[i] == nums[mid]) {
                swap(nums, i, leftMedian);
                leftMedian--;
            }
        }
        for (int i = n - 1; i > rightMedian; i--) {
            if (nums[i] == nums[mid]) {
                swap(nums, i, rightMedian);
                rightMedian++;
            }
        }
        int[] arr = Arrays.copyOf(nums, n);
        int idx = n - 1;
        // 从右到左先将写入奇数下标，再写入偶数下标
        for (int i = 1; i < n; i += 2) {
            nums[i] = arr[idx];
            idx--;
        }
        for (int i = 0; i < n; i += 2) {
            nums[i] = arr[idx];
            idx--;
        }
    }

    public void quickSort(int[] nums, int left, int right) {
        int idxLeft = left;
        int idxRight = right;
        while (idxLeft < idxRight) {
            if (nums[idxRight] > nums[left]) {
                idxRight--;
            } else if (nums[idxLeft] <= nums[left]) {
                idxLeft++;
            } else {
                swap(nums, idxLeft, idxRight);
            }
        }
        swap(nums, left, idxLeft);
        if (left == mid) {
            return;
        }
        if (idxLeft < mid) {
            quickSort(nums, idxLeft + 1, right);
        } 
        if (idxLeft > mid) {
            quickSort(nums, left, idxLeft - 1);
        }
    }

    public void swap(int[] nums, int left, int right) {
        int tmp = nums[left];
        nums[left] = nums[right];
        nums[right] = tmp;
    }
}

关键点

• 快速排序的思路
• 将数组按照小于|等于|大于的组合后，如何形成严格摆动排序的数组