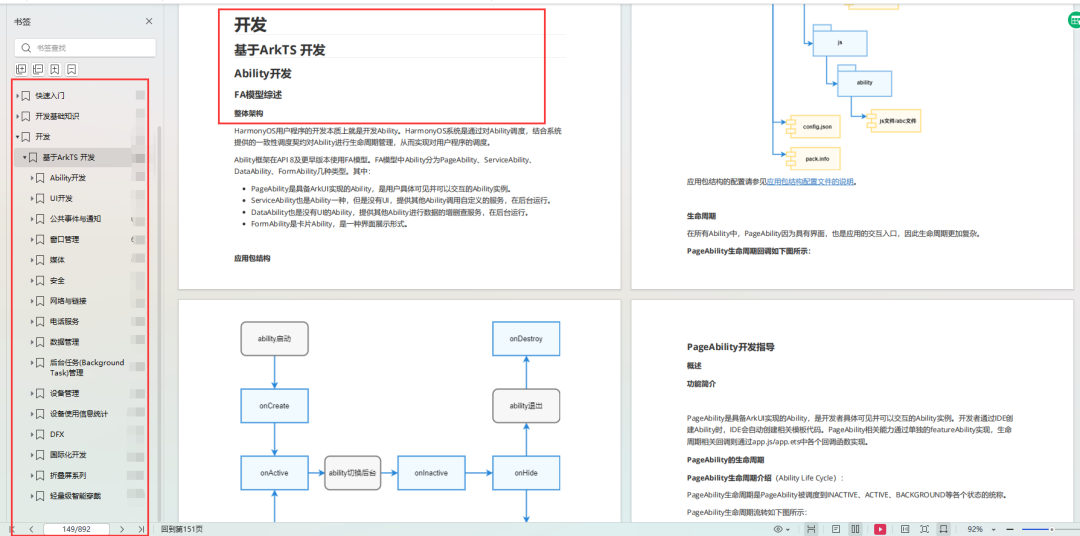
数据结构 | 二叉树入门
- 二叉树概念:
- 二叉树特点:
- 二叉树的基本形态
- 特殊二叉树
- 满二叉树
- 完全二叉树
- 二叉树的存储结构
- 二叉树的遍历
- 先序遍历
- 中序遍历
- 后序遍历
- 计算二叉树的节点个数
- 计算叶子节点的个数
- 树的高度
- 求第k层节点个数
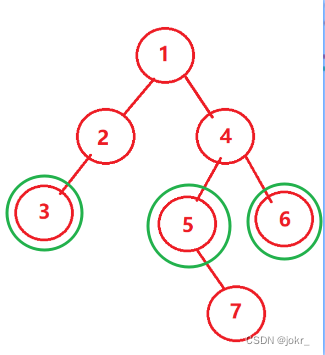
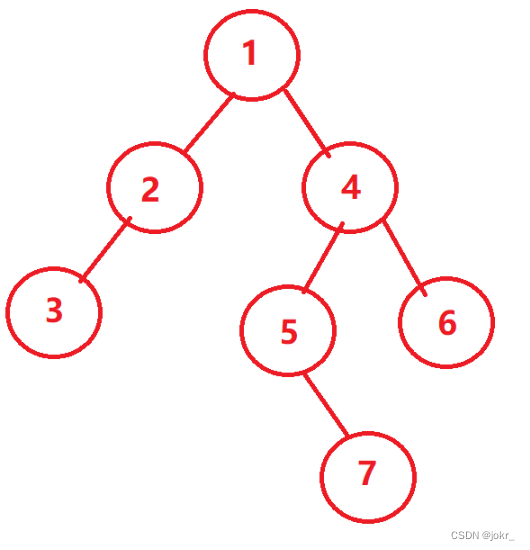
二叉树概念:
如下图,是一个二叉树,二叉树是一种特殊的树。
二叉树特点:
- 二叉树的每个节点都最多有
两棵树,所以二叉树的中不存在度大于2的节点。 - 二叉树的左右子树是有顺序的,次序不可颠倒
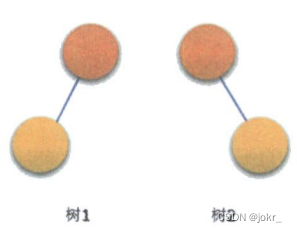
如图,树1 和 树2 就不是同一颗树。
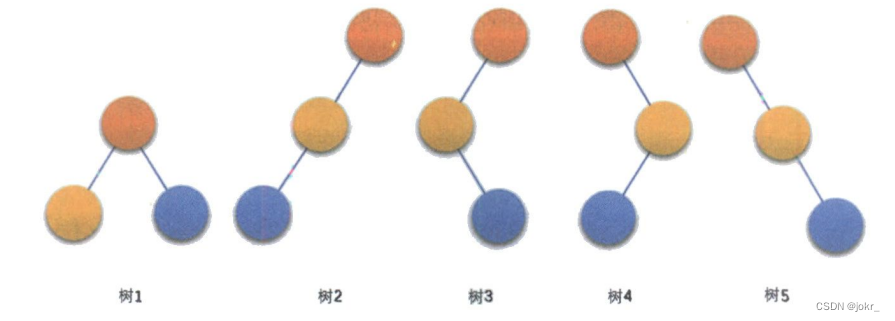
二叉树的基本形态
二叉树具有以下五种基本形态:
(1)空二叉树
(2)只有一个根结点。
(3)根结点只有左子树
(4)根结点只有右子树
(5)根结点既有左子树又有右子树
特殊二叉树
满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树并目所有叶子都在同
一层上,这样的二叉树称为满二叉树。
满二叉树:

完全二叉树
对于未满的<满二叉树> 并且从左到右连续的满二叉树称为完全二叉树。
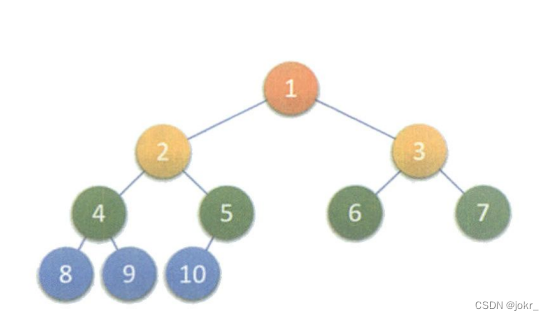
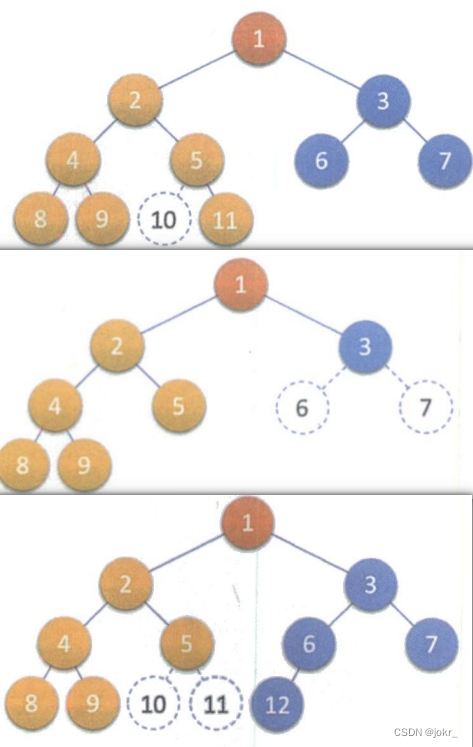
以下均不是完全二叉树:
二叉树的存储结构
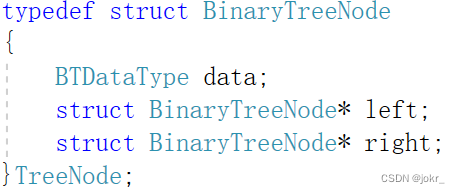
对于二叉树的存储一般采用链式存储:
二叉树每个结点最多有两个孩子,所以为它设计一个数据域和两个指针域是比较自然的想法,我们称这样的链表叫做二叉链表。

二叉树的遍历
先序遍历
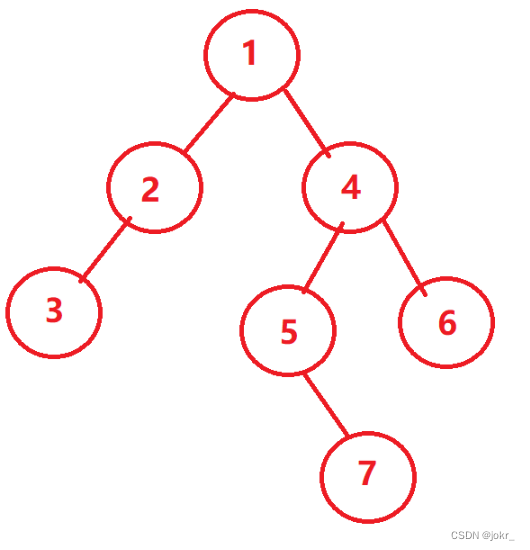
算法如下:

对于一般空的节点我们用N表示:
则这棵树的先序遍历为

//先序遍历
void PrevOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return 0;
}
printf("%d ", root->data);
PrevOrder(root->left);
PrevOrder(root->right);
}
递归示意图如下:
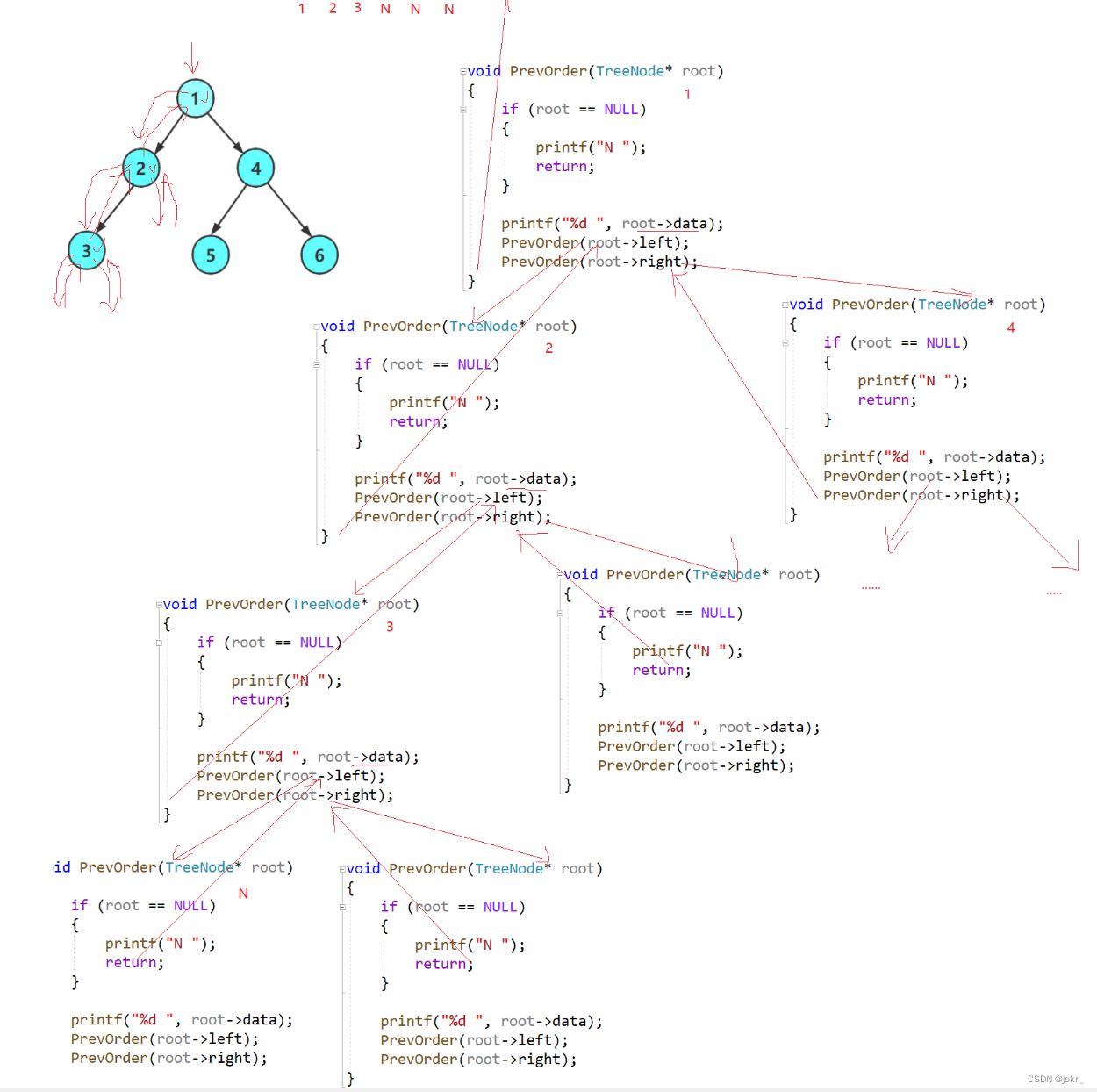
中序遍历

算法如下:

则这棵树的中序遍历为

//中序遍历
void InOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return 0;
}
InOrder(root->left);
printf("%d ", root->data);
InOrder(root->right);
}
后序遍历

算法如下

则这棵树的后序遍历:

代码:
//后序遍历
void PostOrder(TreeNode* root)
{
if (root == NULL)
{
printf("N ");
return 0;
}
InOrder(root->left);
InOrder(root->right);
printf("%d ", root->data);
}
计算二叉树的节点个数
顾名思义,计算一颗树的节点个数,传入该树的跟节点,采用分治的思路:

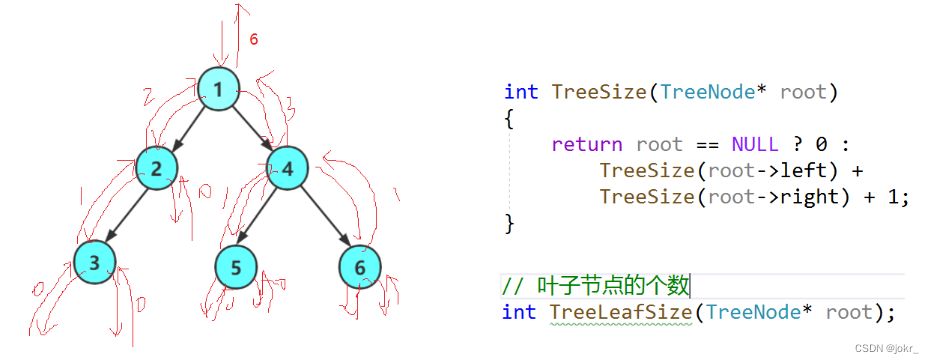
int TreeSize(TreeNode* root)
{
return root == NULL ? 0 : TreeSize(root->left) + TreeSize(root->right) + 1;
}

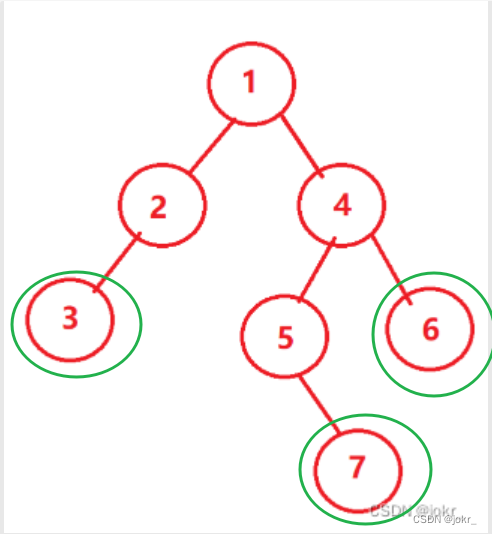
计算叶子节点的个数

递归图如下:
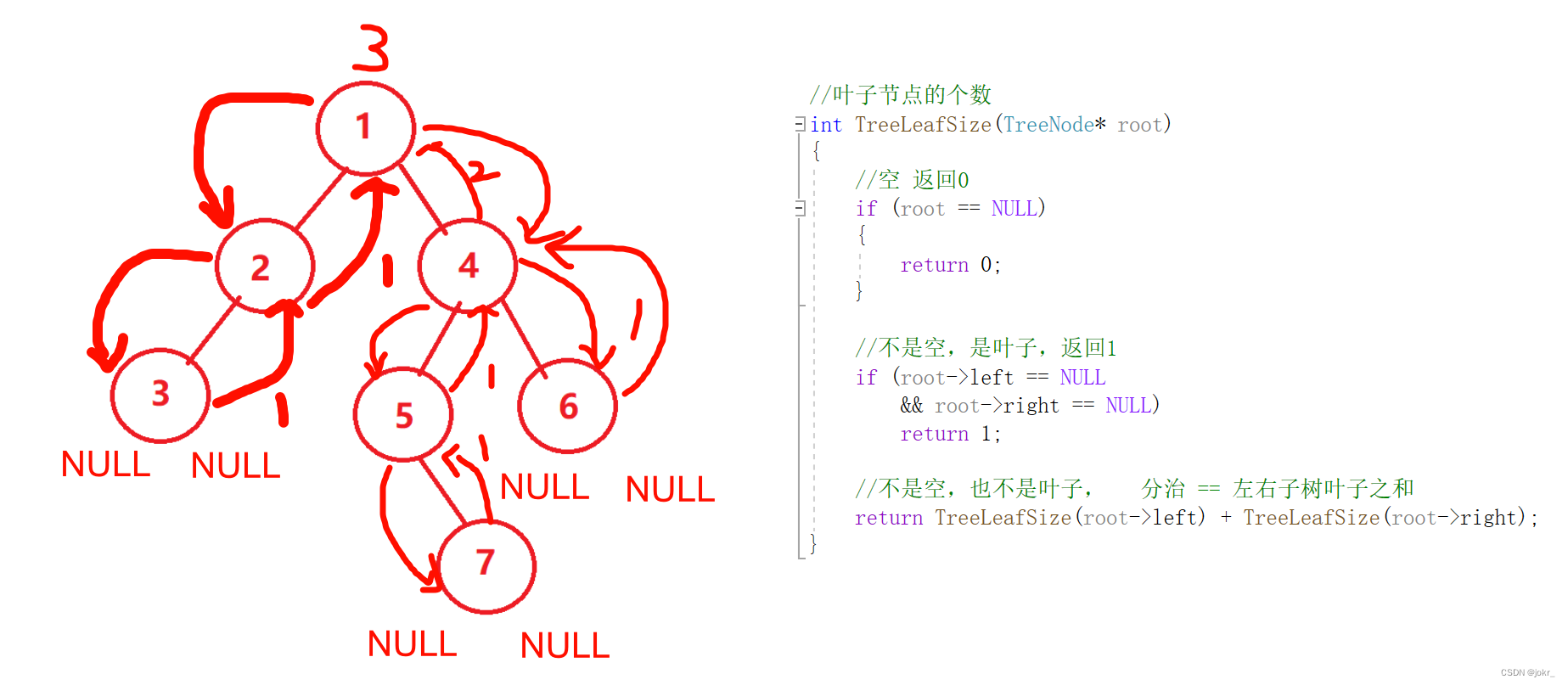
采用分治的思想,从root开始递归,有叶子节点就返回1,这个二叉树一共三个叶子节点,所以有返回3次1,相加得3.
//叶子节点的个数
int TreeLeafSize(TreeNode* root)
{
//空 返回0
if (root == NULL)
{
return 0;
}
//不是空,是叶子,返回1
if (root->left == NULL
&& root->right == NULL)
return 1;
//不是空,也不是叶子, 分治 == 左右子树叶子之和
return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

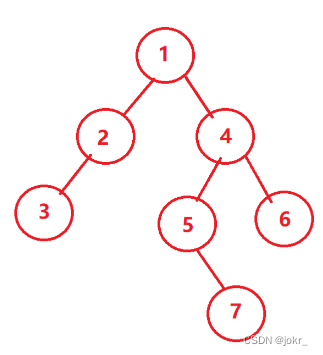
树的高度

递归图如下:

采用分治的思想:分别计算左数高度和右数高度,比较取最大。
代码如下:
//树的高度
int TreeHeight(TreeNode* root)
{
if (root == NULL)
return 0;
int leftHeight = TreeHeight(root->left);
int rightHeight = TreeHeight(root->right);
return leftHeight > rightHeight ? leftHeight + 1 : rightHeight + 1;
}

求第k层节点个数

递归图如下:

还是采用分治思想,当k=1时,返回一个节点数。
代码如下:
//第k层个数
int TreeLevelK(TreeNode* root, int k)
{
assert(k > 0);
if (root == NULL)
return 0;
if (k == 1)
return 1;
return TreeLevelK(root->left, k - 1) + TreeLevelK(root->right, k - 1);
}