人工神经网络（Artificial Neural Network，ANN）是指一系列受生物学和神经科学启发的数学模型．这些模型主要是通过对人脑的神经元网络进行抽象，构建人工神经元，并按照一定拓扑结构来建立人工神经元之间的连接，来模拟生物神经网络．在人工智能领域，人工神经网络也常常简称为神经网络（NeuralNetwork，NN）或神经模型。

神经网络最早是作为一种主要的连接主义模型。20 世纪 80 年代中后期，最流行的一种连接主义模型是分布式并行处理（Parallel Distributed Processing，PDP）模型，其有 3个主要特性：1）信息表示是分布式的（非局部的）；2）记忆和知识是存储在单元之间的连接上；3）通过逐渐改变单元之间的连接强度来学习新的知识。

连接主义的神经网络有着多种多样的网络结构以及学习方法，虽然早期模型强调模型的生物学合理性（Biological Plausibility），但后期更关注对某种特定认知能力的模拟，比如物体识别、语言理解等．尤其在引入误差反向传播来改进其学习能力之后，神经网络也越来越多地应用在各种机器学习任务上。随着训练数据的增多以及（并行）计算能力的增强，神经网络在很多机器学习任务上已经取得了很大的突破，特别是在语音、图像等感知信号的处理上，神经网络表现出了卓越的学习能力。

从机器学习的角度来看，神经网络一般可以看作一个非线性模型，其基本组成单元为具有非线性激活函数的神经元，通过大量神经元之间的连接，使得神经网络成为一种高度非线性的模型．神经元之间的连接权重就是需要学习的参数，可以在机器学习的框架下通过梯度下降方法来进行学习。

神经元

人工神经元（Artificial Neuron），简称神经元（Neuron），是构成神经网络的基本单元，其主要是模拟生物神经元的结构和特性，接收一组输入信号并产生输出。
生物学家在 20 世纪初就发现了生物神经元的结构．一个生物神经元通常具有多个树突和一条轴突．树突用来接收信息，轴突用来发送信息．当神经元所获得的输入信号的积累超过某个阈值时，它就处于兴奋状态，产生电脉冲．轴突尾端有许多末梢可以给其他神经元的树突产生连接（突触），并将电脉冲信号传递给其他神经元。

1943 年，心理学家 McCulloch 和数学家 Pitts 根据生物神经元的结构，提出了一种非常简单的神经元模型，MP神经元．现代神经网络中的神经元和 MP 神经元的结构并无太多变化．不同的是，MP 神经元中的激活函数𝑓 为0或1的阶跃函数，而现代神经元中的激活函数通常要求是连续可导的函数。

假设一个神经元接收𝐷 个输入𝑥1, 𝑥2, ⋯ , 𝑥𝐷，令向量𝒙 = [𝑥1; 𝑥2; ⋯ ; 𝑥𝐷]来表示这组输入，并用净输入（Net Input）𝑧 ∈ ℝ表示一个神经元所获得的输入信号𝒙的加权和。

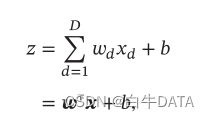
其中𝒘 = [𝑤1; 𝑤2; ⋯ ; 𝑤𝐷] ∈ ℝ𝐷 是𝐷 维的权重向量，𝑏 ∈ ℝ是偏置．净输入𝑧在经过一个非线性函数𝑓(⋅)后，得到神经元的活性值（Activation）𝑎，

𝑎 = 𝑓(𝑧)，

其中非线性函数𝑓(⋅)称为激活函数（Activation Function）。

图中给出了一个典型的神经元结构示例．

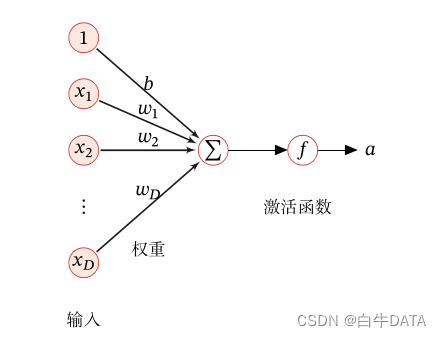
激活函数在神经元中非常重要的．为了增强网络的表示能力和学习能力，激活函数需要具备以下几点性质：

（1） 连续并可导（允许少数点上不可导）的非线性函数．可导的激活函数可以直接利用数值优化的方法来学习网络参数。

（2） 激活函数及其导函数要尽可能的简单，有利于提高网络计算效率。

（3） 激活函数的导函数的值域要在一个合适的区间内，不能太大也不能太小，否则会影响训练的效率和稳定性。