有题目:
循环队列放在一维数组A[0....M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初始时为空。下列判断队空和队满的条件中,正确的是 ( B )。
A.队空: end1 == end2;队满: end1 == (end2+1)mod M
B.队空: end1 == end2;队满: end2 == (end1+1)mod(M-1)
C.队空:end2 ==(end1+1)mod M;队满:end1==(end2+1)mod M
D.队空: end1==(end2+1)mod M;队满: end2 ==(end1+1)mod(M-1)
首先,什么是循环队列?
1、存储在首尾循环相接的向量空间中的队列即为循环队列。
循环队列的队空和队满情况
2、假设M为MaxSize最大容量,end1为头指针,指向队头元素;end2为尾指针,指向队尾元素的后一个位置
当循环队列为空时,end1==end2;当循环队列为满时,end1==end2;
为了区别这两种情况,规定:
① 循环队列最多只能有 M-1 个队列元素,当循环队列中只剩下一个空存储单元时,队列就已经满了。
② 初始值为空。
因此往往有两个结论:
循环队列判空的条件是end1==end2
循环队列判满的条件是end1==(end2+1)%M
那么这两个结论是怎么来的呢?
根据上面讲到的
因为循环队列最多只能有 M-1 个队列元素→故 M-1 那个点就是队尾元素
又因为end2为尾指针→故end2就是对应M-1 那个点
因为end1为头指针,又因为初始值为空,所以end1那个点记为null
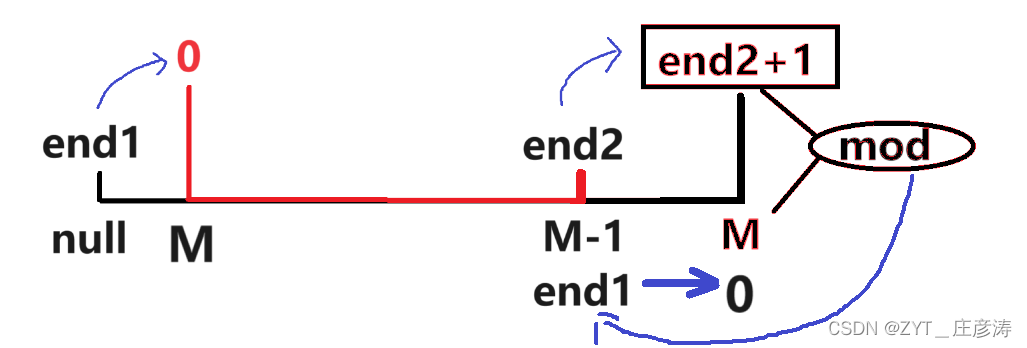
那么我们先根据这里讲的画出下面这张图:
因为end1指向队头元素,故我们假设队头元素为0(看下图)
又因为end2指向队尾元素的后一个位置,即end2+1,那么我们认为它移动了1个距离,由这个移动1个距离我们推出下面的就是M,也就是从左边 M-1 那移动了一个距离到这边 ,因此end2+1所在的点就是M所在的点。
所以根据下图的红色部分,因为我们上面的①说了:循环队列最多只能有 M-1 个队列元素,当循环队列中只剩下一个空存储单元时,队列就已经满了。
M与M-1之间刚好空出一个存储单元,故0到M-1这部分就已经属于队满的状态,而每一段的完整部分是0到M,本段的M就是下一段的0,这个先不理解,你看到本文最后就知道,其实本段的end2到下一段的end1更容易理解。
所以回到题目:
循环队列放在一维数组A[0....M-1]中,end1指向队头元素,end2指向队尾元素的后一个位置。假设队列两端均可进行入队和出队操作,队列中最多能容纳M-1个元素。初始时为空。下列判断队空和队满的条件中,正确的是 ( B )。
A.队空: end1 == end2;队满: end1 == (end2+1) mod M
B.队空: end1 == end2;队满: end2 == (end1+1) mod (M-1)
C.队空:end2 ==(end1+1)mod M;队满:end1==(end2+1) mod M
D.队空: end1==(end2+1)mod M;队满: end2 ==(end1+1) mod(M-1)=====================================================================
队空的情况我们很容易理解:
因为队空,所以end2==null;又因为循环队列是处于循环相接的环形向量之中,故end2即end1,故end1==end2,都是null
===================================================================== 队满的情况:
首先,我们要了解为什么循环队列要取模,即mod?
为了防止指针溢出,使指针的读写不超出队列的范围。
根据上面推导的图(即下图):
简单一点,根据箭头来判断就行:
0是仅仅接受end1即头指针来指向它,即end1会自然帮我们找到0;
end2+1仅仅接受end2即尾指针来指向它,即end2会自然帮我们找到end2+1
由前面我们已得到end1 == end2,因为向量空间要形成一个相接的环形,故肯定本段的end2就是下一段的end1,但这中间有一个隐藏的关于地址衔接的过程,这个隐藏过程里本来是end2去加1 即变成 end2+1 简简单单就可以找到下一段的头指针end1的地址了,从而end1会自然帮我们找到0,这是我们理所当然地想,但这样做的结果会造成指针溢出,造成错误,而取模就是防止指针溢出,所以在这个隐藏过程中我们修改一下,改让end2+1先去取模M后得出结果即end1的地址,此时算出来的end1的地址才是正确的地址,这样就不会指针溢出了,而且end1还能帮我们去指向0即队头元素。
也就是说, (end2+1) mod M结果才是end1的正确地址,即:
end1==(end2+1) mod M
这就是循环队列中
从本段end2到下一段的end1之间
隐藏的
关于地址衔接时寻找end1正确地址的过程
的
内容