基于MATLAB的均值，方差，变量的矩（附完整代码与例题）

news2024/11/14 21:34:33

一. 数学期望与方差

二. 样本的均值与方差

三. MATLAB代码

四. 例题与代码

4.1 正态分布

4.2 Rayleigh分布

五. 随机变量的矩

5.1 原点矩与中心距

5.2 例题3

5.3 样本向量的原点矩与中心矩

一. 数学期望与方差

将某连续随机变量x的概率密度函数记为p(x)，其数学期望E[x]可计算为：

$E[x]=\int_{-\infty}^\infty xp(x)dx$

更进一步，方差D[x]可计算为：

$D[x]=\int_{-\infty}^{\infty}(x-E[x])^2p(x)dx$

二. 样本的均值与方差

在实际中测出的一组样本数据写做：

$x_1,x_2,x_3,\cdots,x_n$

该样本的均值计算为：

$\bar x=\frac{1}{n}\sum_{i=1}^nx_i$

样本的方差计算为：

$\hat s_x^2=\frac{1}{n}\sum_{i=1}^n(x_i-\bar x)^2$

其实这个方差用的并不多，更多用的是无偏方差，如下:

$s_x^2=\frac{1}{n-1}\sum_{i=1}^n(x_i-\bar x)^2$

注意分母位置为n-1，开根号后叫标准差。

为了方便表示，一组随机变量样本数据构成的向量，可以写做：

$x=[x_1,x_2,x_3,\cdots,x_n]^T$

注意通常为列向量。

三. MATLAB代码

求样本向量各个元素的均值使用代码：

m=mean(x)

求方差使用代码：

s2=var(x)

求标准差使用代码：

s=std(x)

四. 例题与代码

4.1 正态分布

例题1

生成一组3000个正态分布随机数，使其均值为0.5，标准差为1.5。

（1）分析数据实际的均值，方差和标准差

（2）如果减小样本个数，会有什么结果？

解：

MATLAB代码：

clear;
clc;
close all;

p=normrnd(0.5,1.5,30000,1); %normrnd正态分布的随机数
%0.5代表均值，1.5代表方差，30000和1代表30000行1列的数据
[mean(p),var(p),std(p)]
%mean计算均值，var计算方差,std计算标准差


%选择30个随机数
p=normrnd(0.5,1.5,30,1);
[mean(p),var(p),std(p)]

运行结果：

ans =0.5048 2.2441 1.4980

ans =0.3707 2.5184 1.5870

可见在进行较精确的统计分析时不能选择太小的样本点

4.2 Rayleigh分布

在分布类型标识的后面加后缀stat，可以直接求该分布的均值和方差。比如来看一个例题。

例题2

假定Rayleigh分布的参数b=0.45，求其均值与方差。

五. 随机变量的矩

5.1 原点矩与中心距

假定x为某连续随机变量，且p(x)为其概率密度函数。则该变量的r阶原点矩定义为：

可以发现一阶的原点矩就是均值，也就是：

$v_1=E[x]$

该变量的r阶中心矩定义为：

$\mu_r=\int_{-\infty}^\infty (x-\mu)^rp(x)dx$

很明显可以发现2阶中心矩就是方差，也就是：

$\mu_2=D[x]$

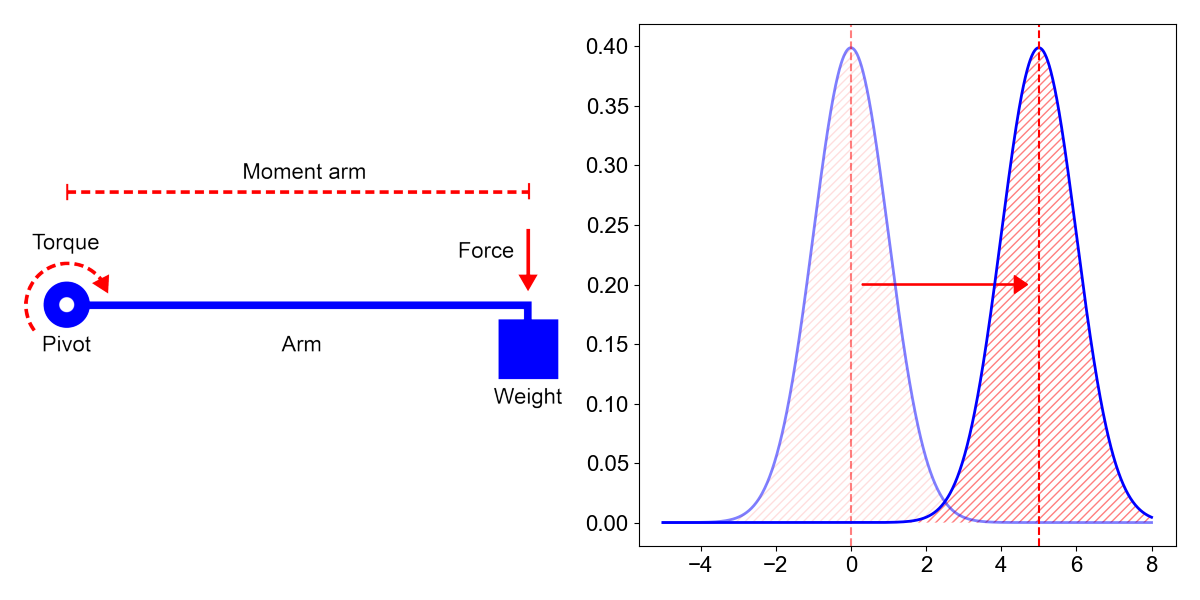
放一张跟正态分布相关的矩的图：

5.2 例题3

考虑 $\Gamma$ 分布 $(a>0,\lambda>0)$ 的原点矩和中心矩，并由前几项总结规律。

推荐阅读：

基于MATLAB的泊松分布，正态分布与伽玛分布（附完整代码与例题）-CSDN博客

解：

计算原点矩的MATLAB代码：

clear;
clc;
close all;

%求解原点矩
syms x; 
syms a lam positive;
p=lam^a*x^(a-1)/gamma(a)*exp(-lam*x);
for n=1:5
    m=int(x^n*p,x,0,inf)
end

运行结果：

m =a/lam

m =(a*(a + 1))/lam^2

m =(a*(a^2 + 3*a + 2))/lam^3

m =(a*(a^3 + 6*a^2 + 11*a + 6))/lam^4

m =(a*(a^4 + 10*a^3 + 35*a^2 + 50*a + 24))/lam^5

很明显有规律

计算中心矩的MATLAB代码：

%计算中心矩
syms n; 
syms x; 
syms a lam positive; 
p=lam^a*x^(a-1)/gamma(a)*exp(-lam*x);
for n=1:6
    s=simplify(int((x-1/lam*a)^n*p,x,0,inf))
end

运行结果：
s =0

s =(lam^(a - 2)*int(x^(a - 1)*exp(-lam*x)*(a - lam*x)^2, x, 0, Inf))/gamma(a)

s =-(lam^(a - 3)*int(x^(a - 1)*exp(-lam*x)*(a - lam*x)^3, x, 0, Inf))/gamma(a)

s =(lam^(a - 4)*int(x^(a - 1)*exp(-lam*x)*(a - lam*x)^4, x, 0, Inf))/gamma(a)

s =-(lam^(a - 5)*int(x^(a - 1)*exp(-lam*x)*(a - lam*x)^5, x, 0, Inf))/gamma(a)

s =(lam^(a - 6)*int(x^(a - 1)*exp(-lam*x)*(a - lam*x)^6, x, 0, Inf))/gamma(a)

整体来看中心矩无规律

5.3 样本向量的原点矩与中心矩

在网络安全等领域，我们需要根据样本来估计分布。比如，给定某随机数的一些样本点，如下：

$x_1,x_2,x_3,\cdots,x_n$

该随机变量的r阶原点矩计算为：

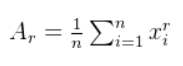
该随机变量的r阶中心矩计算为：

利用MATLAB代码可直接计算随机变量x的r阶原点矩与中心矩：

%r阶原点矩
Ar=sum(x.^r)/length(x)
%注意x后面有一个点，length函数可以求向量x中的元素个数

%r阶中心矩
Br=moment(x,r)

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1364806.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！