步骤一:定义一个二叉树的节点类
定义一个二叉树的节点类,其中包含节点的值、左子节点和右子节点。
// 二叉树节点定义
public class TreeNode
{
public int Value { get; set; } // 节点的值
public TreeNode Left { get; set; } // 左子节点
public TreeNode Right { get; set; } // 右子节点
public TreeNode(int value)
{
Value = value;
}
}
步骤二:定义一个二叉树类
我们定义一个二叉树类,其中包含了三种遍历方式的方法。
public class BinaryTree
{
// 前序遍历
public void PreorderTraversal(TreeNode root)
{
//相关代码
}
// 中序遍历
public void InorderTraversal(TreeNode root)
{
//相关代码
}
// 后序遍历
public void PostorderTraversal(TreeNode root)
{
//相关代码
}
}
步骤三 三种遍历方法
前序遍历
前序遍历:从根节点开始,先输出节点值,再依次将右子节点和左子节点压入栈中。
// 前序遍历
public void PreorderTraversal(TreeNode root)
{
if (root == null)
return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 定义一个栈
stack.Push(root); // 将根节点压入栈中
Console.Write("前序遍历");
while (stack.Count > 0) // 当栈不为空时
{
TreeNode node = stack.Pop(); // 弹出栈顶节点
Console.Write(node.Value + " "); // 输出节点值
if (node.Right != null) // 若有右子节点,则将其压入栈中
stack.Push(node.Right);
if (node.Left != null) // 若有左子节点,则将其压入栈中
stack.Push(node.Left);
}
}
中序遍历
中序遍历:从根节点开始,先将当前节点及其左子节点全部压入栈中,然后弹出栈顶节点并输出节点值,最后处理右子节点。
// 中序遍历
public void InorderTraversal(TreeNode root)
{
if (root == null)
return;
Stack<TreeNode> stack = new Stack<TreeNode>(); // 定义一个栈
TreeNode current = root;
Console.Write("中序遍历");
while (current != null || stack.Count > 0) // 当节点不为空或栈不为空时
{
while (current != null) // 将当前节点及其左子节点全部压入栈中
{
stack.Push(current);
current = current.Left;
}
current = stack.Pop(); // 弹出栈顶节点
Console.Write(current.Value + " "); // 输出节点值
current = current.Right; // 处理右子节点
}
}
后序遍历
后序遍历:从根节点开始,先将根节点和其左右子节点依次压入第一个栈中,然后将第一个栈中的节点依次弹出并压入第二个栈中,最后依次弹出第二个栈中的节点并输出节点值。
// 后序遍历
public void PostorderTraversal(TreeNode root)
{
if (root == null)
return;
Stack<TreeNode> stack1 = new Stack<TreeNode>(); // 定义两个栈
Stack<TreeNode> stack2 = new Stack<TreeNode>();
stack1.Push(root); // 将根节点压入第一个栈中
Console.Write("后序遍历");
while (stack1.Count > 0) // 当第一个栈不为空时
{
TreeNode node = stack1.Pop(); // 弹出栈顶节点
stack2.Push(node); // 将节点压入第二个栈中
if (node.Left != null) // 若有左子节点,则将其压入第一个栈中
stack1.Push(node.Left);
if (node.Right != null) // 若有右子节点,则将其压入第一个栈中
stack1.Push(node.Right);
}
while (stack2.Count > 0) // 当第二个栈不为空时
{
TreeNode node = stack2.Pop(); // 弹出栈顶节点
Console.Write(node.Value + " "); // 输出节点值
}
}
前序遍历:从根节点开始,先输出节点值,再依次将右子节点和左子节点压入栈中。
步骤四 使用
在主函数中构建一个二叉树,并调用上面定义的三种遍历方法进行遍历。
static void Main(string[] args)
{
// 构建一个二叉树
TreeNode root = new TreeNode(1); // 根节点
root.Left = new TreeNode(2); // 左子节点
root.Right = new TreeNode(3); // 右子节点
root.Left.Left = new TreeNode(4); // 左子节点的左子节点
root.Left.Right = new TreeNode(5); // 左子节点的右子节点
// 创建 BinaryTree 对象
BinaryTree binaryTree = new BinaryTree();
binaryTree.PreorderTraversal(root); //进行前序遍历
binaryTree.InorderTraversal(root);//进行中序遍历
binaryTree.PostorderTraversal(root);//进行后序遍历
}

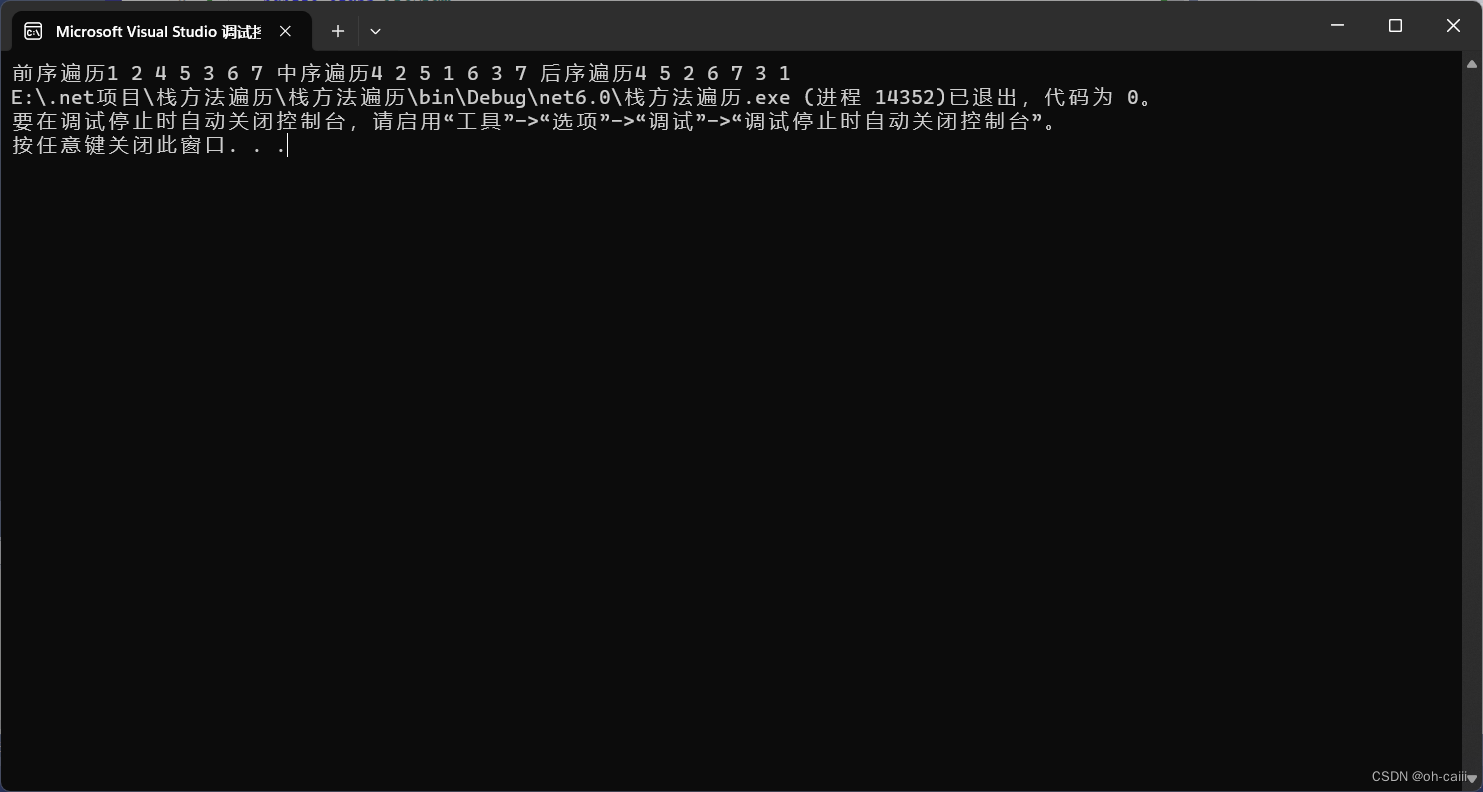
步骤五 运行结果