测量
测量的定义
以确定被测量对象量值为目的的操作称作测量。
测量的过程就是把被测物理量与选作计量单位的同类物理量进行比较的过程。
测量值的组成
物理量的测量值由数值和单位两部分组成。
测量的分类
测量分直接测量与间接测量。
等精度测量：对某一物理量多次重复测量时，测量条件不变。不存在绝对等精度测量。
不等精度测量：对某一物理量多次重复测量时，测量条件部分或完全改变。
基本单位
长度（米.m）、 质量（千克.kg） 、时间（秒.s）、电流强度（安培.A）、热力学温标（开尔文.K）、物质的量（摩尔.mol）、发光强度（坎德拉.cd）
真值与实际值
真值是被测量所具有的真实大小，是理想概念。
实际值是和真值接近、满足规定准确度，用来代替真值的近真值。
测量结果的完整表述
误差取1~2位，平均值最后一位与误差位对齐
误差
误差的定义
误差 = 测量值 - 真值
理论上无穷次等精度测量的结果的算数平均最接近真值。
误差的分类
系统误差
具有可预测性。
按对于其的掌握程度分为已定和未定：对于已定系统误差，我们已经掌握其数值与符号的规律；而对于未定，我们未确切掌握，比如可能是掌握数值但未掌握符号。例如电表的系统误差（可以估计其误差限）。
已定系统误差可以消除。
关于误差限
偶然误差
服从统计规律
粗大误差
如人为读数错误等，应剔除。
测量不确定度
测量不确定度是一个与测量结果关联的参数，用以表征合理赋予被测量值的分散性，体现结果的可信赖程度。
标准不确定度u
用标准误差表示的测量不确定度
按其数值评定方法分为：A类不确定度和B类不确定度
A类不确定度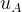
由观测列统计分析所得，又称统计不确定度。
B类不确定度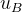
由不同于观测列统计分析所得，又称非统计不确定度。
合成标准不确定度
由几个不确定度分量影响的测量结果的标准不确定度，由分量的方差或协方差相加所得，记为。
相对合成标准不确定度
其中 y 可以是测量值、平均值、理论值等。
不确定度和误差的对比
都是精度评定参数。
系统和偶然误差引起不确定度，是不确定度的基础。
误差以真值为中心，不确定度以估计值为中心。
误差难定量，不确定度可定量。
直接测量不确定度的评定
对于物理量X做n次等精度测量，测量结果为，计算其算数平均值
现在考虑：粗大误差需要剔除，系统误差可以消除或者减弱，因此主要考虑随机误差的影响。
随机误差分布
随机误差呈正态分布，其概率方程：
其中，有
随机误差的大小由标准误差表示
置信区间：误差出现在区间内的概率
A类不确定度的评定
即为
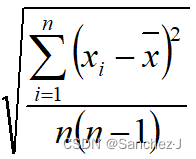
对于有限次测量，应保证同样的不确定度，A类不确定度为其中
因子和置信概率与测量次数有关。
B类不确定度测量
B类不确定度有多项分量，如读数误差、仪器误差等，大学物理主要考虑仪器误差，仪器误差多服从均匀分布。
其中仪为仪器最大允许误差，
为置信因子（与置信概率相关），C为置信系数（与误差分布特性有关）
仪 = 量程 × 级别 / 100
不知级别时，通常取最小分度值的一般。
对于单次测量，只有B类不确定度
两类不确定度的合成
直接测量的合成标准不确定度：
直接测量不确定度结果表示：
间接测量不确定度的评定
间接测量量，由直接测量不确定度传递。
其中，各直接测量结果为：
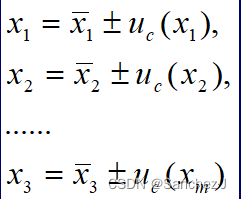
y的标准测量不确定度公式
y的相对测量不确定度公式
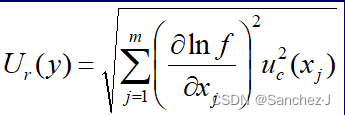
且有
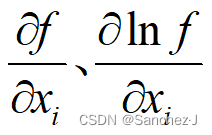为不确定度传递系数
结果表达：
或
推导举例
和差函数直接求
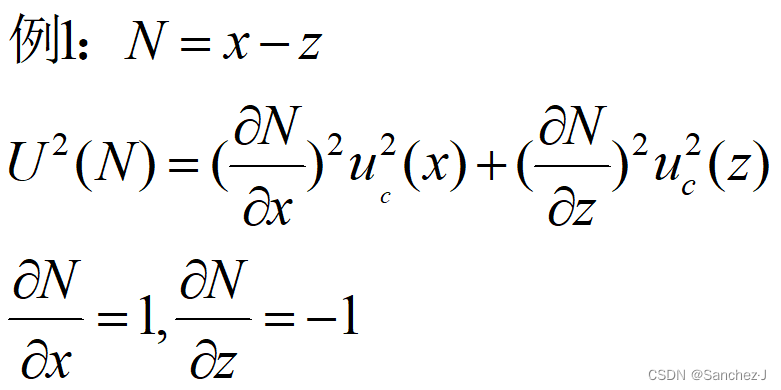
积商函数先取对数求相对标准不确定度
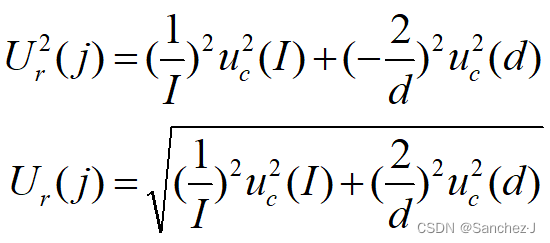
有效数字规定
测量值一般只保留一位欠准确数。
有效位数：左起第一位非零数字起，到第一位欠准确数止的全部数位。
有效数字与小数点位置和单位无关，改变单位时有效位数不变
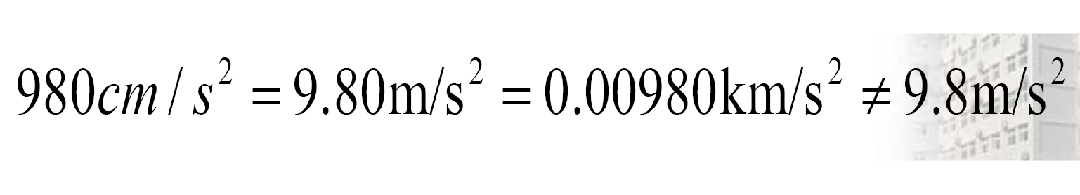
运算中的有效数字
准确与准确得准确
准确与欠准确得欠准确（但进位是准确）
运算结果只保留一位欠准确数字，去掉第二位欠准确数字时不是采用四舍五入，其方法如下：
欲舍弃数字不等于5时，小于5舍，大于5进位；
欲舍弃数字等于5时，欲保留数字为奇数则进，为偶数则舍。
加减
乘除
开方
有效位数与其底的有效位数相同
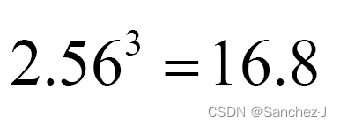
乘方
结果表述中不确定度一般取1位有效数字，相对不确定度取1到2位有效数字，测量值有效数字尾数与不确定度尾数应对齐。
