84.柱状图中最大的矩形：

题目链接
给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。
求在该柱状图中，能够勾勒出来的矩形的最大面积。

示例 :

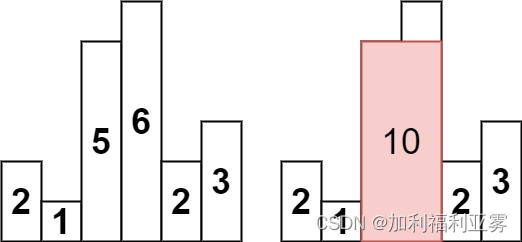
输入：heights = [2,1,5,6,2,3]
输出：10
解释：最大的矩形为图中红色区域，面积为 10

解答：

class Solution {
    int largestRectangleArea(int[] heights) {
        Stack<Integer> st = new Stack<Integer>();
        
        // 数组扩容，在头和尾各加入一个元素
        int [] newHeights = new int[heights.length + 2];
        newHeights[0] = 0;
        newHeights[newHeights.length - 1] = 0;
        for (int index = 0; index < heights.length; index++){
            newHeights[index + 1] = heights[index];
        }

        heights = newHeights;
        
        st.push(0);
        int result = 0;
        // 第一个元素已经入栈，从下标1开始
        for (int i = 1; i < heights.length; i++) {
            // 注意heights[i] 是和heights[st.top()] 比较 ，st.top()是下标
            if (heights[i] > heights[st.peek()]) {
                st.push(i);
            } else if (heights[i] == heights[st.peek()]) {
                st.pop(); // 这个可以加，可以不加，效果一样，思路不同
                st.push(i);
            } else {
                while (heights[i] < heights[st.peek()]) { // 注意是while
                    int mid = st.peek();
                    st.pop();
                    int left = st.peek();
                    int right = i;
                    int w = right - left - 1;
                    int h = heights[mid];
                    result = Math.max(result, w * h);
                }
                st.push(i);
            }
        }
        return result;
    }
}

算法总结：

本题整体思路实际上和上一题接雨水的思路是一样的，唯一不同的是接雨水我们希望求比当前柱子更低的柱子，而本题我们要求更高的柱子，所以在单调栈判断入栈上的处理上不同，即heights[i] > heights[st.peek()]时，当前元素入栈。