java数据结构与算法刷题-----LeetCode63. 不同路径 II

news2025/1/12 3:02:20

java数据结构与算法刷题目录（剑指Offer、LeetCode、ACM）-----主目录-----持续更新(进不去说明我没写完)：`https://blog.csdn.net/grd_java/article/details/123063846`

很多人觉得动态规划很难，但它就是固定套路而已。其实动态规划只不过是将多余的步骤，提前放到dp数组中（就是一个数组，只不过大家都叫它dp），达到空间换时间的效果。它仅仅只是一种优化思路，因此它目前的境地和线性代数一样----虚假的难。

想想线性代数，在国外留学的学生大多数不觉得线性代数难理解。但是中国的学生学习线性代数时，完全摸不着头脑，一上来就是行列式和矩阵，根本不知道这玩意是干嘛的。
线性代数从根本上是在空间上研究向量，抽象上研究线性关系的学科。人家国外的教科书都是第一讲就帮助大家理解研究向量和线性关系。
反观国内的教材，直接把行列式搞到第一章。搞的国内的学生在学习线性代数的时候，只会觉得一知半解，觉得麻烦，完全不知道这玩意学来干什么。当苦尽甘来终于理解线性代数时干什么的时候，发现人家国外的教材第一节就把这玩意讲清楚了。你只会大骂我们国内这些教材，什么狗东西（以上是自己学完线性代数后的吐槽，我们同学无一例外都这么觉得）。

而我想告诉你，动态规划和线性代数一样，我学完了才知道，它不过就是研究空间换时间，提前将固定的重复操作规划到dp数组中，而不用暴力求解，从而让效率极大提升。

但是网上教动态规划的兄弟们，你直接给一个动态方程是怎么回事？和线性代数，一上来就教行列式和矩阵一样，纯属恶心人。我差不多做了30多道动态规划题目，才理解，动态方程只是一个步骤而已，而这已经浪费我很长时间了，我每道题都一知半解不理解，过程及其痛苦。最后只能重新做。
动态规划，一定是优先考虑重复操作与dp数组之间的关系，搞清楚后，再提出动态方程。而你们前面步骤省略了不讲，一上来给个方程，不是纯属扯淡吗？
我推荐研究动态规划题目，按5个步骤，从上到下依次来分析

DP数组及下标含义
递推公式
dp数组初始化
数组遍历顺序（双重循环及以上时，才考虑）
dp数组打印，分析思路是否正确（相当于做完题，检查一下）

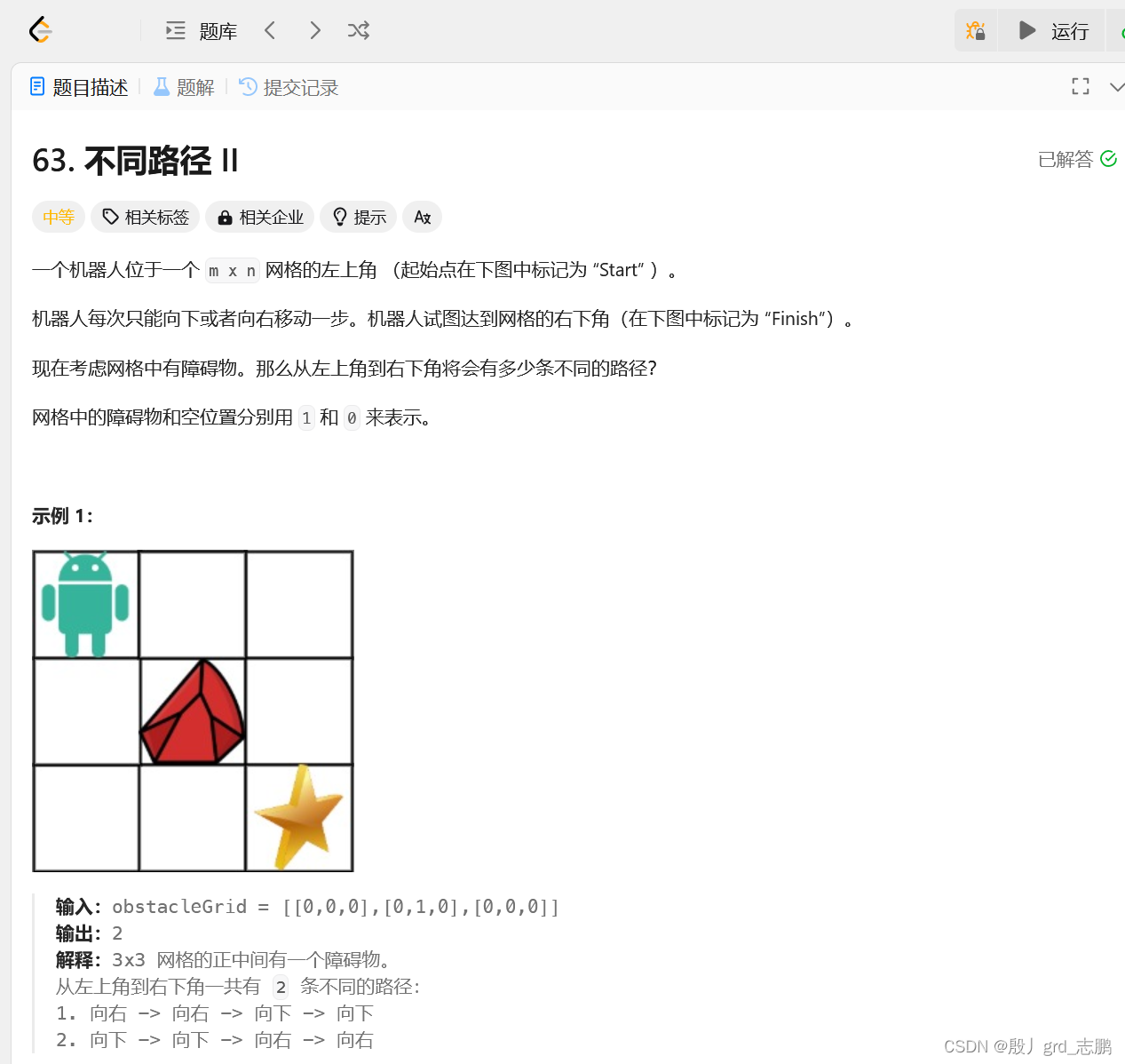
这道题是62题的衍生题，在62题的基础上，增加了一个条件，就是路上会有障碍物，导致涉及这个障碍物的路无法通行。对应到代码就是加了一个if语句罢了。除此之外没有任何不同

可以先参考🏆LeetCode62. 不同路径`https://blog.csdn.net/grd_java/article/details/135421514`

先理解题目细节

机器人只能向右或向下走，也就是说，我们到达每一个方格，只有两种情况，从上面过来的，或者从左面过来的。注意区分“走过去”和“从哪过来的区别”，这是解出这道题的关键。
所以与其考虑到达终点有几条路可以走，不如考虑到这个位置，可以从哪里来。
要特别注意，第一行和第一列，如果到某个位置的中间有障碍物，那么就只能是0. 因为第一行和第一列，没有障碍物的情况下，也只有一条路可以到达，如果中间堵了，肯定就到不了。

解题思路

暴力求解的思想，就是回溯算法，枚举每一种情况，拿到最大值，显然会做大量无效运算。
但是如果我们预先将其存储到dp数组，就可以直接通过dp[x], 获取dp数组中指定位置x的体力花费，而不用枚举。典型的动态规划题目

动态规划思考5步曲

DP数组及下标含义

我们要求出的是到达某个方块，可以从哪里过来，过来的方法有几种，那么dp数组中存储的就是到达这里有几种方法可以过来。要求出谁的可到达方法的数量呢？显然是某个方块，那么下标就是代表现在到了哪个方块，也就是代表到了某一方块后的可以过来的路。显然，需要2个下标表示，故这道题的dp数组需要二维数组

递推公式

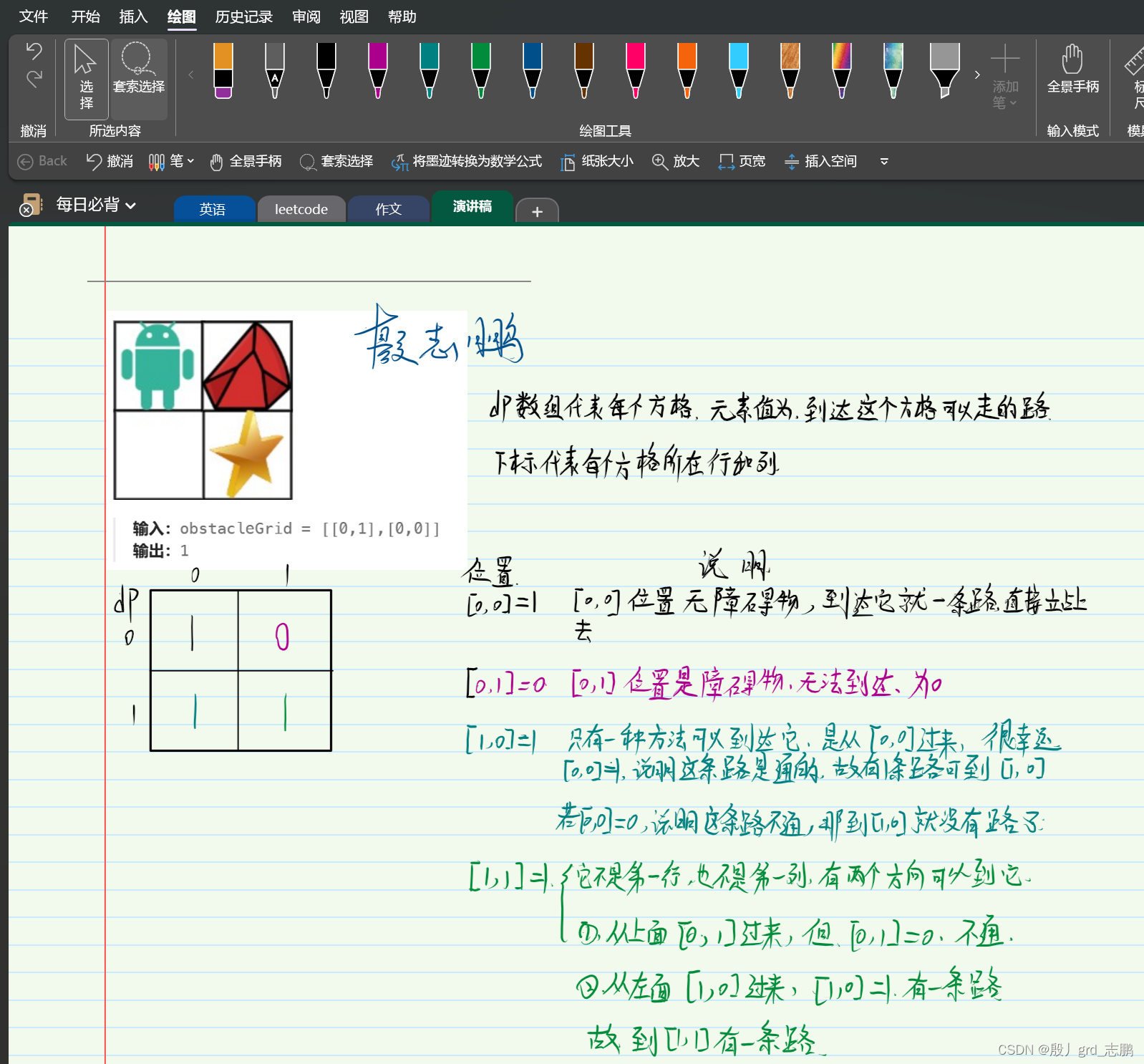
由题意可知，只能选择向右走或者向下走，因此对于每个方块而言，只能是从上面过来，或者从左面过来。而第一行没有从上面来的路，因此只能从左面过来，也就是第一行都只有一条从左面来的路，没有障碍物的情况下都是1。同理第一列，没有从左面来的路，只能从上面过来，没有障碍物的情况下也只有从上面过来这一条路。

故：第一行和第一列没有障碍物情况下都固定为1，F(0,n) = 1; F(n,0) = 1
如果有障碍物，说明这条路不通，只能是0. 我们只需要看前一个位置通不通，就能判断当前位置通不通。F(0,n) = f(0,n-1)==0?0:1. F(n,0) = f(n-1,0)==0?0:1.

之后每一个方块，都需要考虑从上面来的路有几条，从左面来的路有几条。也就是到它上面的方块有几条路+到它左面的方块有几条路
因此，可以得到，从第二行，第二列开始，递推公式变为，到左边方块的路+到上面方块的路。F(n,n) = F(n-1,n)+F(n,n-1)

dp数组初始化

数组遍历顺序

双重循环，我们知道这道题，数组下标表示方块的位置，也就是所在行和列的位置。那么其中一层循环代表第几行，另外一层循环代表第几列。那么先遍历行还是列呢？我们发现，无论遍历哪个，都不影响。我们可以一列一列考虑，也可以一行一行考虑，因此，先遍历哪个都一样。我们这里选择先遍历行。

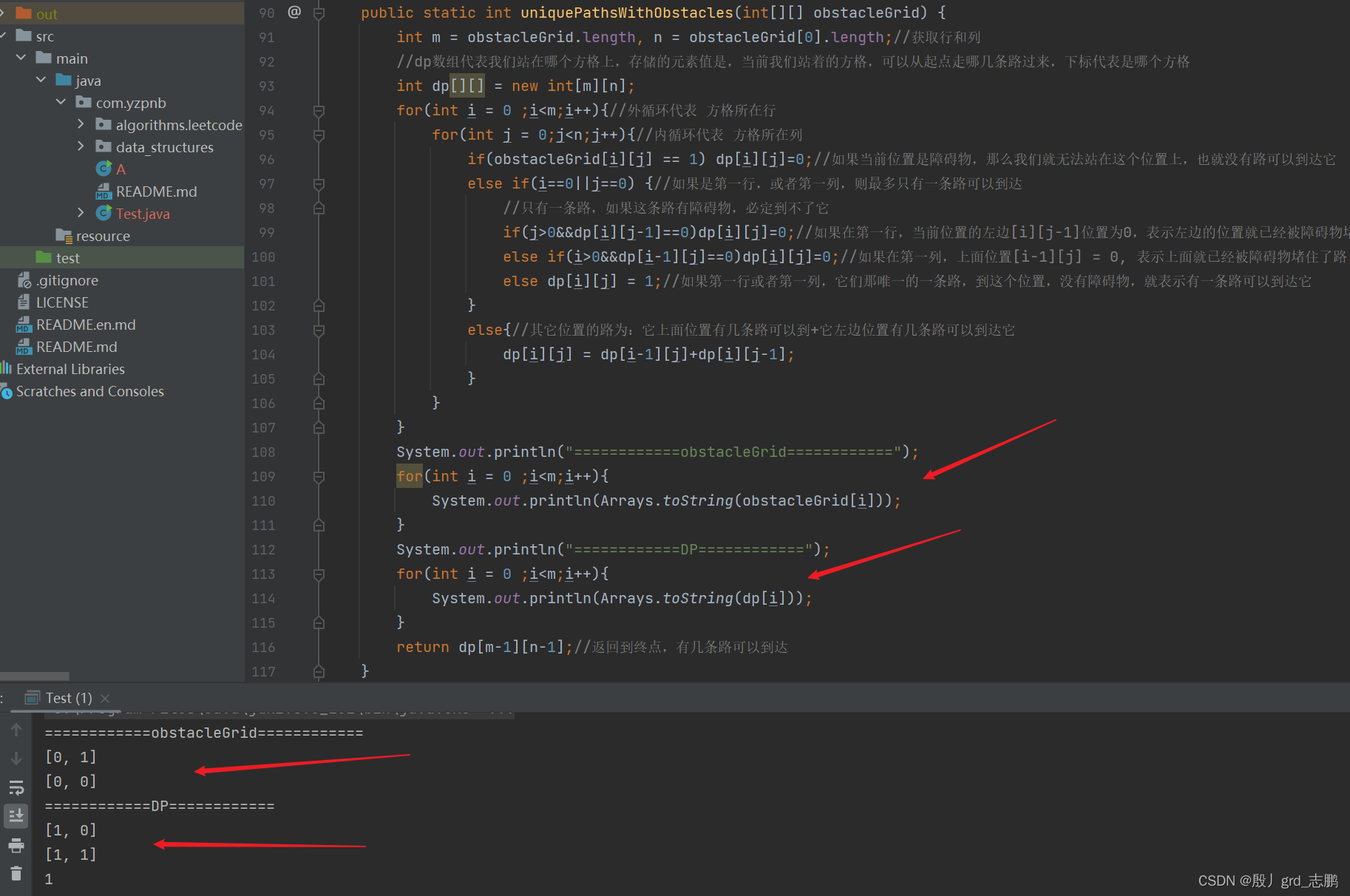
打印dp数组（自己生成dp数组后，将dp数组输出看看，是否和自己预想的一样。）

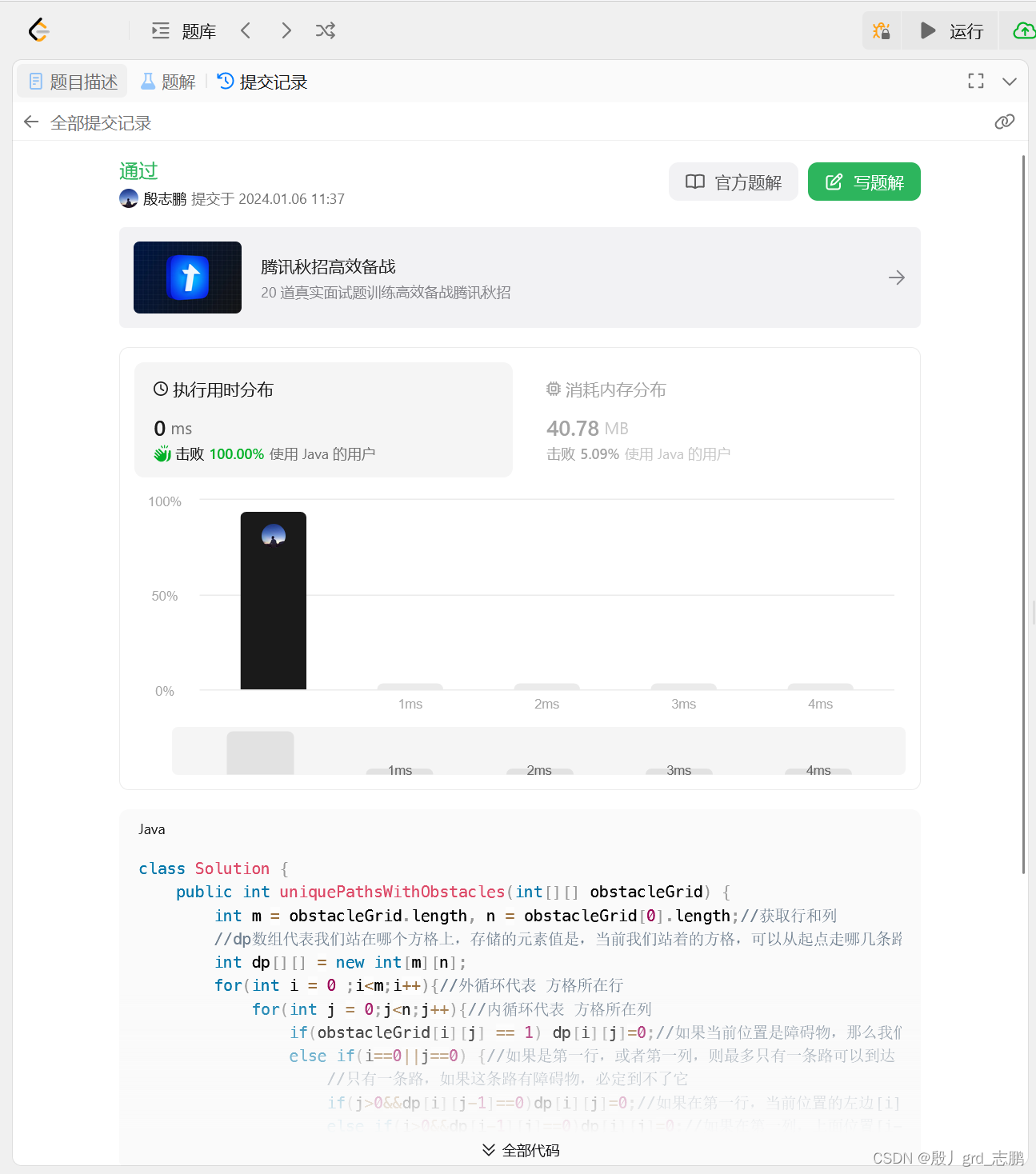
代码:时间复杂度O(mn).空间复杂度O(mn)

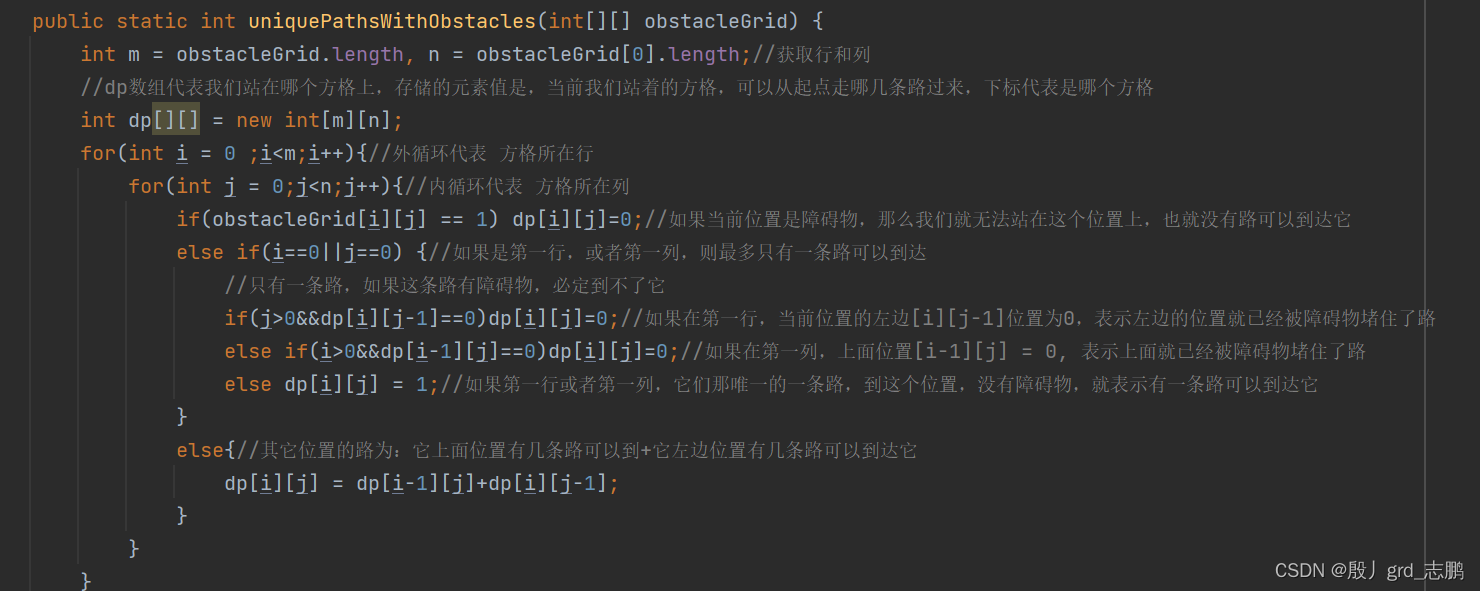
class Solution {
    public int uniquePathsWithObstacles(int[][] obstacleGrid) {
        int m = obstacleGrid.length, n = obstacleGrid[0].length;//获取行和列
        //dp数组代表我们站在哪个方格上，存储的元素值是，当前我们站着的方格，可以从起点走哪几条路过来，下标代表是哪个方格
        int dp[][] = new int[m][n];
        for(int i = 0 ;i<m;i++){//外循环代表 方格所在行
            for(int j = 0;j<n;j++){//内循环代表 方格所在列
                if(obstacleGrid[i][j] == 1) dp[i][j]=0;//如果当前位置是障碍物，那么我们就无法站在这个位置上，也就没有路可以到达它
                else if(i==0||j==0) {//如果是第一行，或者第一列，则最多只有一条路可以到达
                    //只有一条路，如果这条路有障碍物，必定到不了它
                    if(j>0&&dp[i][j-1]==0)dp[i][j]=0;//如果在第一行，当前位置的左边[i][j-1]位置为0，表示左边的位置就已经被障碍物堵住了路
                    else if(i>0&&dp[i-1][j]==0)dp[i][j]=0;//如果在第一列，上面位置[i-1][j] = 0, 表示上面就已经被障碍物堵住了路
                    else dp[i][j] = 1;//如果第一行或者第一列，它们那唯一的一条路，到这个位置，没有障碍物，就表示有一条路可以到达它
                }
                else{//其它位置的路为：它上面位置有几条路可以到+它左边位置有几条路可以到达它
                    dp[i][j] = dp[i-1][j]+dp[i][j-1];
                }
            }
        }
        return dp[m-1][n-1];//返回到终点，有几条路可以到达
    }
}