【数据结构】八大排序之快速排序算法

news2024/12/23 12:09:36

🦄个人主页:修修修也

🎏所属专栏:数据结构

⚙️操作环境:Visual Studio 2022

目录

一.快速排序简介及思路

二.快速排序代码实现的三种方式

📌左右交换法

📌挖坑填坑法

📌前后指针法

三.快速排序的时间复杂度分析

四.快速排序的优化

🎏优化选key方式

📌随机选key法

📌三数取中法

🎏小区间优化

📌小区间优化的原理

📌小区间优化的代码实现

五.借助栈实现非递归快速排序

📌为什么要将递归的快速排序算法改为非递归?

📌递归函数改非递归的思路

📌快速排序改非递归的思路

📌快速排序改非递归的代码实现

六.快速排序的三路划分

结语

一.快速排序简介及思想

快速排序(Quick Sort)是一种效率较高的交换排序算法.

它的基本思想是:

  • 通过一趟排序将待排数据分割成独立的两部分
  • 其中一部分数据的关键字均比另一部分数据的关键字小
  • 可分别对这两部分数据继续进行排序,以达到整个序列有序的目的.

算法动图演示:

二.快速排序代码实现的三种方式

我们了解了快速排序的基本思想是通过一趟排序将待排数据分割成独立的两部分之后,在代码的实现上,其实就有很多可以自由发挥的空间,如下较为主流的快速排序有三种实现思路,接下来我将一一带大家理解这三个思路并使用它们实现快排算法:

注:本文的快排实现思路均以升序为例!

📌左右交换法

左右交换法的思路是:

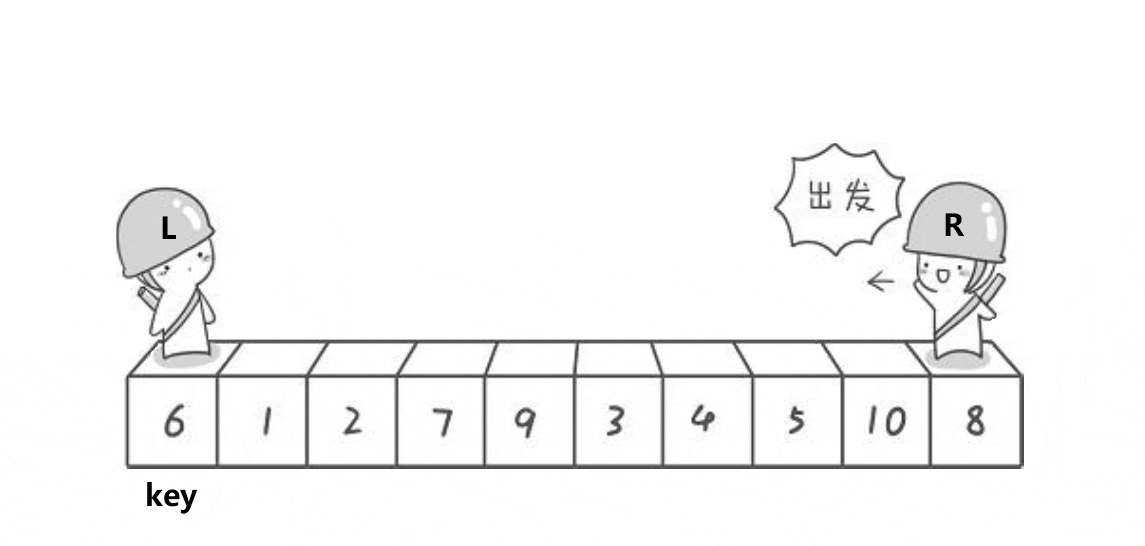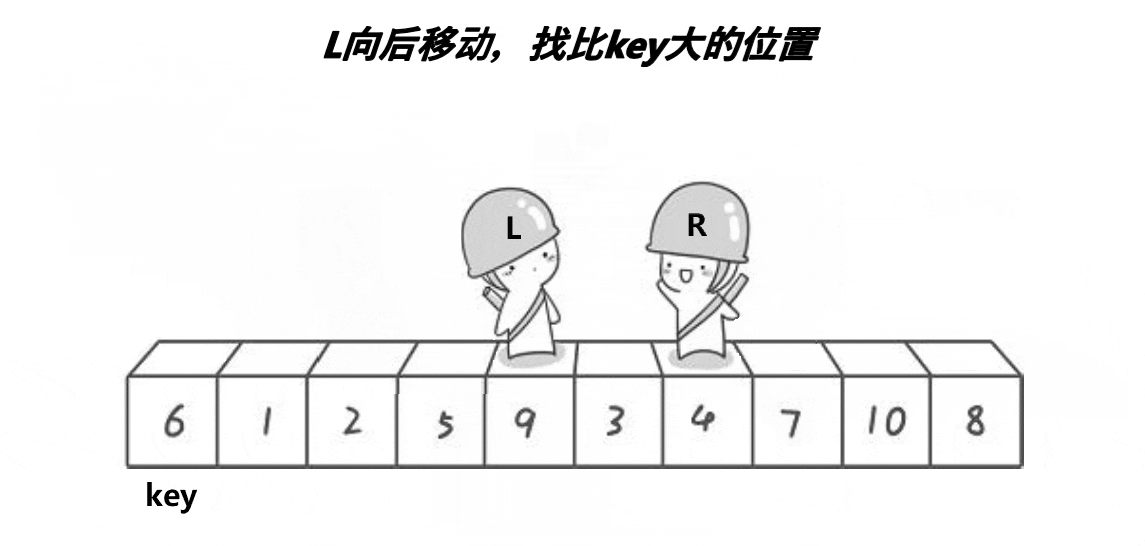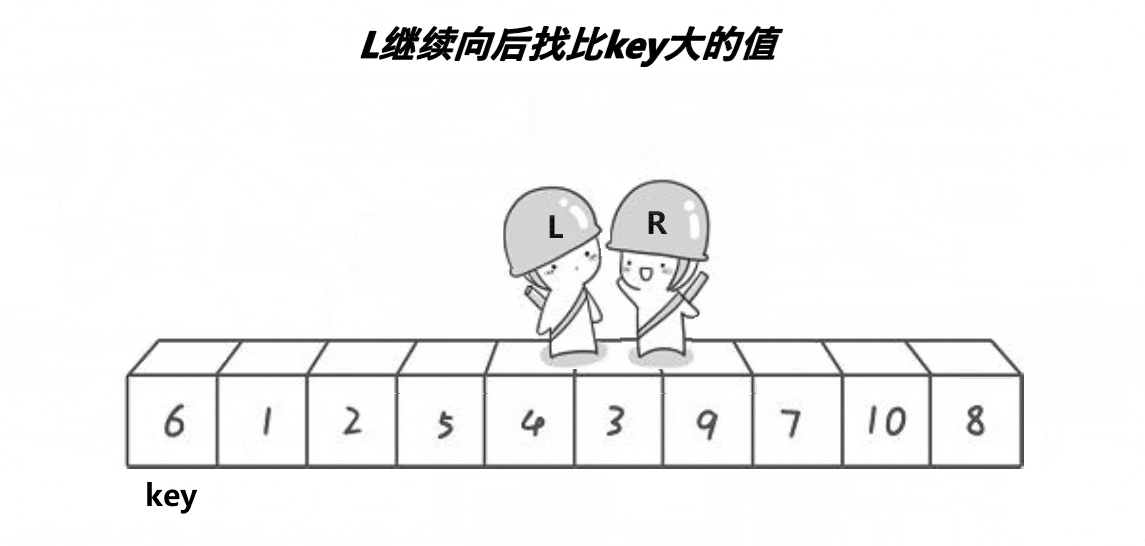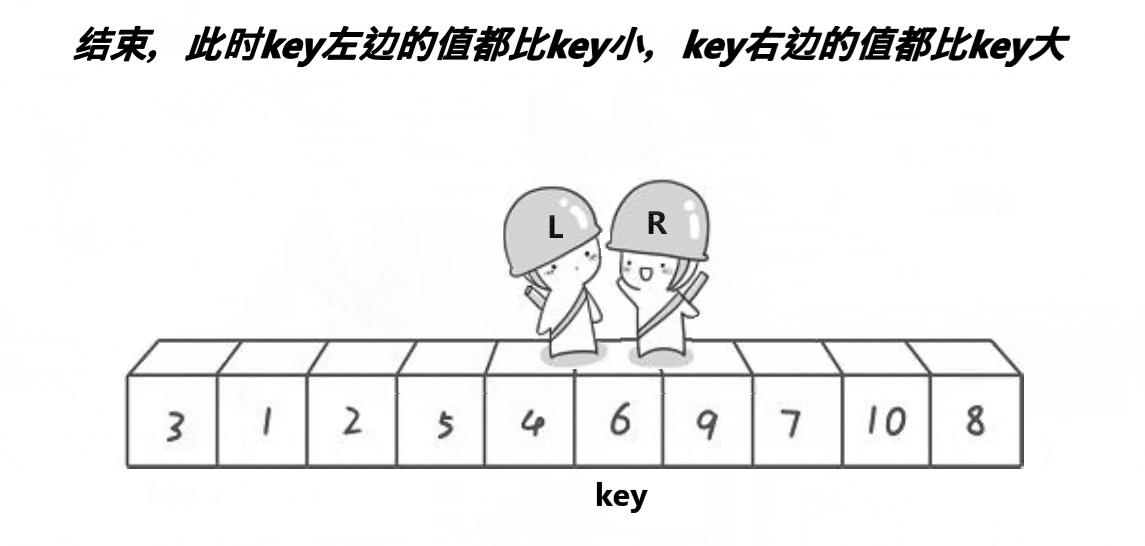
  1. 先选定当前待排序列的首元素位置的值为基准值(key).
  2. 然后设置一个右指针,使其从后向前遍历,找到比基准值(key)小的元素就停下来.
  3. 再设置一个左指针,使其从前向后遍历,找到比基准值(key)大的元素就停下来.
  4. 当左右指针都找到相应元素时,交换它们找到的元素.
  5. 重复步骤2~4,直到左右指针相遇
  6. 左右指针相遇后,将基准值(key)与相遇位置做交换,此时数组已经被重新一分为二成两个新的待排子序列.
  7. 分别继续对新的待排子序列继续执行步骤1~6排序,直到所有元素都排列在相应位置上为止.

左右交换法算法演示:

 清楚了左右交换法实现快排的思路后,我们编写实现代码就比较容易了,代码如下:

//交换函数
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

//快速排序(左右交换法
void QuickSort_swap(int* a, int left, int right)
{
	if (left >= right)
		return;
	int begin = left, end = right;

	int keyi = left;//选定序列首元素为基准值

	while (left < right)
	{
		//右边找小
		while (left < right && a[right] >= a[keyi])
			right--;
		//左边找大
		while (left < right && a[left] <= a[keyi])
			left++;
		//交换
		Swap(&a[left], &a[right]);
	}
	//相遇时交换key和相遇位置的值
	Swap(&a[keyi], &a[left]);

	keyi = left;//用keyi记录下本轮确定的基准值位置

	QuickSort_swap(a, begin, keyi - 1);//递归排序左区间[begin , keyi-1]
	QuickSort_swap(a, keyi + 1, end);//递归排序右区间[keyi+1 , end]
}

📌挖坑填坑法

挖坑填坑法是基于快排的基础思想提出的一种创新实现的思路,它的思路是这样的:

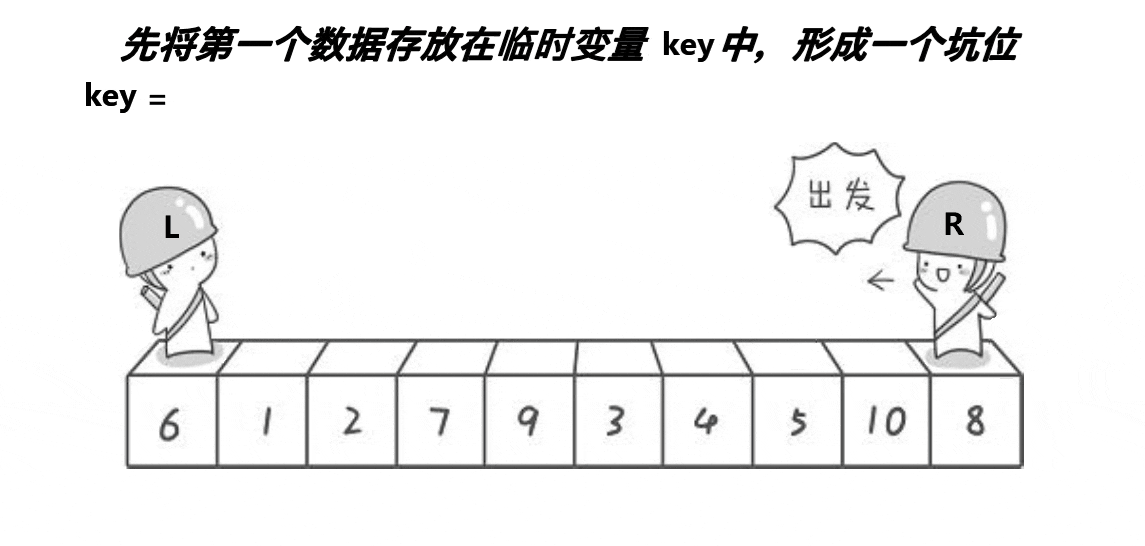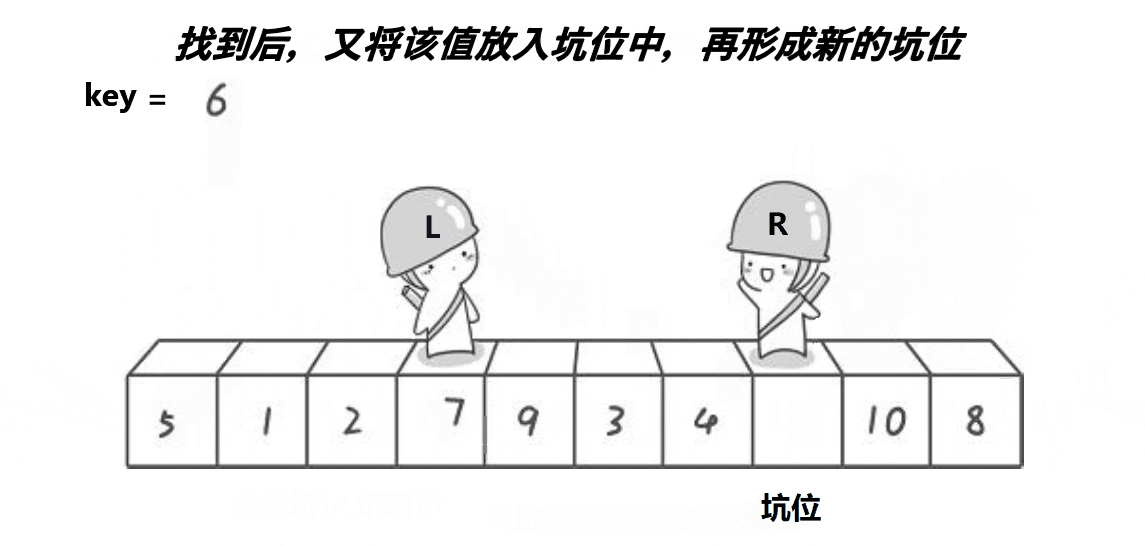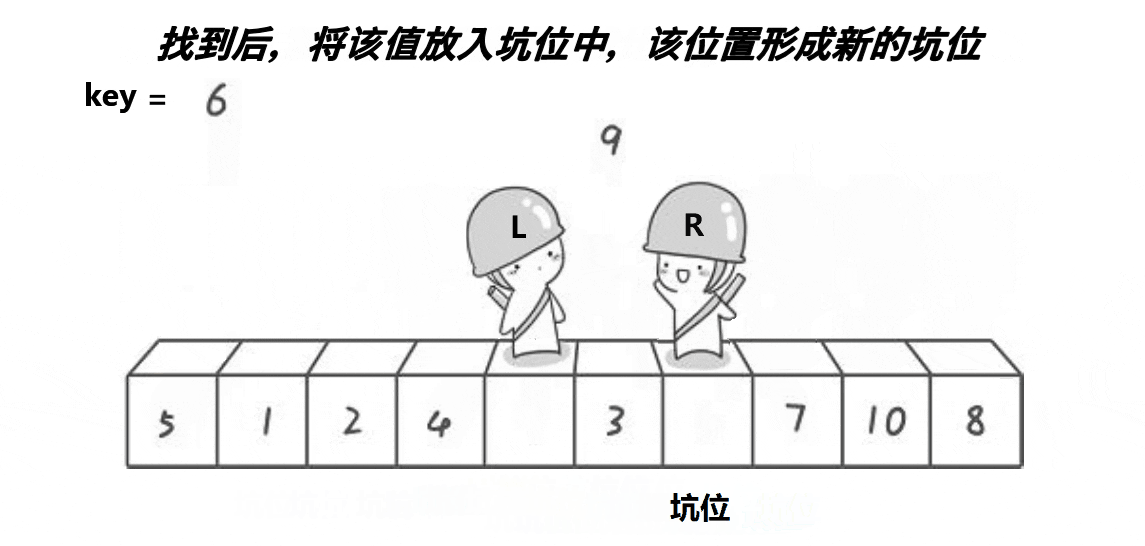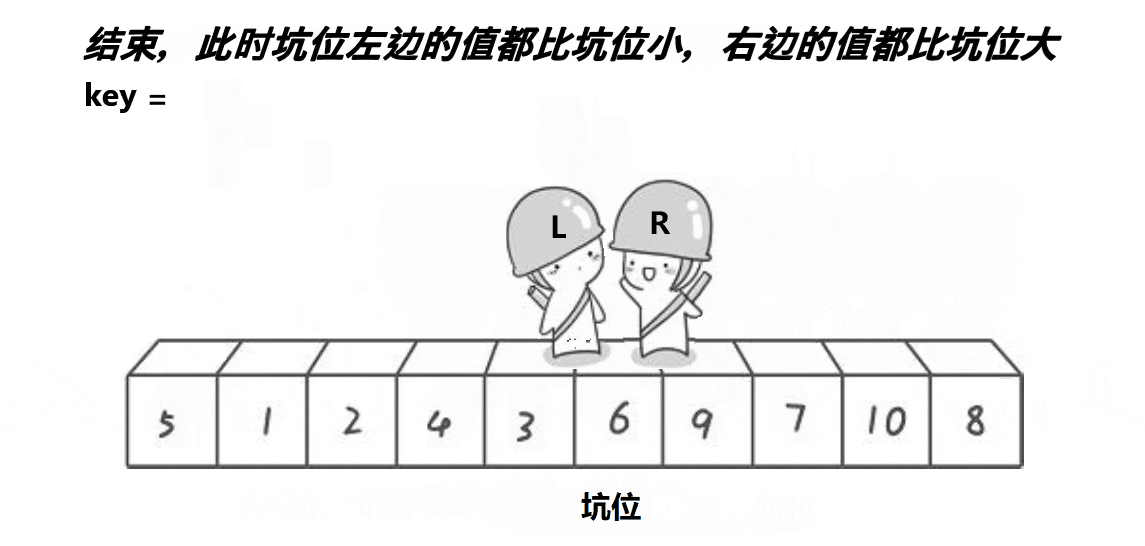
  1. 先记录下当前待排序列的首元素为基准值(key).
  2. 此时认为首元素的位置是空缺的,即该位置成为了一个坑.
  3. 设置一个右指针,使其从后向前遍历,找到比基准值(key)小的元素停下来将其填入刚才的坑位中,此时认为右指针找到的这个元素位置又形成了一个坑.
  4. 设置一个左指针,使其从前向后遍历,找到比基准值(key)大的元素停下来将其填入刚才的坑位中,此时认为左指针找到的这个元素位置又形成了一个坑.
  5. 左右指针不断向中间挪动不断填坑又形成新坑,直到两指针相遇
  6. 最后将基准值(key)填入左右指针相遇位置的坑中,此时数组已经被重新一分为二成两个新的待排子序列.
  7. 分别继续对新的待排子序列继续执行步骤1~6排序,直到所有元素都排列在相应位置上为止.

挖坑填坑法算法演示:

挖坑填坑法实现快排代码如下:

//快速排序(挖坑填坑法
void QuickSort_hole(int* a, int left, int right)
{
	if (left >= right)
		return;
	int begin = left, end = right;

	int key = a[left];//选定序列首元素为基准值,记录下基准值
	int hole = left;  //基准值的位置形成坑位

	while (left < right)
	{
		//右边找小
		while (left < right && a[right] >= key)
			right--;

		//找到了就填坑,更新坑
		a[hole] = a[right];
		hole = right;

		//左边找大
		while (left < right && a[left] <= key)
			left++;

		//找到了就填坑,更新坑
		a[hole] = a[left];
		hole = left;
	}

	//相遇时把key的值填进相遇的坑里
	a[hole] = key;

	QuickSort_hole(a, begin, hole - 1);//递归遍历左区间[begin , hole-1]
	QuickSort_hole(a, hole + 1, end);//递归遍历右区间[hole+1 , end]
}

📌前后指针法

前后指针法思路为:

  1. 先选定当前待排序列的首元素位置的值为基准值(key).
  2. 设立前指针prev,使其指向序列开头,即基准值位置
  3. 设立后指针cur,使其指向prev指针的后一个位置
  4. 判断cur指向的数据是否小于key:如果小于,则prev后移一位,然后将cur指向的内容与prev指向的内容交换, 然后cur指针++;如果不小于,则cur++.
  5. 循环步骤4,直到cur移动到超出序列范围时,交换prev位置和基准位置的值,此时数组已经被重新一分为二成两个新的待排子序列.
  6. 分别继续对新的待排子序列继续执行步骤1~5排序,直到所有元素都排列在相应位置上为止.

前后指针法算法演示:

前后指针法实现快排代码如下:

//交换
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

//快速排序(前后指针法
void QuickSort_follow(int* a, int left, int right)
{
	if (left >= right)
		return;
	int begin = left, end = right;

	int keyi = left;//选定序列首元素为基准值,记录下基准值位置

	int prev = left;
	int cur = prev + 1;

	while (cur <= right) //cur没有越界就继续
	{
		if (a[cur] < a[keyi] && ++prev != cur) //如果cur指向的值小于key,并且++prev与cur不重叠
		{
			Swap(&a[cur], &a[prev]);  //就交换它们
		}
		cur++; 
	}

	Swap(&a[prev], &a[keyi]);//交换prev和key的值
	keyi = prev;

	QuickSort_follow(a, begin, keyi - 1);//递归遍历左区间[begin , keyi-1]
	QuickSort_follow(a, keyi + 1, end);//递归遍历右区间[keyi+1 , end]
}

三.快速排序的时间复杂度分析

"快速排序的平均时间为 T_{avg}(n)=knlog_2n,其中n为待排序序列中数据的个数,k为某个常数,经验证明,在所有同数量级的此类(先进的)排序算法中,快速排序的常数因子k最小.因此,就平均时间而言,快速排序是目前被认为最好的一种内部排序方法.

通常,快速排序被认为是,在所有同数量级(O(nlogn))的排序算法中,其平均性能最好.但是,若初始数据序列按关键字有序或基本有序时,快速排序将蜕化为冒泡排序,其时间复杂度为O(n^2)."

                                ——《数据结构》严蔚敏

也就是说,快排的时间复杂度我们可以认为是O(nlogn),但当遇到原数组本身有序的情况下,其时间复杂度就会退化至O(n^2),这个其实很好理解,举个例子就明白了:

当最优情况下,即每趟选择key时都恰好选择到数组的中间值时(第n层可以确定2^{n-1}个数字位置),快排的时间复杂度如下图完全(满)二叉树:

该树每层需要遍历一遍数组,时间复杂度为n,而树高为h=log_2n,因此最优状态下快排的时间复杂度仅为O(nlogn).

而最坏情况下,即每趟选择key时都恰好选择到数组最大或最小的值时(即每一层都只能确定一个数字位置),快排的时间复杂度如下单支树:

该树每层遍历一遍数组,时间复杂度为n,而树高也为n,因此最坏状态下快排的时间复杂度为O(n^2).

综上,对快排时间复杂度的分析,我们不光理解了为什么快排排先天有序的数组时反而效率最差,同样也为我们后续对快排算法的优化提供了思路.

四.快速排序的优化

🎏优化选key方式

既然在快排在面对原本就接近有序的数组时排序会因为key值的选取导致效率降低,那么我们不妨优化一下我们快排时选key的方式,下面为大家介绍两种常用的优化选key的方式:

📌随机选key法

随机选key的思路为:

  1. 先使用rand()函数随机选出一个在[left,right]范围内的下标值randi
  2. 将randi下标的数据和keyi下标的数据互换

随机选key函数的实现:

//随机选key法
void SwapRand_key(int* a,int left, int right)
{
     int randi = left + (rand() % (right - left));
	 Swap(&a[left], &a[randi]);
}

结合随机选key法实现快排

我们写好随机选key函数后只需要在正常快排函数中选定keyi后(如下函数的第15行后)调用一下随机选keyi函数就可以将随机选出的key值和原本的key值做交换了.

实现代码如下:

//随机选key法
void SwapRand_key(int* a,int left, int right)
{
     int randi = left + (rand() % (right - left));
	 Swap(&a[left], &a[randi]);
}

//快速排序(前后指针法
void QuickSort_follow(int* a, int left, int right)
{
	if (left >= right)
		return;
	int begin = left, end = right;

	int keyi = left;    //选定序列首元素为基准值,记录下基准值

	SwapRand_key(a,left, right);  //随机选出一个数据交换基准值key
	
	int prev = left;
	int cur = prev + 1;

	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	keyi = prev;

	QuickSort_follow(a, begin, keyi - 1);//递归遍历左区间[begin , keyi-1]
	QuickSort_follow(a, keyi + 1, end);//递归遍历右区间[keyi+1 , end]
}

📌三数取中法

三数取中法的思路是:

  1. 比较序列首元素,尾元素,中间元素,取三者中的中间值作为midi
  2. 将midi下标的数据和keyi下标的数据互换

三数取中函数的实现:

//三数取中法
void SwapMid_key(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			midi = midi;
		}
		else if (a[left] > a[right])
		{
			midi = left;
		}
		else 
		{
			midi = right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[midi] > a[right])
		{
			midi = midi;
		}
		else if (a[left] < a[right])
		{
			midi = left;
		}
		else
		{
			midi = right;
		}
	}

	if (midi != left)
		Swap(&a[midi], &a[left]);
}

结合三数取中法实现快排

我们写好三数取中函数后只需要在正常快排函数中选定keyi后(如下函数的第45行后)调用一下三数取中函数就可以将三数取中选出的key值和原本的key值做交换了.

实现代码如下:

//三数取中函数
void SwapMid_key(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			midi = midi;
		}
		else if (a[left] > a[right])
		{
			midi = left;
		}
		else 
		{
			midi = right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[midi] > a[right])
		{
			midi = midi;
		}
		else if (a[left] < a[right])
		{
			midi = left;
		}
		else
		{
			midi = right;
		}
	}
	if (midi != left)
		Swap(&a[midi], &a[left]);
}

//快速排序(前后指针法
void QuickSort_follow(int* a, int left, int right)
{
	if (left >= right)
		return;
	int begin = left, end = right;

	int keyi = left;    //选定序列首元素为基准值,记录下基准值

	SwapMid_key(a, left, right);   //三数取中法选出基准值后交换基准值

	int prev = left;
	int cur = prev + 1;

	while (cur <= right)
	{
		if (a[cur] < a[keyi] && ++prev != cur)
		{
			Swap(&a[cur], &a[prev]);
		}
		cur++;
	}
	Swap(&a[prev], &a[keyi]);
	keyi = prev;

	QuickSort_follow(a, begin, keyi - 1);//递归遍历左区间[begin , keyi-1]
	QuickSort_follow(a, keyi + 1, end);//递归遍历右区间[keyi+1 , end]
}

🎏小区间优化

📌小区间优化的原理

快排的递归展开思路类似于二叉树,因此它们拥有同样的弊病,就是越靠近树的底部,空递归的情况就越多,并且空递归的规模量非常大,拿下面这颗树来举例:

我们递归遍历该树,发现空递归(紫色)访问次数竟然和总有效访问次数(绿色)是相同的.而对于快排来说,这样的空递归不仅浪费时间,而且是没有任何实际意义的.

因此我们可以考虑采用一种办法,将快排的递归范围加以限制,比如当我们不断分割快排子区间,当子区间数组元素小于10个数时,我们就不再进行快排递归排序,而使用直接插入排序来对该小区间进行排序,这样就可以有效的消灭超过一半的递归,从而提升快排的效率.

📌小区间优化的代码实现

清楚了上面的原理之后,我们实现小区间优化的思路为:

  1. 判断小区间数组是否小于10个数.
  2. 如果区间不小于10,则执行快排逻辑.
  3. 如果区间小于等于10,则执行直接插入排序逻辑.

综上所述,小区间代码实现如下:

//交换函数
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

//三数取中法取key函数
void SwapMid_key(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			midi = midi;
		}
		else if (a[left] > a[right])
		{
			midi = left;
		}
		else 
		{
			midi = right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[midi] > a[right])
		{
			midi = midi;
		}
		else if (a[left] < a[right])
		{
			midi = left;
		}
		else
		{
			midi = right;
		}
	}
	if (midi != left)
		Swap(&a[midi], &a[left]);
}

//直接插入排序函数
void InsertSort(int* a, int n)
{
	for (int i = 1; i < n; i++)
	{
		int end = i - 1;
		int tmp = a[i];
		//将tmp插入到[0,end]这个区间里
		while (end >= 0)
		{
			if (tmp < a[end])
			{
				a[end + 1] = a[end];
				end--;
			}
			else
			{
				break;
			}
		}
		a[end + 1] = tmp;
	}
}

//小区间优化版快排
void QuickSort(int* a, int left, int right)
{
	if (left >= right)
		return;
	if ((right - left + 1 ) > 10)
	{
		int keyi = left;
		SwapMid_key(a, left, right);

		//双指针前后移动法快排
		int prev = left;
		int cur = left + 1;
		while (cur <= right)
		{
			if (a[cur] < a[keyi] && ++prev != cur)
				Swap(&a[cur], &a[prev]);

			++cur;
		}
		Swap(&a[prev], &a[keyi]);
		keyi = prev;

		QuickSort(a, left, keyi - 1);
		QuickSort(a, keyi + 1, right);
	}
	else
	{
		InsertSort( a + left , right - left + 1 );
	}
}

五.借助栈实现非递归快速排序

📌为什么要将递归的快速排序算法改为非递归?

递归函数有以下几个缺点:

  • 内存消耗大：递归调用会占用大量的内存空间，因为每次调用都需要在内存中保存当前的状态和参数。

  • 性能低下：递归调用会增加函数调用的开销，因此在一些情况下会导致程序的性能下降。

  • 可读性差：递归函数通常比较复杂，难以理解和调试，降低了代码的可读性。

  • 可能导致栈溢出：如果递归调用层次过深，会导致栈溢出的问题，使程序崩溃。

  • 难以优化：一些编译器和优化工具难以对递归函数进行有效的优化，导致性能不佳。

📌递归函数改非递归的思路

  1. 直接改为循环.(如:斐波那契数列)
  2. 利用栈辅助改为循环.(如:二叉树的前序遍历)

📌快速排序改非递归的思路

  1. 将初始数组区间压入栈
  2. 在栈里取一段区间,单趟排序
  3. 单趟分割子区间入栈
  4. 子区间只有一个值或着不存在就不入栈
  5. 重复步骤2-4,直到栈为空,则排序完成.

📌快速排序改非递归的代码实现

因为快排改非递归时要借助栈结构,因此我先将栈相关定义的头文件贴在这里,具体栈的C语言完整实现可以移步我的另一篇博客,在文末有数据结构栈实现的完整代码,大家可以直接粘贴过来使用:

【数据结构】C语言实现顺序栈(附完整运行代码)icon-default.png?t=N7T8http://t.csdnimg.cn/FL0V3(注:如果本身没有自己实现数据结构栈的工程文件的,一定要将该博客末尾的Stack.h文件和Stack.c文件粘贴在排序项目文件里才可以正常使用栈的相关功能,否则C语言是不支持直接使用的!)

#define _CRT_SECURE_NO_WARNINGS 1
#include<stdio.h>
#include<stdlib.h>
#include<stdbool.h>
#include<assert.h>

typedef int STDataType;

typedef struct Stack
{
	STDataType*arr;
	int top;
	int capacity;
}ST;

void STInit(ST* ps);
void STDestroy(ST* ps);
void STPush(ST* ps, STDataType x);
void STPop(ST* ps);
int STSize(ST* ps);
bool STEmpty(ST* ps);
STDataType STTop(ST* ps);
void STMenu();

综上,快排的非递归代码实现如下:

//交换函数
void Swap(int* a, int* b)
{
	int tmp = *a;
	*a = *b;
	*b = tmp;
}

//三数取中法取key函数
void SwapMid_key(int* a, int left, int right)
{
	int midi = (left + right) / 2;
	if (a[left] < a[midi])
	{
		if (a[midi] < a[right])
		{
			midi = midi;
		}
		else if (a[left] > a[right])
		{
			midi = left;
		}
		else 
		{
			midi = right;
		}
	}
	else // a[left] > a[mid]
	{
		if (a[midi] > a[right])
		{
			midi = midi;
		}
		else if (a[left] < a[right])
		{
			midi = left;
		}
		else
		{
			midi = right;
		}
	}
	if (midi != left)
		Swap(&a[midi], &a[left]);
}

//快速排序主函数(非递归版
void QuickSortNonR(int* a, int left, int right)
{
	ST st;
	STInit(&st);

	STPush(&st, right);//先入后出
	STPush(&st, left);

	while (!STEmpty(&st))
	{
		int begin = STTop(&st);
		STPop(&st);
		int end = STTop(&st);
		STPop(&st);

		int keyi = begin;
		SwapMid_key(a, begin, end);

		//双指针前后移动法快排
		int prev = begin;
		int cur = begin + 1;

		while (cur <= end)
		{
			if (a[cur] < a[keyi] && ++prev != cur)
				Swap(&a[cur], &a[prev]);
			++cur;
		}

		Swap(&a[prev], &a[keyi]);
		keyi = prev;

		if (keyi + 1 < end)
		{
			STPush(&st, end);
			STPush(&st, keyi + 1);
		}

		if (begin < keyi - 1)
		{
			STPush(&st, keyi - 1);
			STPush(&st, begin);
		}
	}

	STDestroy(&st);
}

六.快速排序的三路划分

//主要解决快速排序面对大量重复数据时效率低下的问题

//该部分内容待补

结语

希望这篇快速排序算法详解能对大家有所帮助,欢迎大佬们留言或私信与我交流.

有关更多排序相关知识可以移步:

【数据结构】八大排序算法​​icon-default.png?t=N7T8https://blog.csdn.net/weixin_72357342/article/details/135038495?csdn_share_tail=%7B%22type%22%3A%22blog%22%2C%22rType%22%3A%22article%22%2C%22rId%22%3A%22135038495%22%2C%22source%22%3A%22weixin_72357342%22%7D&fromshare=blogdetail

学海漫浩浩,我亦苦作舟!关注我,大家一起学习,一起进步!

相关文章推荐

【数据结构】八大排序之冒泡排序算法

【数据结构】八大排序之希尔排序算法

【数据结构】八大排序之直接插入排序算法

【数据结构】八大排序之简单选择排序

【数据结构】八大排序之堆排序算法

 数据结构排序篇思维导图:

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1361393.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MvvmToolkit的使用

MvvmToolkit的使用

背景&#xff1a;MvvmLight不更新了&#xff0c;用Toolkit代替 1、首先下载好社区版本的NuGet包 2、ViewModel中需要继承ObservableObject&#xff0c;查看ObservableObject可以看到里面有实现好InotifyPropertyChanged。 3、对于属性的set&#xff0c;可以简写成一行&#xff…
阅读更多...
网络名称解读 -入门5

网络名称解读 -入门5

WAN: Wide Area Network(跨区域&#xff09;&#xff0c;LAN&#xff1a; Local Area NetworkWAN MAC&#xff0c; 用来连接上级网络&#xff0c; LAN MAC&#xff0c; 用于内部网路。 LAN & WAN 3.1&#xff0c;LAN表示子网&#xff0c;通过掩码来筛选子网内主机数量&…
阅读更多...
【动态规划】【字符串】C++算法：140单词拆分

【动态规划】【字符串】C++算法：140单词拆分

作者推荐 【动态规划】【字符串】扰乱字符串 本文涉及的基础知识点 动态规划 字符串 LeetCode140:单词拆分 II 给定一个字符串 s 和一个字符串字典 wordDict &#xff0c;在字符串 s 中增加空格来构建一个句子&#xff0c;使得句子中所有的单词都在词典中。以任意顺序 返回…
阅读更多...
创建专业电子邮件签名：提升个人与品牌形象的实用指南

创建专业电子邮件签名：提升个人与品牌形象的实用指南

电子邮件签名乃是品牌建设中常被忽略的一环。试想一下&#xff0c;若名片只是普通的、手工切割的复印纸&#xff0c;上面用黑体打印着你的联系方式&#xff0c;那将是多么平凡无奇。这将显得廉价、乏味且不专业——这正是人们不愿如此的原因。相反&#xff0c;他们渴望让自己的…
阅读更多...
MySQL-DDL

MySQL-DDL

DDL是数据定义语言&#xff0c;用来定义数据对象&#xff08;数据库&#xff0c;表&#xff0c;字段&#xff09; 数据库操作&#xff1a; 1.查询&#xff1a; 查询所有数据库&#xff1a;SHOW DATABASES; 查询当前数据库&#xff1a;SELECT DATABASE(); 2.创建&#xff1a; C…
阅读更多...
彻底解决vue-video-player视频铺满div

彻底解决vue-video-player视频铺满div

需求 最近需要接入海康视频摄像头&#xff0c;然后把视频的画面接入到自己的网站系统中。以前对接过rtsp固定IP的显示视频&#xff0c;这次的不一样&#xff0c;没有了固定IP。海康的解决办法是&#xff0c;摄像头通过配置服务器到萤石云平台&#xff0c;然后购买企业版账号和…
阅读更多...
编程语言的未来？直观点5年之际！

编程语言的未来？直观点5年之际！

编程语言的未来&#xff1f;未来5年应该如何发展&#xff01; 随着科技的飞速发展&#xff0c;编程语言在计算机领域中扮演着至关重要的角色。它们是软件开发的核心&#xff0c;为程序员提供了与机器沟通的桥梁。那么&#xff0c;在技术不断进步的未来&#xff0c;编程语言的走…
阅读更多...
selenium实现UI自动化

selenium实现UI自动化

1.selenium简介 selenium是支持web浏览器自动化的一系列工具和库的综合项目。具有支持linux、windows等多个平台&#xff0c;支持Firefox、chrome等多种主流浏览器&#xff1b;支持Java、Python等多种语言。 主要包括的三大工具有&#xff1a; WebDriver&#xff08;rc 1.0)、…
阅读更多...
优雅永不过时: spring-retry 重试框架

优雅永不过时: spring-retry 重试框架

文章目录 前言一、幂等性是重试的前提二、使用步骤1.引入依赖2.启动类或配置类上添加EnableRetry,启用retry框架3.创建一个要重试的方法4.自定义一个retry监听5.创建一个测试类 总结 前言 Spring Retry 是一个用于在 Spring 应用中实现重试机制的库。它提供了一种方便的方式来…
阅读更多...
AOP(面向切面编程)基于XML方式配置

AOP(面向切面编程)基于XML方式配置

概念解释&#xff1a;&#xff08;理解基本概念方可快速入手&#xff09; 连接点&#xff08;joinpoint&#xff09; 被拦截到的点&#xff0c;因为Spring只支持方法类型的连接点&#xff0c;所以在Spring中连接点指的就是被拦截到的方法。 切入点&#xff08;pointcut&#x…
阅读更多...
在电商狂欢中，什么平台更加对商家有利？

在电商狂欢中，什么平台更加对商家有利？

我是电商珠珠 近年来&#xff0c;不管是直播电商也好&#xff0c;电商平台也好&#xff0c;都一直朝着向上走的趋势。 我做电商也已经有5年时间了&#xff0c;期间做过天猫&#xff0c;快手、抖店&#xff0c;团队从原来的几个人&#xff0c;扩大到了70。 在22年10月&#x…
阅读更多...
使用ObjectARX事务功能做小动画处理

使用ObjectARX事务功能做小动画处理

使用ObjectARX事务功能做小动画处理&#xff0c;可以用于几何算法调试等 void CmdFun::Test() {if (true){ads_point pt;ads_name en;if (RTNORM ! acedEntSel(_T("\n选中对象 : "), en, pt))return;AcDbObjectId id;if (Acad::eOk ! acdbGetObjectId(id, en))retur…
阅读更多...
哈尔滨爆火的背后有什么值得我们学习的，2024普通人如何创业/2024风口行业

哈尔滨爆火的背后有什么值得我们学习的，2024普通人如何创业/2024风口行业

这个冬天&#xff0c;“南方小土豆”带火东北冰雪游。“冰城”黑龙江哈尔滨的文旅市场异常火爆&#xff0c;元旦假期3天&#xff0c;哈尔滨市累计接待游客304.79万人次&#xff0c;实现旅游总收入59.14亿元。旅游总收入达到历史峰值。哈尔滨旅游怎么就爆火了&#xff1f;背后究…
阅读更多...
鸿蒙学习笔记

鸿蒙学习笔记

DevEco Studio, ArkTS, ArkUI, ArkCompiler, DevEco Testing是啥 DevEco Studio是华为开发的一款集成开发环境&#xff08;IDE&#xff09;&#xff0c;用于开发基于华为鸿蒙操作系统&#xff08;HarmonyOS&#xff09;的应用程序。它提供了丰富的开发工具和功能&#xff0c;包…
阅读更多...
Baumer工业相机堡盟工业相机如何通过NEOAPI SDK修改图像像素格式Mono8或者Mono10（C#）

Baumer工业相机堡盟工业相机如何通过NEOAPI SDK修改图像像素格式Mono8或者Mono10（C#）

Baumer工业相机堡盟工业相机如何通过NEOAPI SDK修改图像像素格式Mono8或者Mono10&#xff08;C#&#xff09; Baumer工业相机Baumer工业相机的图像像素格式的技术背景CameraExplorer如何查看修改相机图像像素格式信息在NEOAPI SDK里通过函数修改图像像素格式修改像素格式测试演…
阅读更多...
微信小程序启用组件按需注入

微信小程序启用组件按需注入

微信小程序在预览或上传的时候会进行代码质量检测&#xff0c;有时候会提示‘组件需按需注入’&#xff0c;如下图所示&#xff1a; 这是只要加一句代码"lazyCodeLoading": "requiredComponents" 就行了 &#xff0c;添加的位置在app.json文件的里面&#…
阅读更多...
【linux】lsblk和df -h显示的磁盘信息不同

【linux】lsblk和df -h显示的磁盘信息不同

【问题分析】 lsblk 查看的是block device,也就是逻辑磁盘大小。 df查看的是file system, 也就是文件系统层的磁盘大小。 这种情况应该是block device容量变大&#xff0c;单还没有反映到file system中。 【问题解决】 如果是ext{2,3,4}文件系统的话&#xff0c;可以用res…
阅读更多...
中断产生流程

中断产生流程

中断产生流程 中断向量表 entry.S (arch\arm64\kernel) ENTRY(vectors) kernel_ventry 1, sync_invalid // Synchronous EL1t kernel_ventry 1, irq_invalid // IRQ EL1t kernel_ventry 1, fiq_invalid // FIQ EL1t …
阅读更多...
linux中最常用的用户信息命令

linux中最常用的用户信息命令

文章目录 linux中最常用的用户信息命令还有谁 last语法一般使用方法查看最近登陆的三个用户省略hostname显示最后一列显示主机IP地址 我是谁 whoami谁&#xff1f;who默认使用系统的运行时间显示表头信息显示登录的人员及总数 什么&#xff1f;谁&#xff1f;w (who & what…
阅读更多...
如何理解Transformer论文中的positional encoding，和三角函数有什么关系？

如何理解Transformer论文中的positional encoding，和三角函数有什么关系？

大家好&#xff0c;我分享交流下这个问题。 Positional Encoding 掏出一张被无数人讲述的架构图。 Transformer 模型中的位置编码&#xff08;Positional Encoding&#xff09;是为了让模型能够考虑单词在句子中的位置。 由于 Transformer 的自注意力&#xff08;Self-Atte…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023